Question
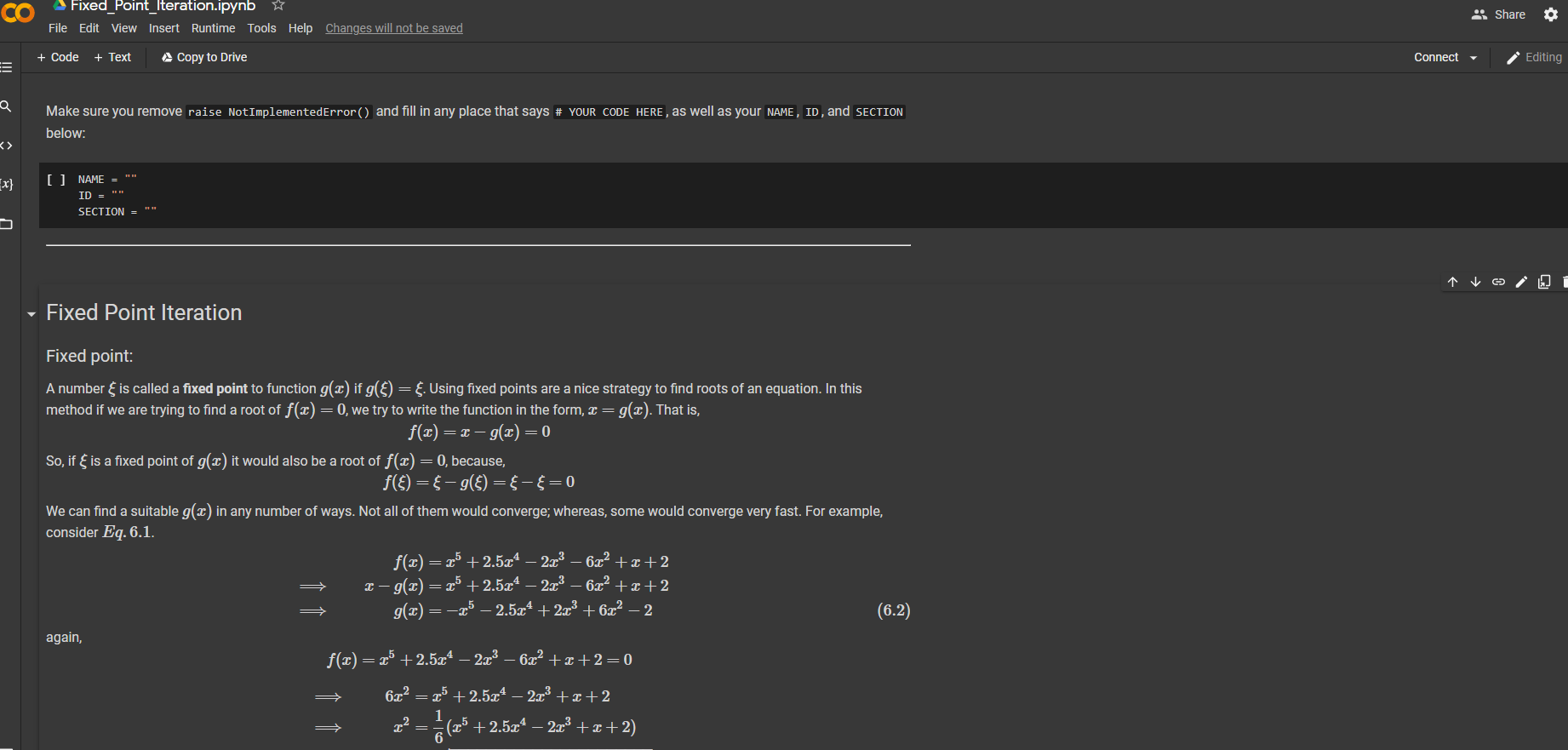
Make sure you remove raise NotImplementedError() and fill in any place that says # YOUR CODE HERE . Fixed Point Iteration Fixed point: A number
Make sure you remove raise NotImplementedError() and fill in any place that says # YOUR CODE HERE .
Fixed Point Iteration
Fixed point:
A number is called a fixed point to function g(x) if g()=. Using fixed points are a nice strategy to find roots of an equation. In this method if we are trying to find a root of f(x)=0, we try to write the function in the form, x=g(x). That is,
f(x)=xg(x)=0
So, if is a fixed point of g(x) it would also be a root of f(x)=0, because,
f()=g()==0
We can find a suitable g(x) in any number of ways. Not all of them would converge; whereas, some would converge very fast. For example, consider Eq.6.1.
f(x)xg(x)g(x)=x5+2.5x42x36x2+x+2=x5+2.5x42x36x2+x+2=x52.5x4+2x3+6x22(6.2)
again,
f(x)=x5+2.5x42x36x2+x+2=0
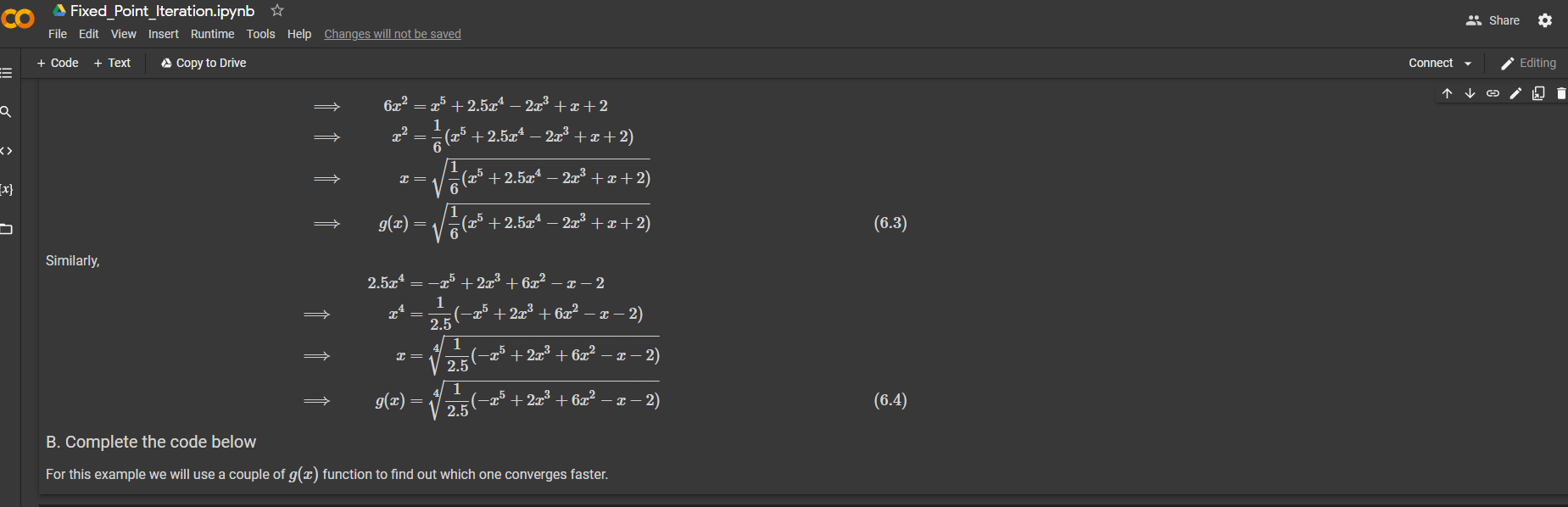
6x2x2xg(x)=x5+2.5x42x3+x+2=16(x5+2.5x42x3+x+2)=16(x5+2.5x42x3+x+2)=16(x5+2.5x42x3+x+2)(6.3)
Similarly,
2.5x4x4xg(x)=x5+2x3+6x2x2=12.5(x5+2x3+6x2x2)=12.5(x5+2x3+6x2x2)4=12.5(x5+2x3+6x2x2)4(6.4)
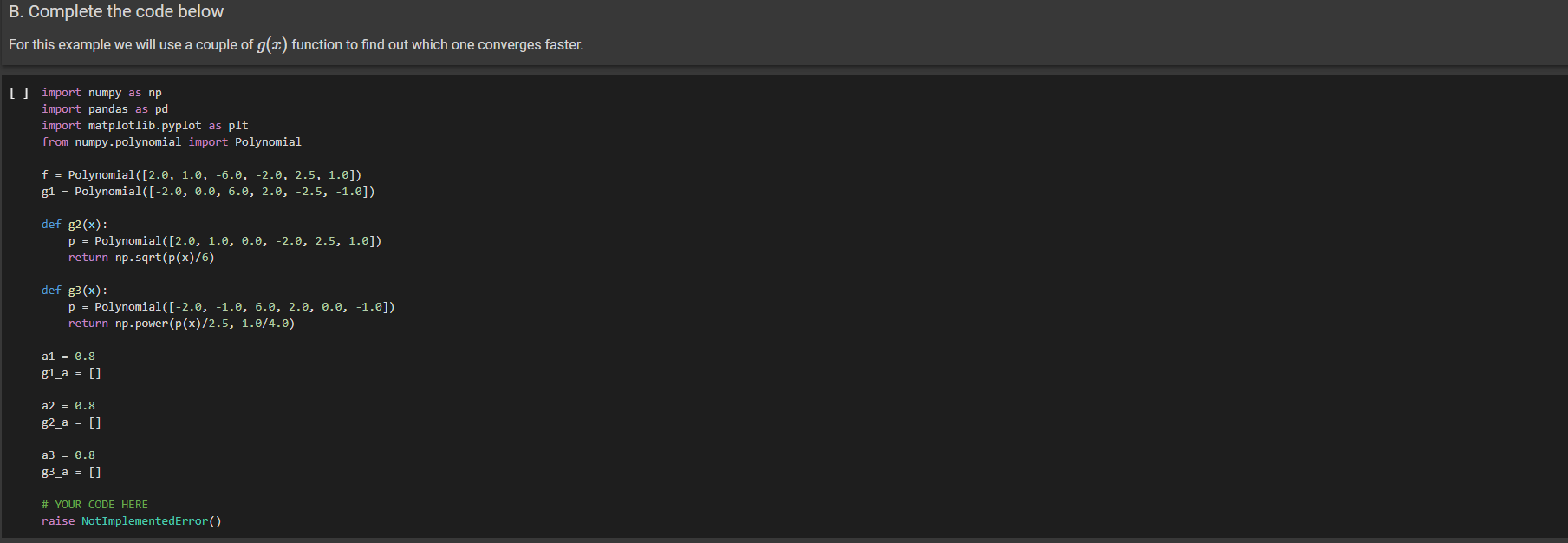
B. Complete the code below
For this example we will use a couple of g(x) function to find out which one converges faster.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from numpy.polynomial import Polynomial
f = Polynomial([2.0, 1.0, -6.0, -2.0, 2.5, 1.0])
g1 = Polynomial([-2.0, 0.0, 6.0, 2.0, -2.5, -1.0])
def g2(x):
p = Polynomial([2.0, 1.0, 0.0, -2.0, 2.5, 1.0])
return np.sqrt(p(x)/6)
def g3(x):
p = Polynomial([-2.0, -1.0, 6.0, 2.0, 0.0, -1.0])
return np.power(p(x)/2.5, 1.0/4.0)
a1 = 0.8
g1_a = []
a2 = 0.8
g2_a = []
a3 = 0.8
g3_a = []
# YOUR CODE HERE
raise NotImplementedError()
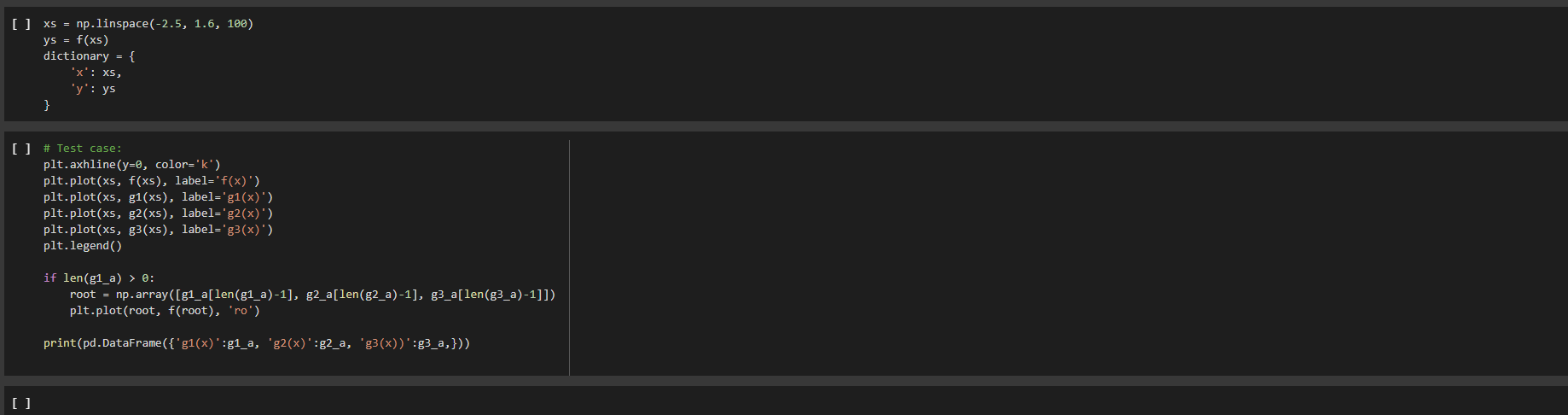
xs = np.linspace(-2.5, 1.6, 100)
ys = f(xs)
dictionary = {
'x': xs,
'y': ys
}
# Test case:
plt.axhline(y=0, color='k')
plt.plot(xs, f(xs), label='f(x)')
plt.plot(xs, g1(xs), label='g1(x)')
plt.plot(xs, g2(xs), label='g2(x)')
plt.plot(xs, g3(xs), label='g3(x)')
plt.legend()
if len(g1_a) > 0:
root = np.array([g1_a[len(g1_a)-1], g2_a[len(g2_a)-1], g3_a[len(g3_a)-1]])
plt.plot(root, f(root), 'ro')
print(pd.DataFrame({'g1(x)':g1_a, 'g2(x)':g2_a, 'g3(x))':g3_a,}))
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


