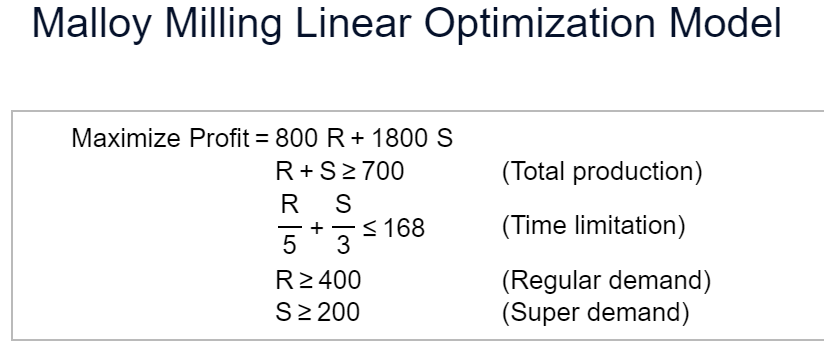
Malloy Milling grinds calcined alumina to a standard granular size. The mill produces two different size products, regular grind and super grind, from the same raw materials. After reviewing the production rate, demand, and profit for each of the two types of grind, Malloy Milling found the accompanying linear optimization model for profit, where R is the number of tons of regular grind produced and S is the number of tons of super grind produced. Implement the linear optimization model and find an optimal solution. Using the Solver Sensitivity Report, answer the following questions, explaining what information you used in the Sensitivity Report. Complete parts a through c.

Please complete the following 3 questions

Pleaseee answer, I will give give points!!

Malloy Milling Linear Optimization Model a. What impact will changing the required minimum number of tons per week (currently 700 ) have on the solution? Since the shadow price is increasing the minimum number of tons per week will profits, while decreasing the minimum number of tons per week will profits. b. If the price per ton for regular grind is increased to $850, how will the solution be affected? b. If the price per ton for regular grind is increased to $850, how will the solution be affected? A. The optimal solution and profit could both change. The new profit would be $. (Round to the nearest dollar as needed.) B. The optimal solution would not change. The profit would change to $. (Round to the nearest dollar as needed.) C. The optimal solution would not change. The profit would not change. c. If the price per ton for super grind is decreased to $1200 because of low demand, how will the solution change? A. The optimal solution and profit could both change. The new profit would be $. (Round to the nearest dollar as needed.) B. The optimal solution would not change. The profit would change to $. (Round to the nearest dollar as needed.) C. The optimal solution would not change. The profit would not change. Malloy Milling Linear Optimization Model a. What impact will changing the required minimum number of tons per week (currently 700 ) have on the solution? Since the shadow price is increasing the minimum number of tons per week will profits, while decreasing the minimum number of tons per week will profits. b. If the price per ton for regular grind is increased to $850, how will the solution be affected? b. If the price per ton for regular grind is increased to $850, how will the solution be affected? A. The optimal solution and profit could both change. The new profit would be $. (Round to the nearest dollar as needed.) B. The optimal solution would not change. The profit would change to $. (Round to the nearest dollar as needed.) C. The optimal solution would not change. The profit would not change. c. If the price per ton for super grind is decreased to $1200 because of low demand, how will the solution change? A. The optimal solution and profit could both change. The new profit would be $. (Round to the nearest dollar as needed.) B. The optimal solution would not change. The profit would change to $. (Round to the nearest dollar as needed.) C. The optimal solution would not change. The profit would not change