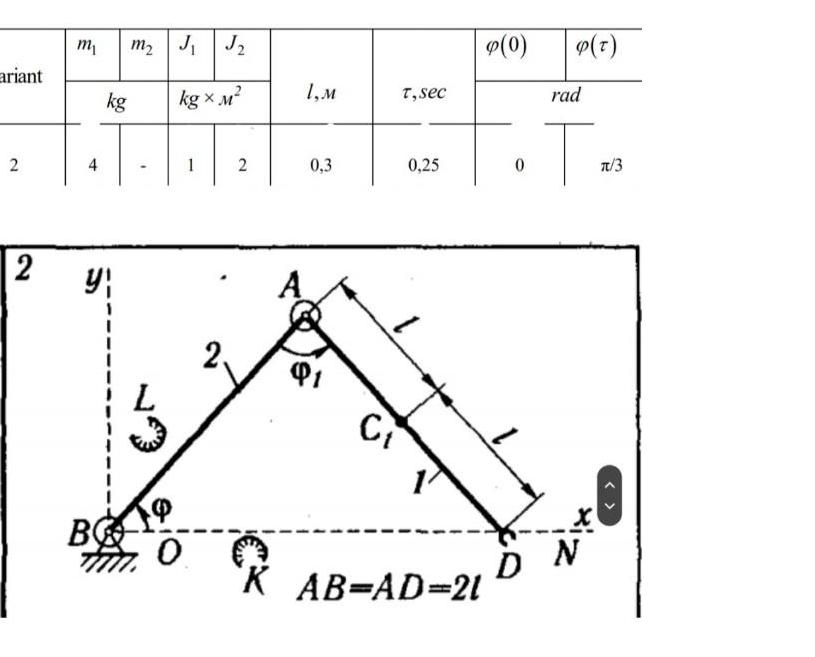
Manipulator (Fig. 8.3), which consists of the links 1, 2 and capture D is driven by actuators A and B. Capture D moves along the straight line ON. There is a control torque M (variants 2, 4, 7, 8, 12, 22, 24-26, 29), or force P, (variants 1, 3, 5, 6, 9-1, 13-21, 23, 27, 28, 30) acting from the drive A to the link 1. The drive B acts on the link 2 with a torque MB (variants 1-3, 5b, 8-11, 13-21, 23, 27) or with a control force P (variants 4, 7, 12, 22, 24-26, 28-30). Motion of the link 1 (variants 3, 4, 7, 12, 22, 24-26, 28-30) or link 2 (variants 1, 2, 5, 6, 8-11, 13-21, 23, 27) is limited by some restrictions K and L, so changing the angle of rotation of this link is possible only within the range of [po), p(r)], where r-time of the motion of the link. Technical operating conditions of the manipulator require that the specified link went off the restriction K at 1=0 and "softly" touched restriction L when t-r, so that the following conditions have to be satisfied: (1)-03- = 0; t=0J=r 29 = 0. - the mass of the second link; Program motion of the link 1, satisfying the requirements of the "soft" touch, is taken in the form: 1)p(t)=p(0) +[p(z) - p(0)](10-15t/r+61/t)3 / 7 (variants 2, 4,6,7,11,12,16,19,22,24-26,28-30); 2)p(t)=P(0) +[p(t)-p(0)][t/t-(1/(2x)) sin(2rt / T)](variants 1, 3,5,8-10,13-15,17,18,20,21,23,27). The values of (0) and o(r) are given in the Table. 8.1. Neglect forces of resistance. The mechanism is in a horizontal plane. Neglect the motion of a capture relatively link 1. The following notations are used in the problem: m, the mass of the first link, the capture and the object transferred in a capture; m J moment of inertia of the link 1, capture and object transferred by the capture relative to the principal central axis of inertia; J the moment of inertia the link 2. Center of gravity is at the point C (variants 1-4, 6-8,11-13, 16, 18-20, 22-30), or at point A (variants 5, 9, 10, 14, 15, 17, 21). Requires: 1. Calculate the value of control forces and moments at the beginning of the braking of the link 1. Assume that the link 1 starts braking at a time when the angula: acceleration of the link becomes zero. 2. Construct the graphs of control moments and forces as a functions of time. ariant 2 2 m m J J kg x M kg 4T y B 0 2, 2 1,M 0,3 91 T, sec Ct 0,25 K AB=AD=21 p(0) (T) rad T DN T/3