Many small restaurants in Portland, Oregon, and other cities across the United States do not take reservations. Owners say that with smaller capacity, noshows are costly, and they would rather have their staff focused on customer service rather than maintaining a reservation system (pressherald.com). However, it is important to be able to give reasonable estimates of waiting time when customers arrive and put their name on the waiting list. The fileRestaurantLinecontains10observations of number of people in line ahead of a customer (independent variablex) and actual waiting time (dependent variabley). The estimated regression equation is:y = 8.45 + 7.58x andMSE = 121.3989.

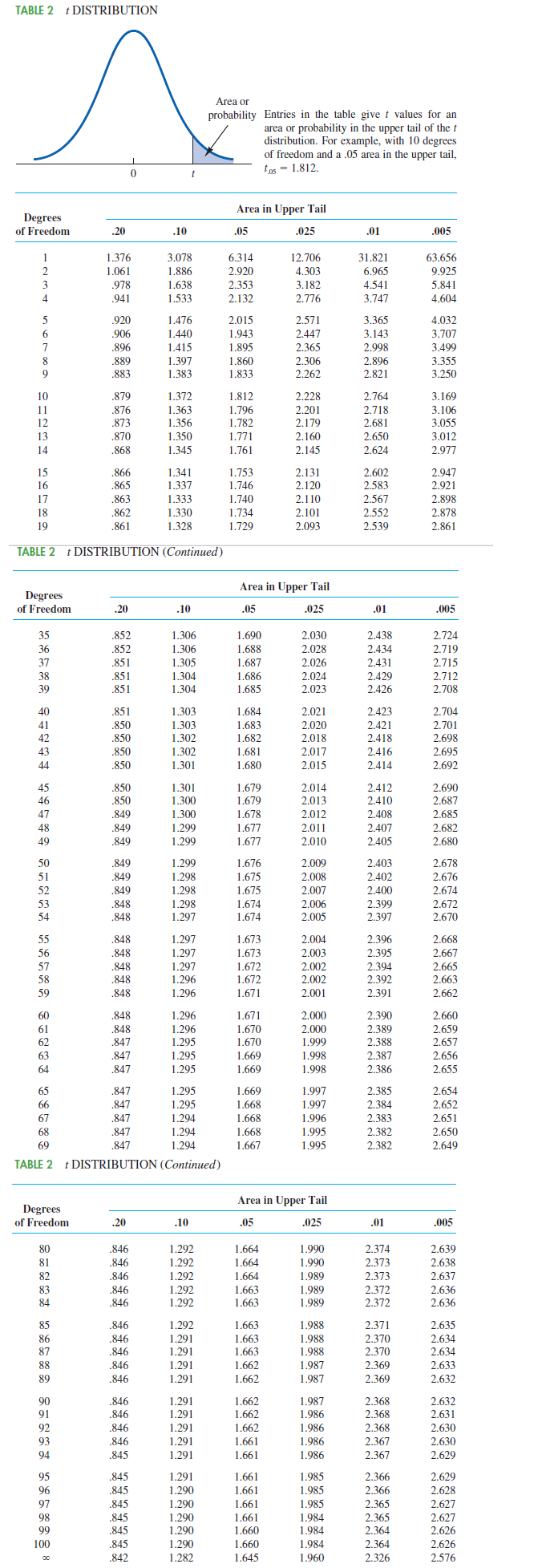
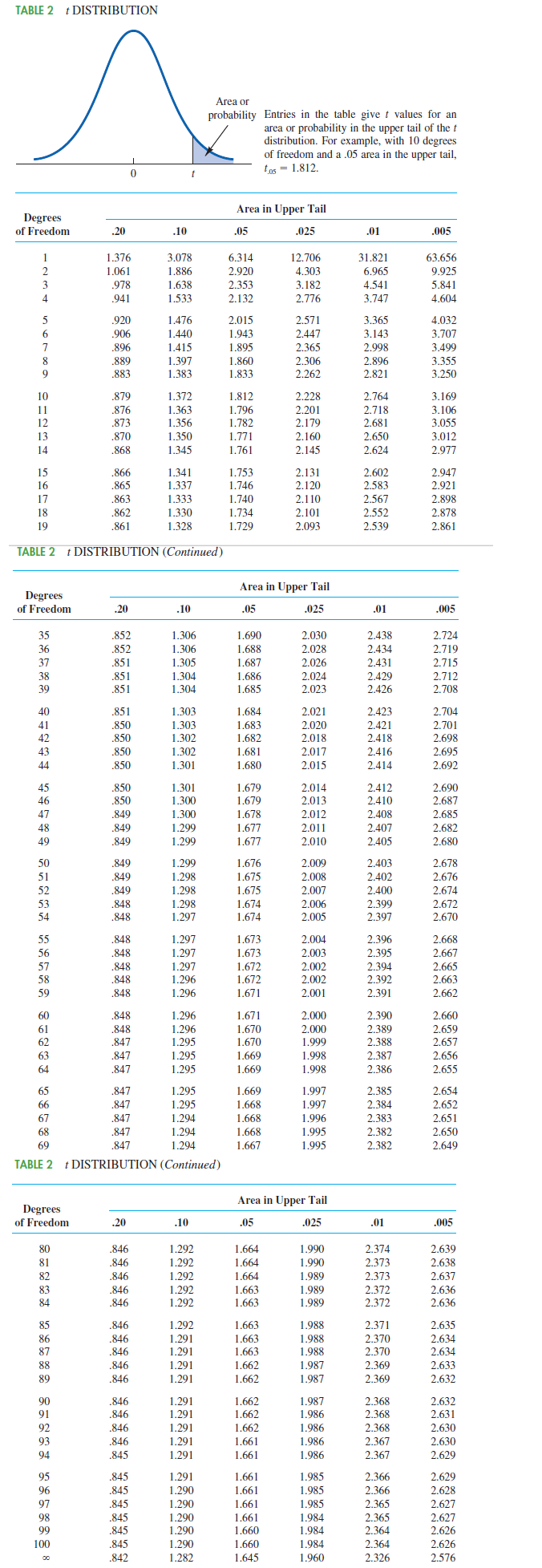
Please see attached table below.

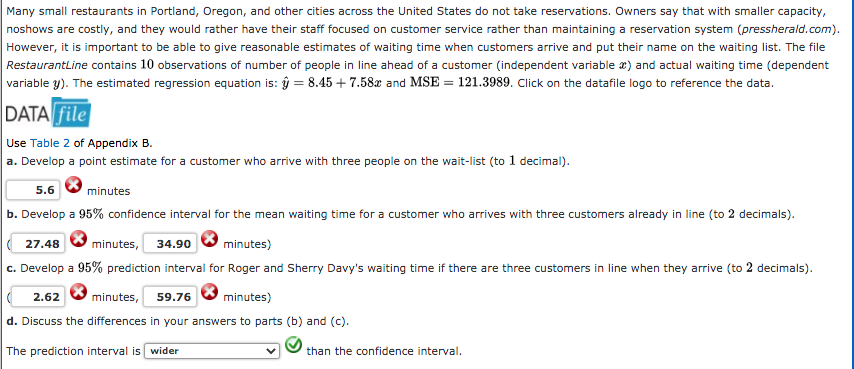
Many small restaurants in Portland, Oregon, and other cities across the United States do not take reservations. Owners say that with smaller capacity, noshows are costly, and they would rather have their staff focused on customer service rather than maintaining a reservation system (pressherald.com). However, it is important to be able to give reasonable estimates of waiting time when customers arrive and put their name on the waiting list. The file RestaurantLine contains 10 observations of number of people in line ahead of a customer (independent variable @) and actual waiting time (dependent variable y). The estimated regression equation is: y = 8.45 + 7.58x and MSE = 121.3989. Click on the datafile logo to reference the data. DATA file Use Table 2 of Appendix B. a. Develop a point estimate for a customer who arrive with three people on the wait-list (to 1 decimal). 5.6 minutes b. Develop a 95% confidence interval for the mean waiting time for a customer who arrives with three customers already in line (to 2 decimals). 27.48 minutes, 34.90 minutes) c. Develop a 95% prediction interval for Roger and Sherry Davy's waiting time if there are three customers in line when they arrive (to 2 decimals). 2.62 minutes, 59.76 minutes) d. Discuss the differences in your answers to parts (b) and (c). The prediction interval is wider than the confidence interval.TABLE 2 DISTRIBUTION Area or probability Entries in the table give t values for an area or probability in the upper tail of the t distribution. For example, with 10 degrees of freedom and a .05 area in the upper tail, 0 tos = 1.812. Area in Upper Tail Degrees of Freedom .20 .10 .0 .025 .01 .005 1.376 3.078 6.314 12.706 31.821 63.656 1.061 1.886 2.920 4.303 6.965 9.925 .978 1.638 2.353 3.182 4.541 5.841 .941 1.533 2.132 2.776 3.747 4.604 DOYOU AWN- 920 1.476 2.015 2.571 3.365 4.032 .906 1.440 1.943 2.447 3.143 3.707 .896 1.415 1.89 2.36 2.998 3.49 .889 1.397 1.860 2.306 2.896 3.355 .883 1.383 1.833 2.262 2.821 3.250 10 .879 1.372 1.812 2.228 2.764 3.169 11 .876 1.363 1.796 2.201 2.718 3.106 .873 1.356 1.782 2.179 2.681 3.05 .870 1.350 1.771 2.160 2.650 3.012 14 .868 1.345 1.761 2.145 2.624 2.977 15 .866 1.341 1.753 2.131 2.602 2.947 16 .865 1.337 1.746 2.120 2.583 2.921 17 .863 1.333 1.740 2.110 2.567 2.898 18 .862 1.330 1.734 2.101 2.552 2.878 10 861 1.328 1.729 2.093 2.539 2.861 TABLE 2 DISTRIBUTION (Continued) Area in Upper Tail Degrees of Freedom .20 .10 05 .025 .01 005 35 .852 1.306 1.690 2.030 2.438 2.724 36 .852 1.306 1.688 2.028 2.434 2.719 37 .851 1.305 1.687 2.026 2.431 2.715 38 .851 1.304 1.686 2.024 2.429 2.712 30 .851 1.304 1.685 2.023 2.426 2.708 40 .851 1.303 1.684 2.021 2.423 2.704 41 .850 1.303 1.683 2.020 2.421 2.701 42 .850 1.302 1.682 2.018 2.418 2.698 43 .850 1.302 1.681 2.017 2.416 2.695 44 .850 1.301 1.680 2.015 2.414 2.692 .850 1.301 1.679 2014 2.412 2.690 .850 1.300 1.679 2.013 2.410 2.687 .849 1.300 1.678 2.012 2.408 2.685 .849 1.299 1.677 2.011 2.407 2.682 .849 1.299 1.677 2.010 2.405 2.680 .849 1.299 1.676 2.009 2.403 2.678 .849 1.298 1.675 2.00 2.402 .849 1.298 1.675 2.007 2.400 2.674 .848 1.298 1.674 2.006 2.399 2.672 .848 1.297 1.674 2.005 2.397 2.670 .848 1.297 1.673 2.004 2.396 2.668 .848 1.297 1.673 2.003 2.395 2.667 .848 1.297 1.672 2.002 2.394 2.665 .848 1.296 1.672 2.00 2.392 2.663 .848 1.296 1.671 2.001 2.391 2.662 .848 1.296 1.671 2.000 2.390 2.660 .848 1.296 1.670 000 C 2.389 2.659 .847 1.295 1.670 1 999 2.388 2.657 .847 1.295 1.669 1.998 2.387 2.656 .847 1.295 1.669 1.998 2.386 2.655 .847 1.295 1.669 1.997 2.385 2.654 .847 1.295 1.668 1.997 2.384 2.652 .847 1.294 1.668 1.996 2.383 2.651 .847 1.294 1.668 1.995 2.382 2.650 .847 1.294 1.667 1.995 2.382 2.649 TABLE 2 DISTRIBUTION (Continued) Area in Upper Tail Degrees of Freedom .20 .10 05 .025 .01 .005 .846 1.292 1.664 1.990 2.374 2.639 .846 1.292 1.664 1.990 2.373 2.638 .846 1.292 1.664 1.989 2.373 2.637 83 .846 1.292 1.663 1.989 2.372 2.636 84 .846 1.292 1.663 1.989 2.372 2.636 85 846 1.292 1.663 1.988 2.371 2.635 86 .846 1.291 1.663 1.988 2.370 2.634 87 .846 1.291 1.663 1.988 2.370 2.634 88 .846 1.291 1.662 1 987 2.369 2.633 89 .846 1.291 1.662 1.987 2.369 2.632 90 .846 1.291 1.662 1.987 2.368 2.632 91 .846 1.291 1.662 1.986 2.368 2.631 92 .846 1.291 1.662 1.986 2.368 2.630 93 .846 1.291 1.66 1.986 2.367 2.630 94 .845 1.291 1.661 1.986 2.367 2.629 95 .845 1.291 1.661 1.985 2.366 2.629 96 .845 1.290 1.661 1.985 2.366 2.628 97 845 1.290 1.661 1 985 2.365 2.627 98 .845 1.290 1.661 1.984 2.365 2.627 99 845 1.290 1.660 1.984 2.364 2.626 100 .845 1.290 1.660 1.984 2.36 2.626 842 1.282 1.645 1.960 2.326 2.576