Math 10 Practice Exam 4

PLS SHOW WORK and ANSWER ALL THE QUESTIONS ---- NO EXCEPTION) (NOTE: your answer should be among the multiple choice questions/ answer if it's it means your is wrong so pls do your correctly and carefully!!!!!) NO MADE UP ANSWERS PLS AND THANK YOU!!!!!)

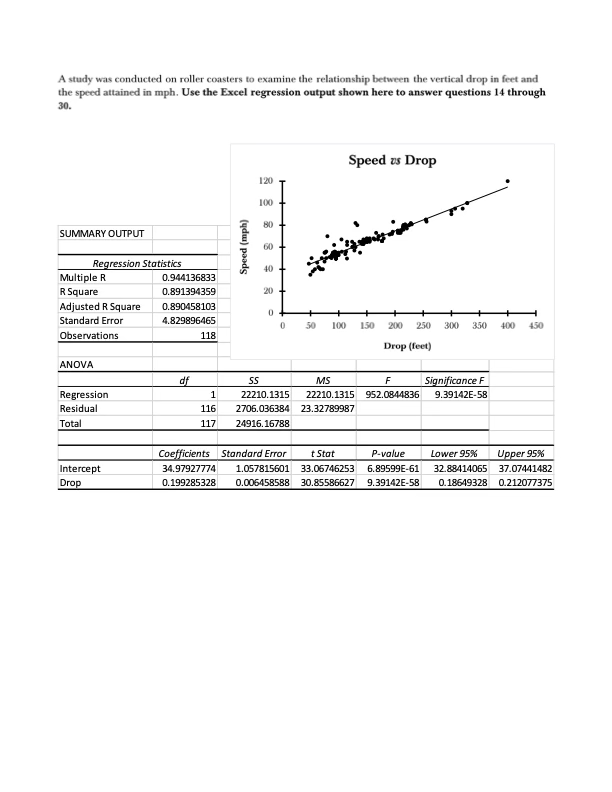
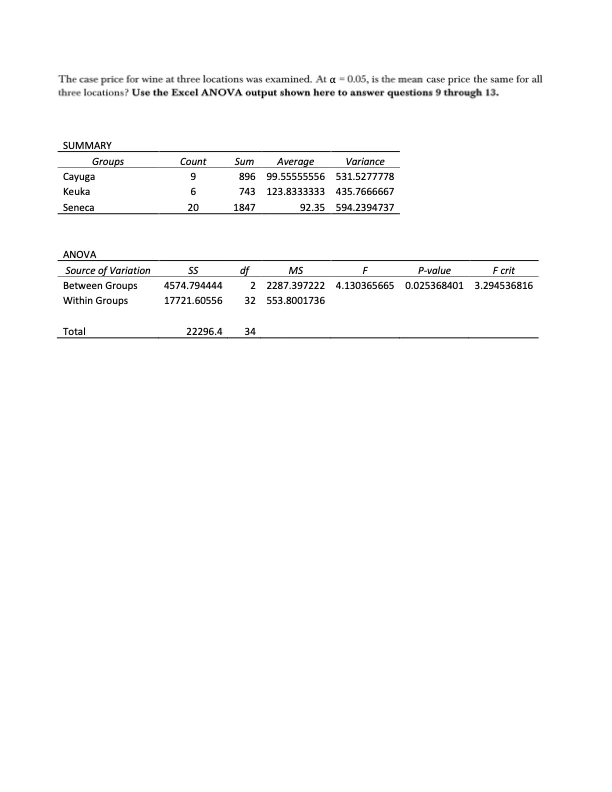
For Questions 9 - 30, use the pdf file Practice Exam 4 - ANOVA and Regression Excel output locatedin the Discussions section.

Question 1

A researcher wonders whether an association exists between car color and the likelihood of being in an accident. Sample data were gathered and are shown below. Calculate the test statistic value for testing whether car color is independent of accident likelihood.

?	Red	Black	White
Car has been in an accident	26	21	30
Car has not been in an accident	27	35	41

A.) 1.50

B.) 1.92

C.) 1.83

D.) 1.71

E.) 1.64

Question 2

A medical study examined the average effect of a new treatment regimen and obtained the following summary statistics.

Treatment	Control
x1 = 101.4	x2 = 99.7
s1 = 1.4	s2 = 1.3
n1 = 8	n2 = 6

Can it be concluded that the average effect for the treatment regimen is greater than for the control? Estimate the P-value for a test of this claim.

A.) 0.02 P-value

B.) 0.01 P-value

C.) 0.025 P-value

D.) 0.05 P-value

E.) 0.10 P-value

Question 3

According to the manufacturer of M&M candy, the color distribution for plain chocolate M&Ms is 13% brown, 13% red, 14% yellow, 24% blue, 20% orange, and 16% green. A 1.69-ounce bag of plain chocolate M&Ms was opened, and the counts for each of the colors noted. The results are shown below. Are the sample data consistent with the manufacturer's claim? Compute the test statistic value for a test of the claim.

Color	Brown	Red	Yellow	Blue	Orange	Green
Observed	10	4	5	15	12	10

A.) 3.301

B.) 3.724

C.) 3.882

D.) 3.675

E.) 3.533

Question 4

A farmer decided to use a new additive to grow his crops. He divided his farm into 10 plots and kept records of the corn yield (in bushels) before and after using the additive. The results are shown below. Do the data support the conclusion that the additive increases plot yield? Compute the test statistic value for a test of the claim.

Before	9	9	8	7	6	10	5	9	10	11
After	10	9	9	8	7	8	6	10	9	12

A.) -1.177

B.) -2.306

C.) -1.584

D.) -0.400

E.) -2.551

Question 5

In a study of mean body temperatures for men and women, the following table was obtained.

Men	Women
x1= 98.105	x2= 98.394
= 0.489	= 0.552
n1= 65	n2= 65

Construct a 90% confidence interval for?₁-?₂, the difference between the mean body temperature of men and the mean body temperature of women.

A.) -0.537?₁-?₂

B.) -0.440 ?₁-?₂

C.) -0.468 ?₁-?₂

D.) -0.616 ?₁-?₂

E.) -0.498 ?₁-?₂

Question 6

In a sample of 150 men, 132 said that they had less leisure time today than they had 10 years ago. In a random sample of250women, 234 women said that they hadless leisure time than they had 10 years ago. Compute the test statistic value for a test of whether the proportions are the same or not.

A.) -1.94

B.) -1.82

C.) -1.57

D.) -1.68

E.) -1.76

Question 7

According to Benford's Law, a variety of data sets include numbers with leading (first) digits that obey the following distribution: 30.1% are 1, 17.6% are 2, 12.5% are 3, 9.7% are 4, 7.9% are 5, 6.7% are 6, 5.8% are 7, 5.1% are 8, and 4.6% are 9. When working with the district attorney, a fraud investigator analyzed the leading digits of the amounts from 784 checks issued by a suspect company. The observed data are shown below. If the observed frequencies are substantially different from the frequencies expected from Benford's Law, the check amounts appear to result from fraud.

Digit	1	2	3	4	5	6	7	8	9
Observed	251	114	86	67	89	52	47	42	36

Suppose the test statistic value is ?² = 19.655 for a chi-square goodness-of-fit test comparing the observed data with Benford's Law. Using ? = 0.01, is there sufficient evidence to conclude the checks are the result of fraud?

A.) H₀ is not rejected. The checks are not the result of fraud.

B.) H₀ is rejected. The checks are the result of fraud.

C.) H₀ is rejected. The checks are not the result of fraud.

D.) H₀ is not rejected. The checks are the result of fraud.

Question 8

A study was conducted on the percentages of on-time arrivals for major U.S. airlines. Two regional airlines were surveyed. For Airline A, 213 out of 300 flights were on-time. For Airline B, 185 out of 250 were on-time. Construct a 90% confidence interval for the difference between the proportions of flights that are on-time for Airline A and Airline B.

A.) -0.093 p₁ - p₂

B.) -0.128 p₁ - p₂

C.) -0.079 p₁ - p₂

D.) -0.119 p₁ - p₂

E.) -0.105 p₁ - p₂

Question 9

What is the ANOVA F test statistic value?

A.) 0.0254

B.) 4.130

C.) 3.295

D.) 32

E.) 34

Question 10

What is the critical value for the test?

A.) 34

B.) 32

C.) 0.0254

D.) 3.295

E.) 4.130

Question 11

What is the P-value for the test?

A.) 34

B.) 3.295

C.) 0.0254

D.) 4.130

E.) 32

Question 12

Is the null hypothesis rejected?

A.) No

B.) Yes

Question 14

Which phrase best describes the relationship between the two variables?

A.) positive linear relationship

B.) negative linear relationship

C.) no discernable relationship

D.) nonlinear (curvilinear) relationship

Question 15

What is the value of the coefficient of determination?

A.) 0.944

B.) 0.199

C.) 0.972

D.) 0.891

E.) 4.830

Question 16

What is the value of the sample correlation coefficient?

A.) 0.972

B.) 0.199

C.) 0.891

D.) 4.830

E.) 0.944

Question 17

What is the sample size?

A.) 118

B.) 116

C.) 120

D.) 119

E.) 117

Question 18

What is the explanatory variable?

A.) drop

B.) speed

Question 19

What is the response variable?

A.) speed

B.) drop

Question 20

What is the test statistic value for the hypothesis test concerning the existence of a linear relationship between the two variables?

A.) 34.979

B.) 0.199

C.) 33.067

D.) 4.830

E.) 30.856

Question 21

What is the P-value for the hypothesis test concerning the existence of a linear relationship between the two variables?

A.) 0.05 P-value

B.) 0.01 P-value

C.) P-value

D.) P-value > 0.10

Question 22

What is the conclusion for the hypothesis test concerning the existence of a linear relationship between the two variables?

A.) A nonlinear (curvilinear) relationship exits.

B.) Cannot be determined.

C.) A linear relationship exists.

D.) No linear relationship exists.

Question 23

What percentage of the variation in the observed speeds is explained by a linear relationship between drop and speed?

A.) 89.1%

B.) 4.83%

C.) 97.2%

D.) 95.0%

E.) 94.4%

Question 24

What is the linear regression equation?

A.) y' = 34.979 + 1.058x

B.) y' = 34.979 + 0.199x

C.) y' = 0.199 + 0.006x

D.) y' = 0.199 + 34.979x

Question 25

What is the estimated standard deviation for the residuals (i.e., s_est ) ?

A.) 34.979

B.) 4.830

C.) 1.058

D.) 0.006

E.) 0.199

Question 26

What speed does the linear regression model predict for a drop of 144 feet?

A.) 61.7 mph

B.) 65.1 mph

C.) 71.3 mph

D.) 63.6 mph

E.) 69.8 mph

Question 27

What is the residual that corresponds to the observed data point (144, 67)?

A.) -3.4

B.) 2.8

C.) -2.8

D.) 3.4

E.) 1.9

Question 28

What is the 95% confidence interval for the slope of the regression line?

A.) (32.884, 37.074)

B.) (30.856, 33.067)

C.) (0.186, 0.212)

D.) (0.006, 1.058)

Question 29

What is the meaning of the slope estimate b = 0.199 as it relates drop to speed?

A.) For every increase of 199 feet in drop, speed increases by 100 mph.

B.) For every increase of 19.9 feet in drop, speed increases by 1 mph.

C.) For every increase of 100 feet in drop, speed increases by 1.99 mph.

D.) For every increase of 10 feet in drop, speed increases by 19.9 mph.

E.) For every increase of 100 feet in drop, speed increases by 19.9 mph.

Question 30

What does the linear regression model predict would be the change in speed given an increase in drop of 80 feet?

A.) about 48 mph faster

B.) about 8 mph faster

C.) about 16 mph faster

D.) about 32 mph faster

E.) about 64 mph faster

A study was conducted on roller coasters to examine the relationship between the vertical drop in feet and the speed attained in mph. Use the Excel regression output shown here to answer questions 14 through 30. Speed as Drop 120 100 SUMMARY OUTPUT Speed (mph) Regression Statistics 40 Multiple R 0.944136833 R Square 0.891394359 Adjusted R Square 0.890458103 Standard Error 4.829896465 50 100 150 200 250 300 350 400 450 Observations 118 Drop (feet) ANOVA of 55 MS F Significance F Regression 1 22210.1315 22210.1315 952.0844836 9.39142E-58 Residual 116 2706.036384 23.32789987 Total 117 24916.167 Coefficients Standard Error Stot P-value Lower 95%% Upper 95% Intercept 34.97927774 1.057815601 33.06746253 6.89599E-61 32. 88414065 37.07441482 Drop 0.199285328 0.006458588 30.85586627 9.39142E-58 0.18649328 0.212077375The case price for wine at three locations was examined. At a = 0.05, is the mean case price the same for all three locations? Use the Excel ANOVA output shown here to answer questions 9 through 13. SUMMARY Groups Count Sum Average Variance Cayuga 9 896 99.55555556 531.5277778 Keuka 6 743 123.8333333 435.7666667 Seneca 20 1847 92.35 594.2394737 ANOVA Source of Variation of M F P-value F crit Between Groups 4574.794444 2 2287.397222 4.130365665 0.025368401 3.294536816 Within Groups 17721.60556 32 553.8001736 Total 22296.4 34