
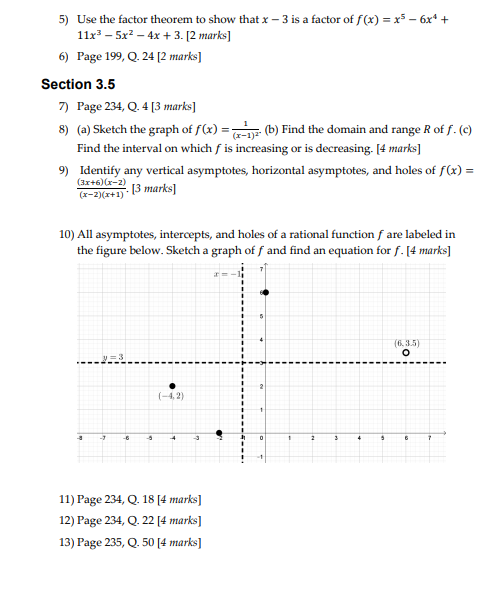
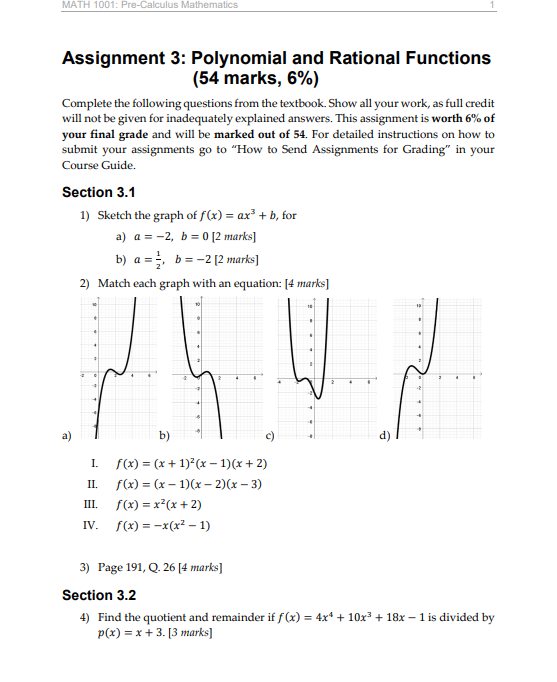

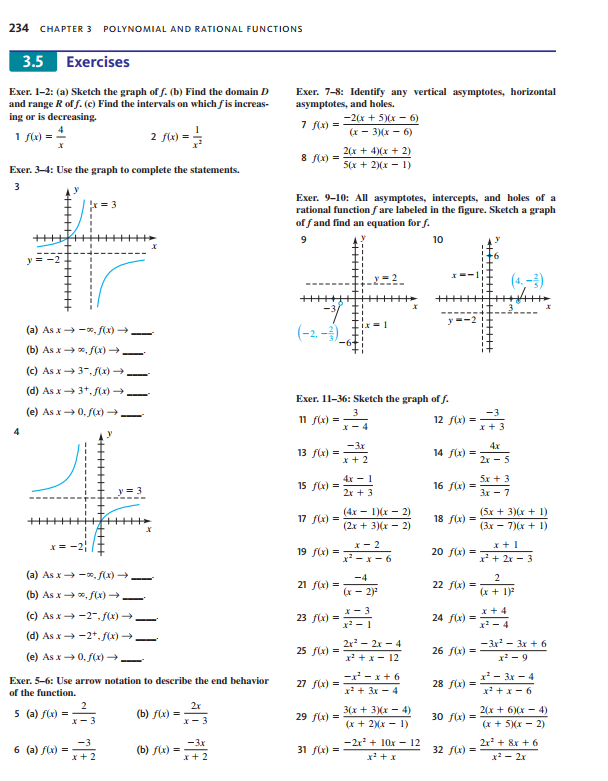


MATH 1001: Pre-Calculus Mathematics 3 14) Find an equation of a rational function f that satisfies the given conditions: |4 marks] Vertical asymptotes: x = -5,x = 2 Horizontal asymptotes: y = -2 x-intercepts: x = -6,x = 4 f(-2) = -4 Section 3.6 15) Page 241, Q. 10 [2 marks] 16) Page 241, Q. 34 [3 marks]5) Use the factor theorem to show that x - 3 is a factor of / (x) = x5 - 6x* + 11x3 - 5x2 - 4x + 3. [2 marks] 6) Page 199, Q. 24 [2 marks] Section 3.5 7) Page 234, Q. 4 [3 marks] 8) (a) Sketch the graph of f(x) = 7_TE (b) Find the domain and range R of f. (c) Find the interval on which f is increasing or is decreasing. [4 marks] 9) Identify any vertical asymptotes, horizontal asymptotes, and holes of f(x) = (3r+6) (x-2) (x-2](r+1) . [5 marks] 10) All asymptotes, intercepts, and holes of a rational function f are labeled in the figure below. Sketch a graph of f and find an equation for f. [4 marks] (6. 3.5) O 2 (-4,2) 11) Page 234, Q. 18 [4 marks] 12) Page 234, Q. 22 [4 marks] 13) Page 235, Q. 50 [4 marks]MATH 1001: Pre-Calculus Mathematics Assignment 3: Polynomial and Rational Functions (54 marks, 6%) Complete the following questions from the textbook. Show all your work, as full credit will not be given for inadequately explained answers. This assignment is worth 6% of your final grade and will be marked out of 54. For detailed instructions on how to submit your assignments go to "How to Send Assignments for Grading" in your Course Guide. Section 3.1 1) Sketch the graph of f(x) = ax + b, for a) a = -2, b = 0 [2 marks] b) a= =, b= -2 [2 marks] 2) Match each graph with an equation: [4 marks] a) b) c) d) I. f(x) = (x+ 1)(x - 1)(x +2) II. f(x) = (x - 1)(x - 2)(x - 3) III. f(x) = x3(x+2) IV. f(x) = -x(x -1) 3) Page 191, Q. 26 [4 marks] Section 3.2 4) Find the quotient and remainder if f(x) = 4x* + 10x3 + 18x - 1 is divided by p(x) = x + 3. [3 marks]3.6 Variation 241 W = 125 Wid- Guideline 4 To answer the question, we substitute w = 2, d = 8, and / = 10 into the formula found in guideline 3, obtaining W = 125 . 2 . 8' 10 - = 1600 lb. 3.6 Exercises Exer. 1-16: Express the statement as a formula that involves 12 r is directly proportional to the product of s and v and the given variables and a constant of proportion- inversely proportional to the cube of p. If s = 2, v = 3, and ality k, and then determine the value of & from the given p = 5, then r = 40. conditions. r - kik - 250 1 a is directly proportional to v. If v = 30, then a = 12. 13 q is inversely proportional to the sum of x and y. If x = 0.5 and y = 0.7, then q = 1.4. 2 s varies directly as f. If r = 10, then s = 18. s - kr, x - ! * : x - 1.68 14 y is directly proportional to x and inversely proportional to 3 V varies directly as the cube of r. If r = 3, then V = 36r. the sum of rand s. If x = 3, F = 5, and s = 7, then y = 2. Y - K . K - S 4 8 is directly proportional to the square of x. If x = 2, then 15 y is directly proportional to the square root of x and $ = 24. 5 - Wr k - 6 inversely proportional to the cube of z. If x = 9 and z = 2, then y = 5. 5 p varies directly as s and inversely as t. If s = -2 and t = 4, then r = 7. 16 y is directly proportional to the square of x and inversely r - k=;k- -14 proportional to the square root of z. If x = 5 and z = 16, then y = 10. 6 w varies directly as z and inversely as the square root of a. If z = 2 and u = 9, then w = 6. W-;x-9 17 Liquid pressure The pressure P acting at a point in a liquid is directly proportional to the distance d from the sur- 7 y is directly proportional to the square of x and inversely proportional to the cube of z. If x = 5 and z = 3, then face of the liquid to the point. y = 25. (a) Express P as a function of d by means of a formula that y- KJ; k - 27 involves a constant of proportionality &. P - kd 8 y is directly proportional to x and inversely proportional to (b) In a certain oil tank, the pressure at a depth of 2 feet is the square of z. If x = 4 and z = 3, then y = 16. 1 18 1b/fr. Find the value of & in part (a). y- kj:x- 36 (c) Find the pressure at a depth of 5 feet for the oil tank 9 z is directly proportional to the product of the square of x in part (b). 295 Thyn] and the cube of y. If x = 7 and y = -2, then z = 16. z - krlyh k - - 7 (d) Sketch a graph of the relationship between P and d for 10 z is directly proportional to the product of x and the cube root of y. If x = 2 and y = 8, then z = 12. 18 Hooke's law Hooke's law states that the force F required to stretch a spring & units beyond its natural length is directly proportional to x. 11 z is directly proportional to the product of x and y and inversely proportional to the cube root of w. If x = 6, y = 4, (a) Express F as a function of x by means of a formula that and w = 27, then z = 16. involves a constant of proportionality &. F - kx VW234 CHAPTER 3 POLYNOMIAL AND RATIONAL FUNCTIONS 3.5 Exercises Exer. 1-2: (a) Sketch the graph of f. (b) Find the domain D Exer. 7-8: Identify any vertical asymptotes, horizontal and range R of f. (c) Find the intervals on which fis increase asymptotes, and holes. ing or is decreasing. 7 f(x) = - -2(x + 5)(x - 6) 1 f(x) = 4 2 f(x) = = (x - 3)(x - 6) 8 /(x) = = 2(x + 4)(x + 2) Exer. 3-4: Use the graph to complete the statements. "5(x + )(x - 1) 3 = 3 Exer. 9-10: All asymptotes, intercepts, and holes of a rational function fare labeled in the figure. Sketch a graph of f and find an equation for f. 9 10 -7 (4. - 2) (a) Asx - -x, f(x) (-2, -3) (b) As x - *, f() - (c) As x - 3-,/(x) = (d) As x - 3+, f(x) = Exer. 11-36: Sketch the graph of f. (e) As x - 0,/() = _ 11 /(x) = x - 4 12 /(x) = -3 * + 3 13 f(x) = - -Ar A.x x + 2 14 /(x) = = 2r - 5 = 3 15 f(x) = Ax - 1 2x + 3 16 /C) = 5.x + 3 Ar - 7 17 f(x) = (4x - 1)(x - 2) 18 /(x) = (5x + 3)(x + 1) (2r + 3)(x - 2) (3x - 7) (x + 1) * = x-2 19 /(x) = 1 - x - 6 20 (x) = 1+ 2x - 3 (a) As x - -*, f(x) 21 /(x) = -4 22 (x) = 2 (b) As x - x, /() _ (x - 2)3 (x + 1) (c) As x - -2-, f(x) - 23 /(x) = 12 - 1 24 /(x) =_ I - 4 (d) As x - -2+, f(x) - 25 /(x) = : 2x3 - 2r - 4 -3r - Ir + 6 (e) As x - 0,/() __ x' t x - 12 26 /(x) = - 1 - 9 Exer. 5-6: Use arrow notation to describe the end behavior 27 /(x) = - -F-x+6 28 Mixed - 3x - 4 of the function. x3 + 3x -4 x3+x-6 5 (a) f(x) = 2r x - 3 (b) fix) = Y - 3 29 /() = 24 3(x + 3)(x - 4) 30 fix) = 4(x + 6)(x - 4) (x + 2)(x - 1) (r + 5)(x - 2) 6 (a) f(x) = (b) fix) = -3x 31 /(x) = _2r + 10x - 12 2 + & + 6 x + 2 x + 2 32 /(x) = x3 - 2x3.2 Properties of Division 199 The easiest way to find the remainder using a graphing utility is to simply find the function value Y, when x = -1.37. However, the purpose of this example was to point out the graphical relationship to the division process. 3.2 Exercises Exer. 1-8: Find the quotient and remainder iff(x) is divided 22 degree 3; zeros -3, 0, 4 by p(x). 1 f(x) = 2x* - x' - 3x' + 7x - 12; p(x) = x] - 3 23 degree 4: zeros -2,$1, 4 24 degree 4; zeros -3, 0, 1, 5 2 f(x) = 3r*+ 2x-x-x-6; p(x) =x+ 1 3 /(x) = 3r' + 2x - 4; p(x) = 283 + 1 Exer. 25-32: Use synthetic division to find the quotient and remainder if the first polynomial is divided by the second. 4 f(x) = 1 - 5p - 4x - 8; p(x) = 2x3 + x 25 2r' - 3x3 + 4x - 5; x - 2 5 /(x) = 7x + 2; p(x) = 2x - x - 4 26 Ar' + 10x3 - 7x + 8 x + 4 6 f(x) = -5x3 + 3; p(x) = x- 3x+ 9 27 x - &r - 5; r+3 28 5x - 18x3 - 15; 7 /(x) = 10x + 4; p(x) = 2x - 5 29 Ar' + 6r' + 7; 8 f(x) = 70'+ 3x - 10; p(x)=x - x+ 10 30 -2x* + 10x - 3; x - 3 Exer. 9-12: Use the remainder theorem to find fle). 31 4r - 5r' + 1; 9 f(x) = 3-x -4; c = 2 32 9r' - 6r' + 3x - 4; x- 10 f(x) = 2r' + 4x' - 3x - 1; c = 3 11 f(x) = x - 6r' + 4x - 8; c= -3 Exer. 33-40: Use synthetic division to find fic). 12 fix) = x4 + 3 - 12; c= -2 33 /(x) = 2r' + 3x - Ar + 4; c= 3 Exer. 13-18: Use the factor theorem to show that r - c is a 34 /(x) = -x+ 4x+ x C= -2 factor of f(x). 35 /(x) = 0.3x3 + 0.4r; c=-0.2 13 /(x) = x + x - 2r + 12; c= -3 36 /(x) = 0. Lr' + 0.5x C = 0.3 14 /x) =r ty' - Ilx+ 10; c = 2 37 /(x) = 27r + 2p' + 1 c= : 15 /(x) = 1" - 4096; c= -2 38 /(x) = &r' - 3x3 + 7; 16 /(x) = > + 1024; C= -4 39 /(x) = x' + 3 - 5; c = 2+ V3 17 f(x) = x - 2p' + 3x - 36; c= ] 18 fix) = x - 3 + 5x - 2, c= 2 40 fix) = x - 1 - 8; c= 1+ v2 Exer. 19-24: Find a polynomial f(x) with leading coefficient Exer. 41-44: Use synthetic division to show that e is a zero I and having the given degree and zeros. of fur). 19 degree 3; zeros -2, 0, 5 41 (x) = 3 + & - 2p3 - 10r + 4; c= -2 20 degree 3; zeros 12, 3 42 f(x) = 4x3 - 9x3 - &x - 3; c = 3 21 degree 3; zeros 13, I 43 f(x) = 4' - 6r' + 8 - 3;3.1 Polynomial Functions of Degree Greater Than 2 191 (c) (d) 29 /(x) = (x + 2)(x - 1)3(x - 2) 30 /(x) = x(x + 1)'(x - 2)(x - 4) Exer. 31-32: Sketch the graph of a polynomial given the 7 1 sign diagram. 31 Sign of f(x) (A) f(x) = x(x - 1) (B) f(x) = -xx + 2) 3.2 (C) f(x) = (x + 2)(x+ 1)(x - 3) Sign of f(x) + (D) (x) = (x + 2)(x + 1(x - 1) -3 -2 0 Exer. 13-14: Use arrow notation to describe the end behav- 33 (a) Sketch a graph of ior of the function. Do not sketch the graph. f(x) = (x - a)(x - b)(x - c). 13 (a) /(x) = 3x - 2r + 6 where a (? (d) fux) = -2+ 3x -6 (d) What is the solution to /(x) = (? 35 Let f(x) be a polynomial such that the coefficient of every Exer. 15-30: Find all values of r such that f(x) > 0 and all r odd power of x is 0. Show that f is an even function. such that f(r) 0 and all x such that P(x)




















