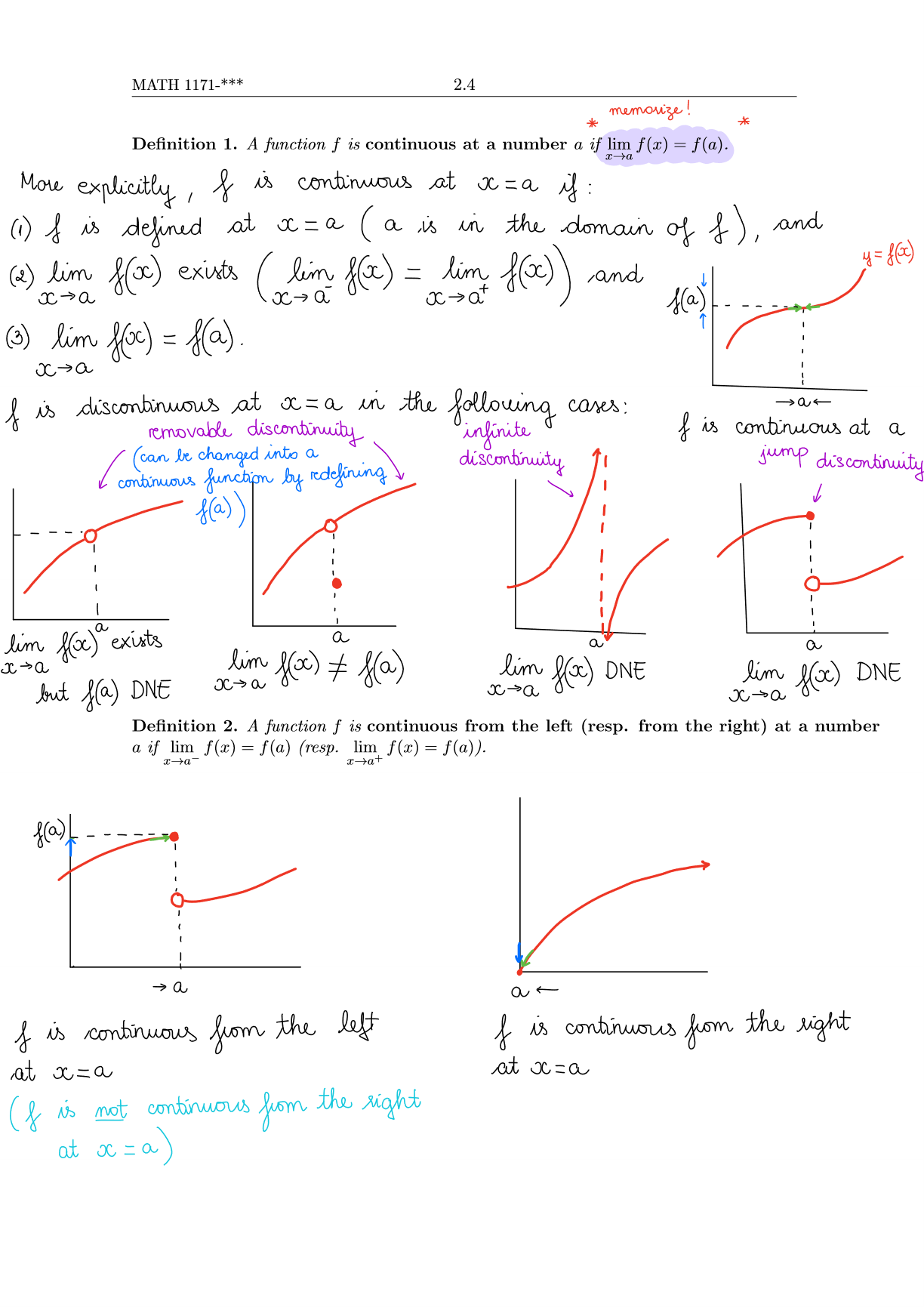
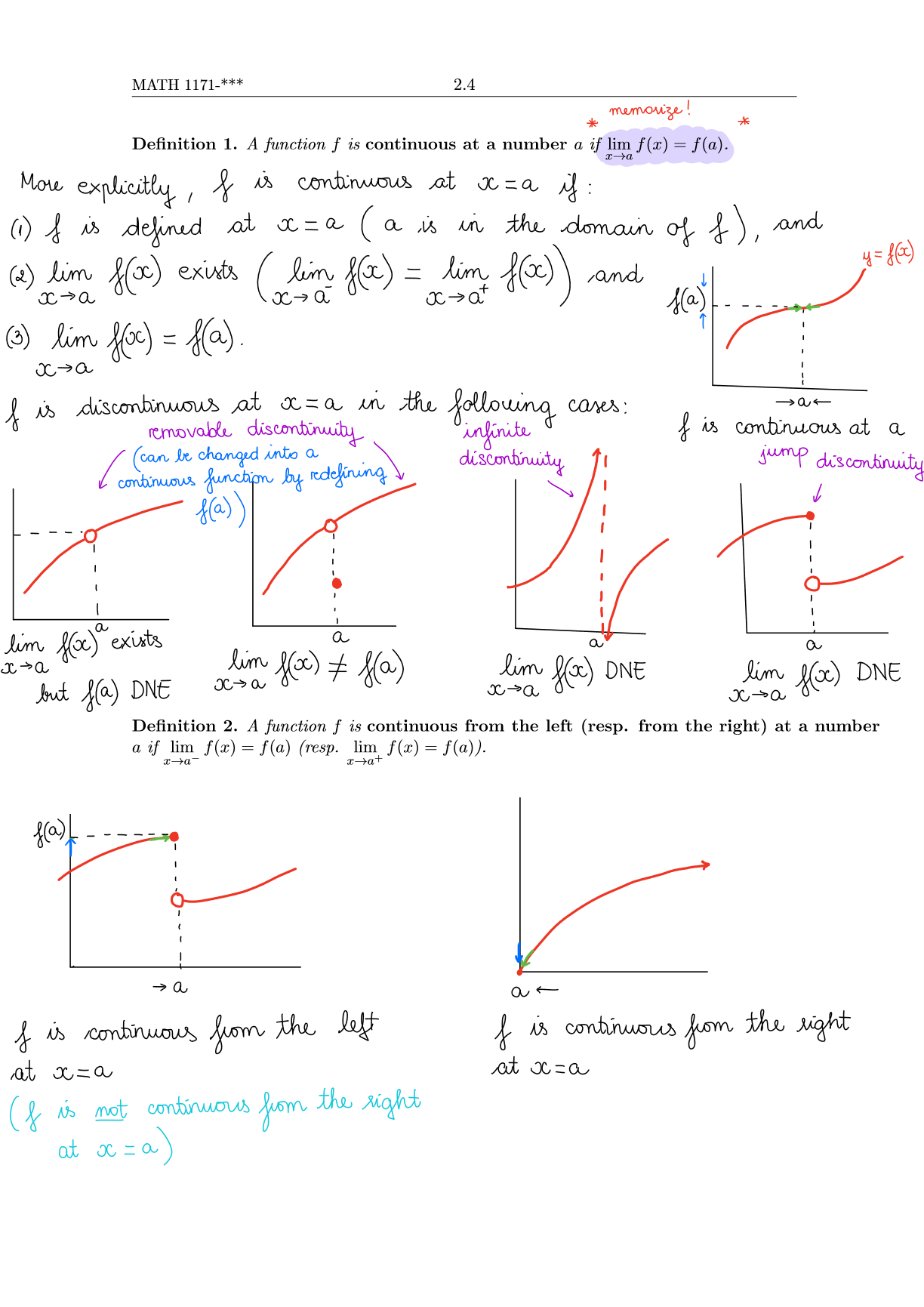
MATH 1171-*** 2.4 memorize! Definition 1. A function f is continuous at a number a if lim (x) = f(a). More explicitly, I is continuous at x=a if (1) I is defined at x = a ( : x a * a is in the domain of f), and (2) lim f(oc) exists ( lim f(x) = lim f(x)) and xa (3) lim f(xx) = f(a). xa x>> a+ f is discontinuous at x = a in the removable discontinuity (can be changed into a continuous function by redefining f(a) following infinite discontinuity cases: y= f(oc) 1a f is continuous at a jump discontinuity a lim f(x) # f(a) a lim f(oc) exists xa but f(a) DNE xc a a lim f(c) DNE xa a lim f(x) DNE xa Definition 2. A function f is continuous from the left (resp. from the right) at a number a if lim f(x) = f(a) (resp. lim f(x) = f(a)). x-a- xa+ f(a) | a I is continuous from the left at x=a (f is not continuous from the right at x = a x = a) a If is continuous from the right at x=a