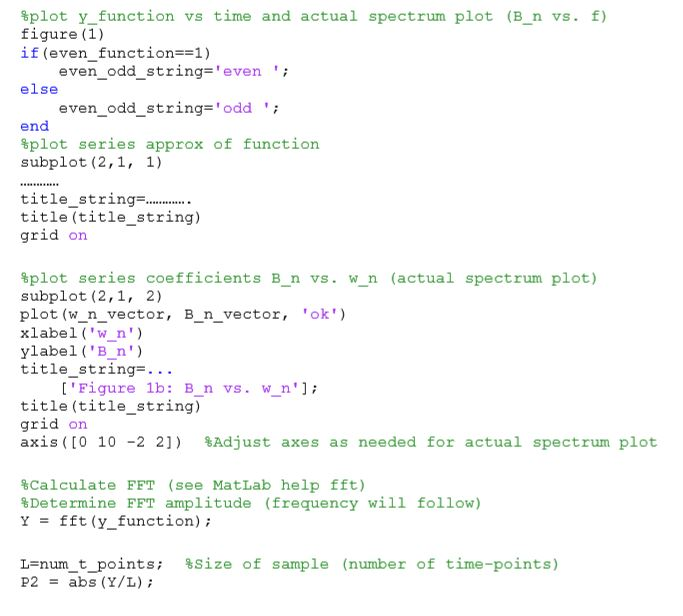
Matlab Component: You are provided with a fragment of a MatLab code which calculates and plots a Fourier series y(t)-B :1 B co (a, t) or y(t) B+ 1B, sin(a) t). The code plots a ramp", "triangle" and "square" periodic function with period T. The code requires inputs such as the number of terms N to sum in the series and the number of periods to plot. In addition, the code can sum an even or odd series as specified. The main code is given below: F urier series c de clear all close all clc %Inputs num-t-points-300 %number of plotting points in t (must be even for fft operation) T-2 %Period of function (seconds) even function-0 %1->even, 0:>odd nterms-200 %number of terms in Fourier series to sum nPeriodsPlot-3% number of periods to plot (will start at -T*((n-1)+.5) - Band end at -T* ((n-1) +.5)),i.e. centered about zero %1=>ramp, %5 > User defined function-type-3 2 triangle (odd), square 3, unit amplitude spike=>4 %create t vector (plot centered max-t=T* (n-periods_plot) /2; min t--T* (n_periods_plot)/2; t-vector=linspace (max-t, mint, around t 0) t-points) ; num Calculate terms in Fourier series [B n vect r, B 0, w n ve ct r]=calc B n vector (n terms , T, functi n type) ; %Calculate f n w n/ (2*pi) for pl tting purposes %Allocate y-function y function-zeros (1, num_t_points): for J-1 : num-t-points y-function (j) =B 0; for k-1:n terms if (even function--1) y-function (j) = y function (j) +B_n vector (k) *cos (w n_vector (k) *t vector (j)) elseif (even function=0) end end end Splot y function vs time and actual spectrum plot (B n vs. f) figure (1) if (even function== 1 ) even odd string'even ' else even odd string 'odd end plot series approx of function subplot (2,1, 1) title_string.. . title (title_string) grid on %plot series coefficients B n vs. w n (actual spectrum plot) subplot (2,1, 2) plot (w n vector, B n vector, ok xlabel'W n' ylabel ('B n') title string. [ 'Figure 1b: B n vs wn'; title (title string) grid on axis([0 10-2 2]) %Adjust axes as needed for actual spectrum plot Calculate FFT (see MatLab help fft) Determine FFT amplitude (frequency will follow) Yfft (y function) 1-num-t-points; P2 = abs (Y/L) ; size of sample (number of time-points) P1P2 (1:L/2+1) P1 (2:end-12*P1 (2:end-1); Fs-num t points/ (T*n_periods_plot) f = Fs * (0: (L/ 2) ) /L; figure (2) plot (f, P1) title ('Figure 2 Single-sided Amplitude Spectrum of y (t) xlabel (Hz)) ylabel'IBnl' grid on axis ([0 10 0 2]) %Adjust axe s as needed for fft plot calculate Nyquist frequency and compare with highest component freq. Note that the function calc_B_n vector is called but not provided. This function uses the function period, function type and number of terms to sum, as inputs. The outputs are the coefficient terms Bo and B" for the series, as well as the corresponding angular velocities . In addition, you must compare the component max frequency with the Nyquist frequency to ensure an accurate spectrum plot using FFT. Deliverables: Write an operable function calc_B_n vector and run your program to produce: a) Ramp (upward sloping saw-tooth) b) Triangle c) Square In addition, your code must print (display) the Nyquist and max frequency component! Finally, note that some parts of the main program are missing and must be re-written! In your code, all three series will sum the first 200 terms, have a fundamental period of two seconds, plot three full periods of the cycle and populate those three periods with a total of 4000 data-points Matlab Component: You are provided with a fragment of a MatLab code which calculates and plots a Fourier series y(t)-B :1 B co (a, t) or y(t) B+ 1B, sin(a) t). The code plots a ramp", "triangle" and "square" periodic function with period T. The code requires inputs such as the number of terms N to sum in the series and the number of periods to plot. In addition, the code can sum an even or odd series as specified. The main code is given below: F urier series c de clear all close all clc %Inputs num-t-points-300 %number of plotting points in t (must be even for fft operation) T-2 %Period of function (seconds) even function-0 %1->even, 0:>odd nterms-200 %number of terms in Fourier series to sum nPeriodsPlot-3% number of periods to plot (will start at -T*((n-1)+.5) - Band end at -T* ((n-1) +.5)),i.e. centered about zero %1=>ramp, %5 > User defined function-type-3 2 triangle (odd), square 3, unit amplitude spike=>4 %create t vector (plot centered max-t=T* (n-periods_plot) /2; min t--T* (n_periods_plot)/2; t-vector=linspace (max-t, mint, around t 0) t-points) ; num Calculate terms in Fourier series [B n vect r, B 0, w n ve ct r]=calc B n vector (n terms , T, functi n type) ; %Calculate f n w n/ (2*pi) for pl tting purposes %Allocate y-function y function-zeros (1, num_t_points): for J-1 : num-t-points y-function (j) =B 0; for k-1:n terms if (even function--1) y-function (j) = y function (j) +B_n vector (k) *cos (w n_vector (k) *t vector (j)) elseif (even function=0) end end end Splot y function vs time and actual spectrum plot (B n vs. f) figure (1) if (even function== 1 ) even odd string'even ' else even odd string 'odd end plot series approx of function subplot (2,1, 1) title_string.. . title (title_string) grid on %plot series coefficients B n vs. w n (actual spectrum plot) subplot (2,1, 2) plot (w n vector, B n vector, ok xlabel'W n' ylabel ('B n') title string. [ 'Figure 1b: B n vs wn'; title (title string) grid on axis([0 10-2 2]) %Adjust axes as needed for actual spectrum plot Calculate FFT (see MatLab help fft) Determine FFT amplitude (frequency will follow) Yfft (y function) 1-num-t-points; P2 = abs (Y/L) ; size of sample (number of time-points) P1P2 (1:L/2+1) P1 (2:end-12*P1 (2:end-1); Fs-num t points/ (T*n_periods_plot) f = Fs * (0: (L/ 2) ) /L; figure (2) plot (f, P1) title ('Figure 2 Single-sided Amplitude Spectrum of y (t) xlabel (Hz)) ylabel'IBnl' grid on axis ([0 10 0 2]) %Adjust axe s as needed for fft plot calculate Nyquist frequency and compare with highest component freq. Note that the function calc_B_n vector is called but not provided. This function uses the function period, function type and number of terms to sum, as inputs. The outputs are the coefficient terms Bo and B" for the series, as well as the corresponding angular velocities . In addition, you must compare the component max frequency with the Nyquist frequency to ensure an accurate spectrum plot using FFT. Deliverables: Write an operable function calc_B_n vector and run your program to produce: a) Ramp (upward sloping saw-tooth) b) Triangle c) Square In addition, your code must print (display) the Nyquist and max frequency component! Finally, note that some parts of the main program are missing and must be re-written! In your code, all three series will sum the first 200 terms, have a fundamental period of two seconds, plot three full periods of the cycle and populate those three periods with a total of 4000 data-points