Matlab Questions: (Please write all the code and comments necessary; must include function)

___________________________________________________________________________________________________________________________________

_________________________________________________________________________________________________________________________________

______________________________________________________________________________________________________________________________

___________________________________________________________________________________________________________________________________

______________________________________________________________________________________________________________________________

______________________________________________________________________________________________________________________________

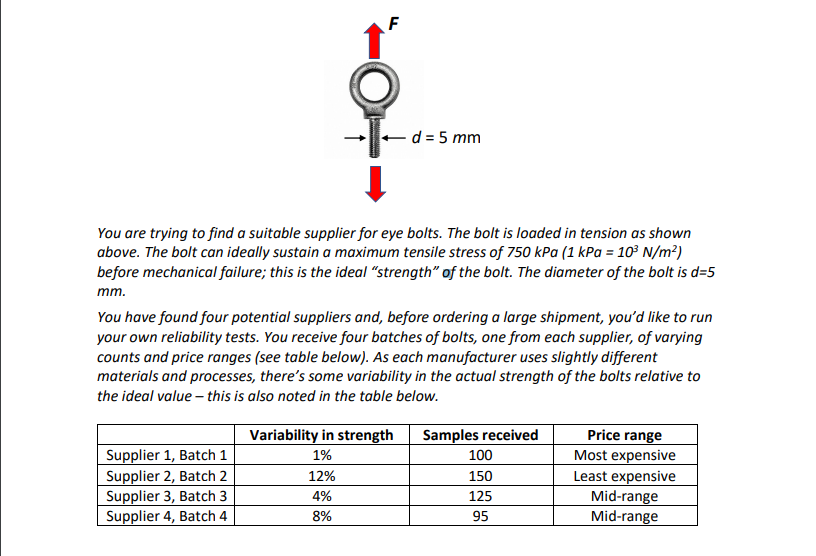
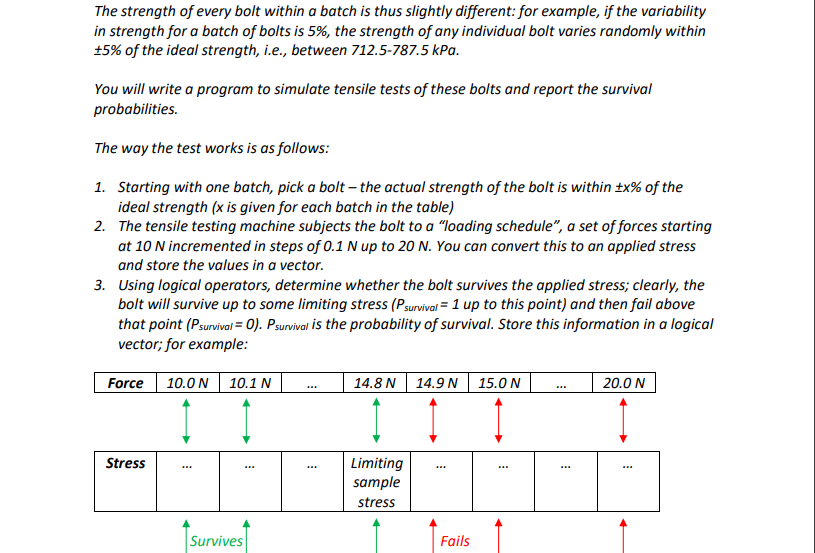
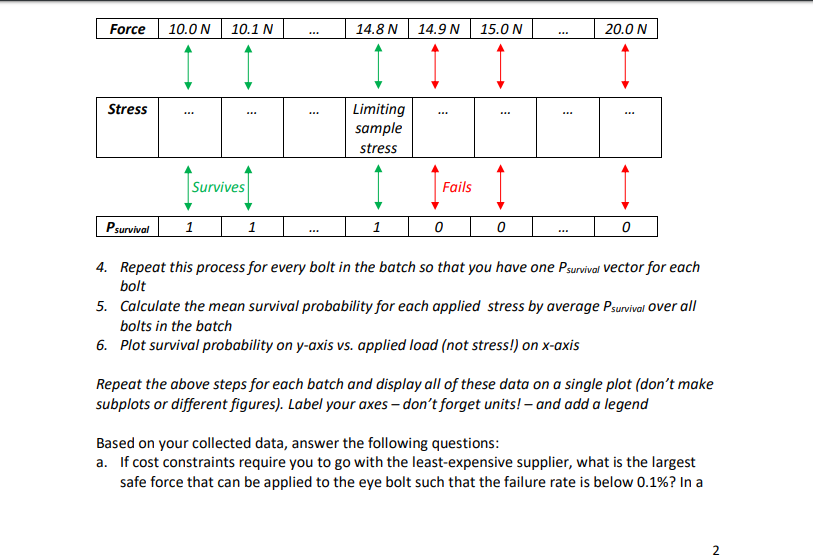
Suggested Outline of Code:

____________________________________________________________________________________________________________________________

_____________________________________________________________________________________________________________________________

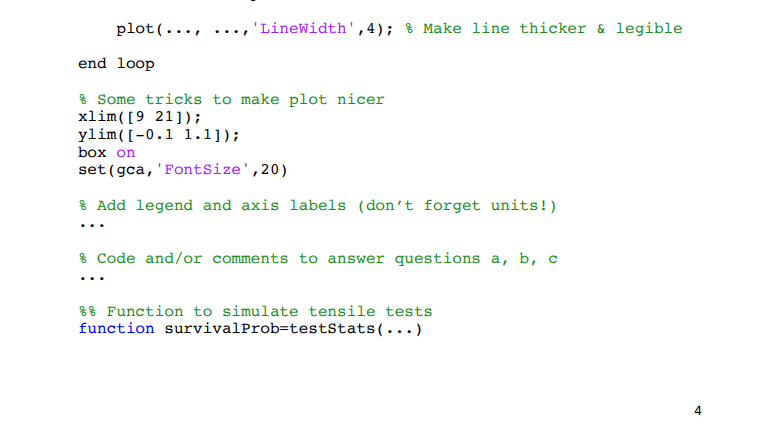
Homework 4 INSTRUCTIONS: PLEASE READ CAREFULLY Submit your code and descriptive answers in a single m-file. The m-file should be named as your initials and then underscore hw4, so for example my assignment would be "ar_hw4.m" You will generate one figure for this problem: please save this in PNG or PDF format only (on the figure window: file->save as->...). Name your image file yourinitials_hw4_img.png (e.g., ar_hw4_img.png) Use comments to distinguish between the various parts of the problem .mlx files are not acceptable and will be returned for conversion to.m files; text files and/or .mat files will receive a zero I have provided a skeleton of the code for you at the end of this document - you are not obliged to follow this to the letter but there must be a function within which the survival probability is calculated. No function 50% penalty! d = 5 mm You are trying to find a suitable supplier for eye bolts. The bolt is loaded in tension as shown 1 d = 5 mm You are trying to find a suitable supplier for eye bolts. The bolt is loaded in tension as shown above. The bolt can ideally sustain a maximum tensile stress of 750 kPa (1 kPa = 10 N/m) before mechanical failure; this is the ideal "strength" of the bolt. The diameter of the bolt is d=5 mm. You have found four potential suppliers and, before ordering a large shipment, you'd like to run your own reliability tests. You receive four batches of bolts, one from each supplier, of varying counts and price ranges (see table below). As each manufacturer uses slightly different materials and processes, there's some variability in the actual strength of the bolts relative to the ideal value - this is also noted in the table below. Supplier 1, Batch 1 Supplier 2, Batch 2 Supplier 3, Batch 3 Supplier 4, Batch 4 Variability in strength 1% 12% 4% 8% Samples received 100 150 125 95 Price range Most expensive Least expensive Mid-range Mid-range The strength of every bolt within a batch is thus slightly different: for example, if the variability in strength for a batch of bolts is 5%, the strength of any individual bolt varies randomly within +5% of the ideal strength, i.e., between 712.5-787.5 kPa. You will write a program to simulate tensile tests of these bolts and report the survival probabilities. The way the test works is as follows: 1. Starting with one batch, pick a bolt - the actual strength of the bolt is within x% of the ideal strength (x is given for each batch in the table) 2. The tensile testing machine subjects the bolt to a "loading schedule", a set of forces starting at 10 N incremented in steps of 0.1 N up to 20 N. You can convert this to an applied stress and store the values in a vector. 3. Using logical operators, determine whether the bolt survives the applied stress; clearly, the bolt will survive up to some limiting stress (Psurvival = 1 up to this point) and then fail above that point (Psurvival = 0). Psurvival is the probability of survival. Store this information in a logical vector, for example: Force 10.0N 10.1 N ... 14.8 N 14.9 N 15.0N | ... 20.00 Stress Limiting sample stress Survives Fails Force | 10.0 N | 10.1N | .. | 14.8 N | 14.9N | 15.0N | - | Stress Limiting sample stress Survives I Fails Fails 1 Psurvival 1 1 | 1 0 0 ... 0 4. Repeat this process for every bolt in the batch so that you have one Psurvival Vector for each bolt 5. Calculate the mean survival probability for each applied stress by average Psurvival over all bolts in the batch 6. Plot survival probability on y-axis vs. applied load (not stress!) on x-axis Repeat the above steps for each batch and display all of these data on a single plot (don't make subplots or different figures). Label your axes - don't forget units! - and add a legend Based on your collected data, answer the following questions: a. If cost constraints require you to go with the least-expensive supplier, what is the largest safe force that can be applied to the eye bolt such that the failure rate is below 0.1%? In a comment, compare this quantitatively to the maximum load (tensile force) that the bolt could ideally sustain? b. If the survival probability must exceed 95% at 14 N, which supplier(s)/batch(es) can you choose? C. Answer in a comment: how do you think process variability impacts reliability of a component in service? Stress = Force/Area of circular bolt cross-section Area of circle = Tid/4 1 kPa = 10 Pa = 10' N/m2 Appendix: Suggested outline of code % Mandatory headers (description, academic honesty, etc.) % Initialize data for component ...; % diameter in m ...; % bolt cross-sectional area ... ; & ideal strength in Pa & Set load schedule ...; $ forces ...; $stresses % Sample strength variability var = [...]; % percent variability in strength for each batch nSamp = [...]; % number of samples in each batch & Loop over all batches % Do not hard-code a value for the upper limit of the loop! begin loop % Call function test Stats % Pass to function: ideal strength, percent variability in strength for batch, number of samples in batch, applied stress vector % Get from function: vector of averaged survival Probabilities function call goes here... plot(..., ..., 'LineWidth',4); % Make line thicker & legible plot(..., ..., 'LineWidth',4); % Make line thicker & legible end loop % Some tricks to make plot nicer xlim( [921]); ylim((-0.1 1.1]); box on set (gca, 'FontSize',20) % Add legend and axis labels (don't forget units!) % Code and/or comments to answer questions a, b, c 8% Function to simulate tensile tests function survivalProb=testStats(...) % Inputs: ideal strength, percent variability in strength for batch, number of samples in batch, applied stress vector % Output: vector of averaged survival probabilities begin loop % Set actual limiting stress for sample Calculate survival probability vector for sample end loop % Perform averaging and return average survival probability vector to script end Homework 4 INSTRUCTIONS: PLEASE READ CAREFULLY Submit your code and descriptive answers in a single m-file. The m-file should be named as your initials and then underscore hw4, so for example my assignment would be "ar_hw4.m" You will generate one figure for this problem: please save this in PNG or PDF format only (on the figure window: file->save as->...). Name your image file yourinitials_hw4_img.png (e.g., ar_hw4_img.png) Use comments to distinguish between the various parts of the problem .mlx files are not acceptable and will be returned for conversion to.m files; text files and/or .mat files will receive a zero I have provided a skeleton of the code for you at the end of this document - you are not obliged to follow this to the letter but there must be a function within which the survival probability is calculated. No function 50% penalty! d = 5 mm You are trying to find a suitable supplier for eye bolts. The bolt is loaded in tension as shown 1 d = 5 mm You are trying to find a suitable supplier for eye bolts. The bolt is loaded in tension as shown above. The bolt can ideally sustain a maximum tensile stress of 750 kPa (1 kPa = 10 N/m) before mechanical failure; this is the ideal "strength" of the bolt. The diameter of the bolt is d=5 mm. You have found four potential suppliers and, before ordering a large shipment, you'd like to run your own reliability tests. You receive four batches of bolts, one from each supplier, of varying counts and price ranges (see table below). As each manufacturer uses slightly different materials and processes, there's some variability in the actual strength of the bolts relative to the ideal value - this is also noted in the table below. Supplier 1, Batch 1 Supplier 2, Batch 2 Supplier 3, Batch 3 Supplier 4, Batch 4 Variability in strength 1% 12% 4% 8% Samples received 100 150 125 95 Price range Most expensive Least expensive Mid-range Mid-range The strength of every bolt within a batch is thus slightly different: for example, if the variability in strength for a batch of bolts is 5%, the strength of any individual bolt varies randomly within +5% of the ideal strength, i.e., between 712.5-787.5 kPa. You will write a program to simulate tensile tests of these bolts and report the survival probabilities. The way the test works is as follows: 1. Starting with one batch, pick a bolt - the actual strength of the bolt is within x% of the ideal strength (x is given for each batch in the table) 2. The tensile testing machine subjects the bolt to a "loading schedule", a set of forces starting at 10 N incremented in steps of 0.1 N up to 20 N. You can convert this to an applied stress and store the values in a vector. 3. Using logical operators, determine whether the bolt survives the applied stress; clearly, the bolt will survive up to some limiting stress (Psurvival = 1 up to this point) and then fail above that point (Psurvival = 0). Psurvival is the probability of survival. Store this information in a logical vector, for example: Force 10.0N 10.1 N ... 14.8 N 14.9 N 15.0N | ... 20.00 Stress Limiting sample stress Survives Fails Force | 10.0 N | 10.1N | .. | 14.8 N | 14.9N | 15.0N | - | Stress Limiting sample stress Survives I Fails Fails 1 Psurvival 1 1 | 1 0 0 ... 0 4. Repeat this process for every bolt in the batch so that you have one Psurvival Vector for each bolt 5. Calculate the mean survival probability for each applied stress by average Psurvival over all bolts in the batch 6. Plot survival probability on y-axis vs. applied load (not stress!) on x-axis Repeat the above steps for each batch and display all of these data on a single plot (don't make subplots or different figures). Label your axes - don't forget units! - and add a legend Based on your collected data, answer the following questions: a. If cost constraints require you to go with the least-expensive supplier, what is the largest safe force that can be applied to the eye bolt such that the failure rate is below 0.1%? In a comment, compare this quantitatively to the maximum load (tensile force) that the bolt could ideally sustain? b. If the survival probability must exceed 95% at 14 N, which supplier(s)/batch(es) can you choose? C. Answer in a comment: how do you think process variability impacts reliability of a component in service? Stress = Force/Area of circular bolt cross-section Area of circle = Tid/4 1 kPa = 10 Pa = 10' N/m2 Appendix: Suggested outline of code % Mandatory headers (description, academic honesty, etc.) % Initialize data for component ...; % diameter in m ...; % bolt cross-sectional area ... ; & ideal strength in Pa & Set load schedule ...; $ forces ...; $stresses % Sample strength variability var = [...]; % percent variability in strength for each batch nSamp = [...]; % number of samples in each batch & Loop over all batches % Do not hard-code a value for the upper limit of the loop! begin loop % Call function test Stats % Pass to function: ideal strength, percent variability in strength for batch, number of samples in batch, applied stress vector % Get from function: vector of averaged survival Probabilities function call goes here... plot(..., ..., 'LineWidth',4); % Make line thicker & legible plot(..., ..., 'LineWidth',4); % Make line thicker & legible end loop % Some tricks to make plot nicer xlim( [921]); ylim((-0.1 1.1]); box on set (gca, 'FontSize',20) % Add legend and axis labels (don't forget units!) % Code and/or comments to answer questions a, b, c 8% Function to simulate tensile tests function survivalProb=testStats(...) % Inputs: ideal strength, percent variability in strength for batch, number of samples in batch, applied stress vector % Output: vector of averaged survival probabilities begin loop % Set actual limiting stress for sample Calculate survival probability vector for sample end loop % Perform averaging and return average survival probability vector to script end