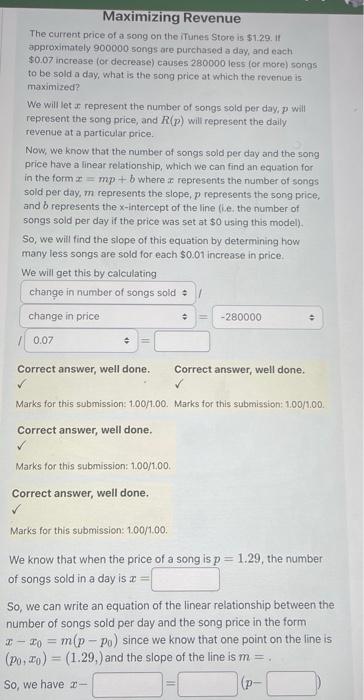
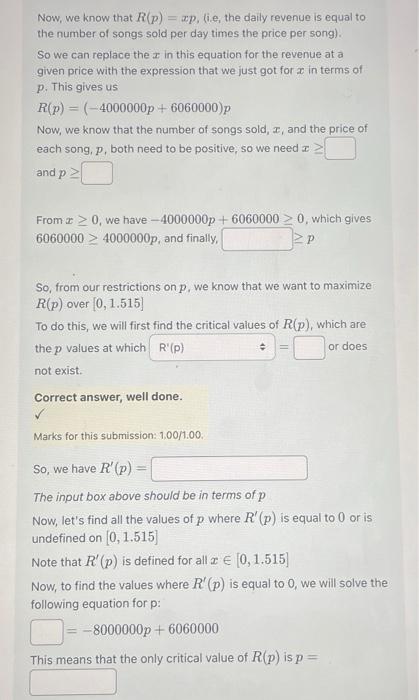
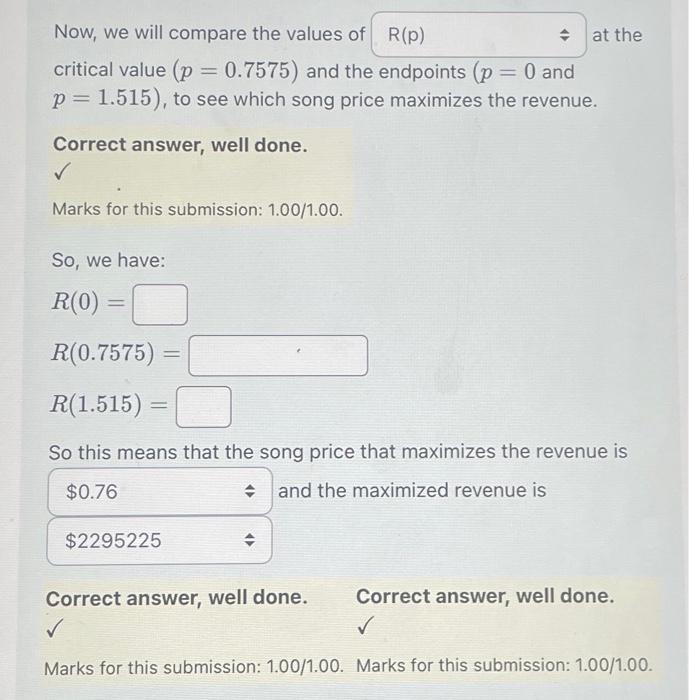
Maximizing Revenue The current price of a song on the iTunes Store is $1.29. If approximately 900000 songs are purchased a day, and each $0.07 increase (or decrease) causes 280000 less (or more) songs to be sold a day, what is the song price at which the revenue is maximized? We will let a represent the number of songs sold per day, p will represent the song price, and R(p) will represent the daily revenue at a particular price. Now, we know that the number of songs sold per day and the song price have a linear relationship, which we can find an equation for in the form mp+b where z represents the number of songs sold per day, m represents the slope, p represents the song price, and b represents the x-intercept of the line (ie. the number of songs sold per day if the price was set at $0 using this model). So, we will find the slope of this equation by determining how many less songs are sold for each $0.01 increase in price. We will get this by calculating change in number of songs sold change in price -280000 0.07 Correct answer, well done. Correct answer, well done. Marks for this submission: 1.00/1.00. Marks for this submission: 1.00/1.00. Correct answer, well done. Marks for this submission: 1.00/1.00. Correct answer, well done. Marks for this submission: 1.00/1.00. We know that when the price of a song is p=1.29, the number of songs sold in a day is = So, we can write an equation of the linear relationship between the number of songs sold per day and the song price in the form x-xo m(p-Po) since we know that one point on the line is (Po, xo) (1.29,) and the slope of the line is m = . So, we have 2- (p- Now, we know that R(p) = xp, (ie, the daily revenue is equal to the number of songs sold per day times the price per song). So we can replace the z in this equation for the revenue at a given price with the expression that we just got for in terms of p. This gives us R(p) (-4000000p + 6060000)p Now, we know that the number of songs sold, z, and the price of each song, p, both need to be positive, so we need and p From 0, we have-4000000p+ 6060000 6060000 4000000p, and finally, > 0, which gives P So, from our restrictions on p, we know that we want to maximize R(p) over [0, 1.515] To do this, we will first find the critical values of R(p), which are the p values at which R'(p) not exist. Correct answer, well done. Marks for this submission: 1.00/1.00. So, we have R'(p) The input box above should be in terms of p O or does Now, let's find all the values of p where R' (p) is equal to 0 or is undefined on [0, 1.515] Note that R' (p) is defined for all [0, 1.515] Now, to find the values where R' (p) is equal to 0, we will solve the following equation for p: : 8000000p+ 6060000 This means that the only critical value of R(p) is p= Now, we will compare the values of R(p) critical value (p = 0.7575) and the endpoints (p = 0 and p = 1.515), to see which song price maximizes the revenue. Correct answer, well done. Marks for this submission: 1.00/1.00. So, we have: R(0) = = R(0.7575) = R(1.515) = at the So this means that the song price that maximizes the revenue is $0.76 $2295225 and the maximized revenue is Correct answer, well done. Correct answer, well done. Marks for this submission: 1.00/1.00. Marks for this submission: 1.00/1.00.