May I know how to get part a and part d?
part D answer is attached below but i don't quite understand how to get the remaining 3 marks 
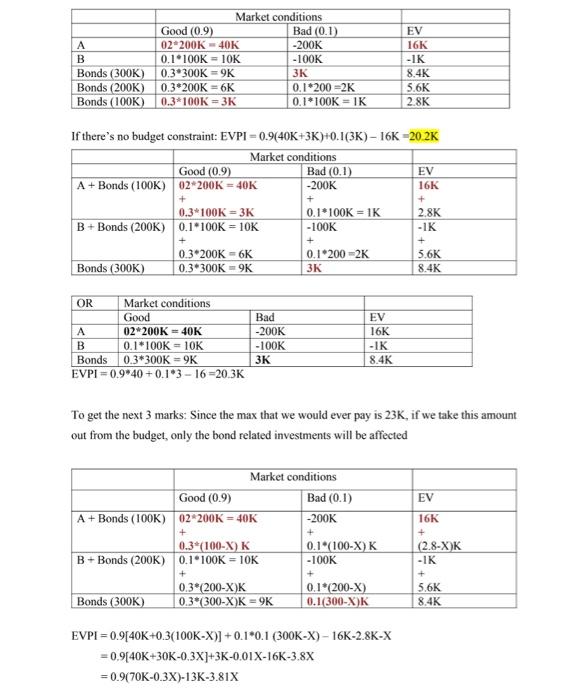
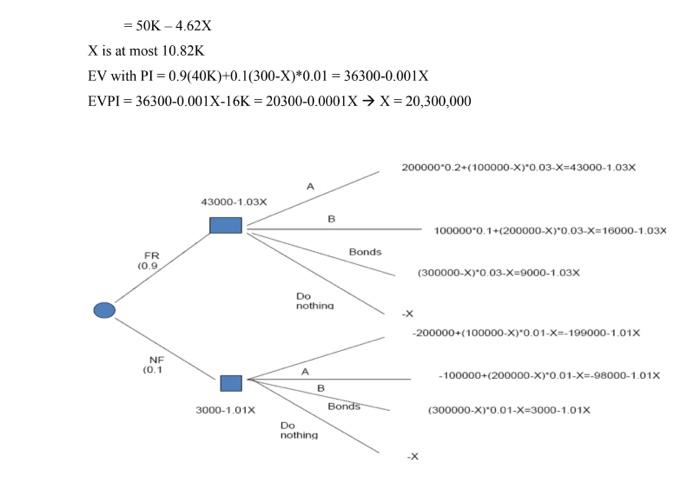
Question 4 (20 marks) Tedrick has $300,000 available in cash and he want to decide on how to invest this money. There are two main portfolios (collection of various financial instruments) that he can use for investment. The first portfolio Portfolio A, requires S200,000 of initial investment. If the market conditions turn out to be good then Portfolio A will bring 20% of interest. However, if the market conditions turn out to be bad, then he will lose the initial investment. The second portfolio Portfolio B, requires only $100,000 of initial investment. If the market conditions turn out to be good then Portfolio B will bring 10% of interest. However, if the market conditions turn out to be bad, then he will lose the initial investment. Because of regulatory reasons, he can only invest in one of the portfolios and only one unit of each portfolio. Besides these two portfolios, he can also use a safer option, investing in the bond market. This investment will bring 3% of interest if the market turns out to be good and only 1% of interest if the market turns out to be bad. He can invest as much as he want into the bond market up to his initial endowment S300,000 From his past experience, he estimates that the likelihood of having a good market is 0.90. a) Solve for the optimal investment decision (5 marks) b) Assume that he does not know the probability of having a good market (p). Provide a Toadmap for him for the optimal investment decision based on the good market probability (p). (4 marks) c) He can hire a consultant to conduct market survey to gather more information about the market situation. The consultant is to be paid $20,000. This reputable consultant tells him that, in the past, when the market was good (bad), they had predicted it correctly 90% (80%) of the cases. Solve for the optimal decision(s). (5 marks) if the consultant requires immediate payment, what is the maximum value that he may want to pay to consultant for perfect information about the state of the market (i.e. if the consultant suggests a good (bad) market then market will turn out to be good (bad) for sure.)? (Hint: The maximum value should be deducted from his budget of $300,000 at the beginning and he cannot invest in portfolio A or B if he does not have enough cash to meet the initial investment) (6 marks) Answer: Market conditions Good (0.9) Bad (0.1) A 02-200K-40K -200K B 0.1.100K = 10K -100K Bonds (300K) 0.38300K = 9K 3K Bonds (200K) 0.3 200K 6K 0.1*200 -2K Bonds (100K) 0.3*100K = 3K 0.1*100K - IK EV 16K -IK 8.4K 5.6K 2.8K EV 16K + If there's no budget constraint: EVPI = 0.9(40K+3K)+0.1(3K) - 16K=20.2K Market conditions Good (0.9) Bad (0.1) A+ Bonds (100K) 02*200K = 40K -200K 0.3*100K = 3K 0.1*100K = 1K 2.8K B+Bonds (200K) 0.1*100K = 10K -100K -IK 0.3.200K 6K 0.1.200 -2K 5.6K Bonds (300K) 0.3*300K -9K 3K 8.4K + + + + OR Market conditions Good A 02*200K - 40K 0.1*100K - 10K Bonds 0.3*300K = 9K EVPI=0.9*40 +0.183 - 16 =20,3K Bad -200K -100K EV 16K -IK 8.4K B To get the next 3 marks: Since the max that we would ever pay is 23K, if we take this amount out from the budget, only the bond related investments will be affected EV Market conditions Good (0.9) Bad (0.1) A + Bonds (TOOK) 02 200K = 40K -200K + 0.3* (100-X) K 0.1. (100-X)K B+Bonds (200K) 0.1*100K = 10K - 100K + 0.3*200-X)K 0.1*(200-X) Bonds (300K) 0.3*(300-X)K = 9K 0.1(300-X)K 16K + (2.8-X)K -IK + 5.6K 8.4K + EVPI=0.9[40K+0.3(100K-X)] +0.1*0.1 (300K-X) - 16K-2.8K-X = 0.9[40K+30K-0,3X3+3K-0.01X-16K-3.8X = 0.9(70K-0.3X)-13K-3.81X = 50K - 4.62X X is at most 10.82K EV with PI = 0.9(40K)+0.1(300-X)*0.01 = 36300-0.001X EVPI = 36300-0.001 X-16K = 20300-0.0001X X=20,300,000 200000 0.2+(100000-X)*0.03-X=43000-1.03% A 43000-1.03% B 1000000.1+(200000-X)*0.03-X=16000-1.03% Bonds FR (0.9 (300000-X)*0.03-X-0000-1.03% Do nothing -200000+(100000-X)*0.01-X=-199000-1.01% NE (0.1 A -100000+(200000-XX0.01-X=-98000-101x B 3000-1.01% Bonds (300000-X)*0.01-X=3000-1.01% Do nothing Question 4 (20 marks) Tedrick has $300,000 available in cash and he want to decide on how to invest this money. There are two main portfolios (collection of various financial instruments) that he can use for investment. The first portfolio Portfolio A, requires S200,000 of initial investment. If the market conditions turn out to be good then Portfolio A will bring 20% of interest. However, if the market conditions turn out to be bad, then he will lose the initial investment. The second portfolio Portfolio B, requires only $100,000 of initial investment. If the market conditions turn out to be good then Portfolio B will bring 10% of interest. However, if the market conditions turn out to be bad, then he will lose the initial investment. Because of regulatory reasons, he can only invest in one of the portfolios and only one unit of each portfolio. Besides these two portfolios, he can also use a safer option, investing in the bond market. This investment will bring 3% of interest if the market turns out to be good and only 1% of interest if the market turns out to be bad. He can invest as much as he want into the bond market up to his initial endowment S300,000 From his past experience, he estimates that the likelihood of having a good market is 0.90. a) Solve for the optimal investment decision (5 marks) b) Assume that he does not know the probability of having a good market (p). Provide a Toadmap for him for the optimal investment decision based on the good market probability (p). (4 marks) c) He can hire a consultant to conduct market survey to gather more information about the market situation. The consultant is to be paid $20,000. This reputable consultant tells him that, in the past, when the market was good (bad), they had predicted it correctly 90% (80%) of the cases. Solve for the optimal decision(s). (5 marks) if the consultant requires immediate payment, what is the maximum value that he may want to pay to consultant for perfect information about the state of the market (i.e. if the consultant suggests a good (bad) market then market will turn out to be good (bad) for sure.)? (Hint: The maximum value should be deducted from his budget of $300,000 at the beginning and he cannot invest in portfolio A or B if he does not have enough cash to meet the initial investment) (6 marks) Answer: Market conditions Good (0.9) Bad (0.1) A 02-200K-40K -200K B 0.1.100K = 10K -100K Bonds (300K) 0.38300K = 9K 3K Bonds (200K) 0.3 200K 6K 0.1*200 -2K Bonds (100K) 0.3*100K = 3K 0.1*100K - IK EV 16K -IK 8.4K 5.6K 2.8K EV 16K + If there's no budget constraint: EVPI = 0.9(40K+3K)+0.1(3K) - 16K=20.2K Market conditions Good (0.9) Bad (0.1) A+ Bonds (100K) 02*200K = 40K -200K 0.3*100K = 3K 0.1*100K = 1K 2.8K B+Bonds (200K) 0.1*100K = 10K -100K -IK 0.3.200K 6K 0.1.200 -2K 5.6K Bonds (300K) 0.3*300K -9K 3K 8.4K + + + + OR Market conditions Good A 02*200K - 40K 0.1*100K - 10K Bonds 0.3*300K = 9K EVPI=0.9*40 +0.183 - 16 =20,3K Bad -200K -100K EV 16K -IK 8.4K B To get the next 3 marks: Since the max that we would ever pay is 23K, if we take this amount out from the budget, only the bond related investments will be affected EV Market conditions Good (0.9) Bad (0.1) A + Bonds (TOOK) 02 200K = 40K -200K + 0.3* (100-X) K 0.1. (100-X)K B+Bonds (200K) 0.1*100K = 10K - 100K + 0.3*200-X)K 0.1*(200-X) Bonds (300K) 0.3*(300-X)K = 9K 0.1(300-X)K 16K + (2.8-X)K -IK + 5.6K 8.4K + EVPI=0.9[40K+0.3(100K-X)] +0.1*0.1 (300K-X) - 16K-2.8K-X = 0.9[40K+30K-0,3X3+3K-0.01X-16K-3.8X = 0.9(70K-0.3X)-13K-3.81X = 50K - 4.62X X is at most 10.82K EV with PI = 0.9(40K)+0.1(300-X)*0.01 = 36300-0.001X EVPI = 36300-0.001 X-16K = 20300-0.0001X X=20,300,000 200000 0.2+(100000-X)*0.03-X=43000-1.03% A 43000-1.03% B 1000000.1+(200000-X)*0.03-X=16000-1.03% Bonds FR (0.9 (300000-X)*0.03-X-0000-1.03% Do nothing -200000+(100000-X)*0.01-X=-199000-1.01% NE (0.1 A -100000+(200000-XX0.01-X=-98000-101x B 3000-1.01% Bonds (300000-X)*0.01-X=3000-1.01% Do nothing