May you explain all parts well! Especially the diagram , or I cant vote

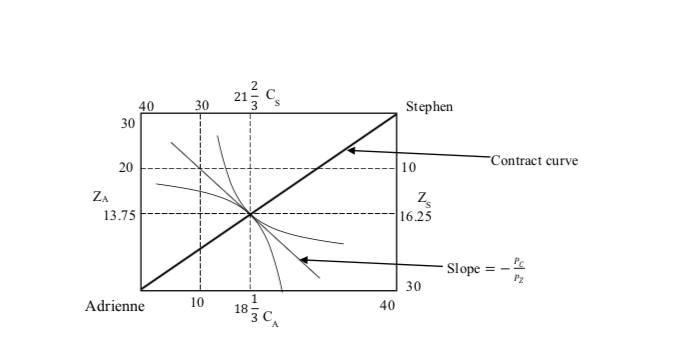
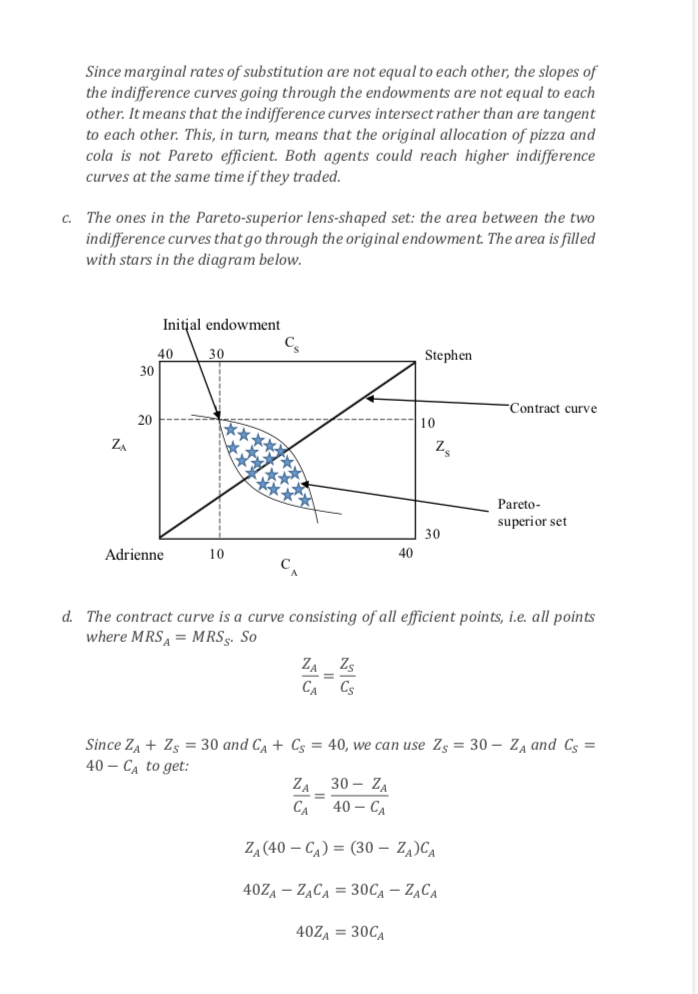
21 WIN C 40 30 Stephen 30 20 10 Contract curve ZA 13.75 16.25 Slope = Pz 30 Adrienne 10 18 40 WIH 3 C.3 ZA = CA Note than you can do the same thing from Stephen's perspective (Zs = = (s). The contract curve is a straight line with slope = 34 going through the origin. e. In equilibrium MRSA = MRSs = Pc/Pz. Moreover, we know that the equilibrium allocation is Pareto efficient, i.e. it lies on the contract curve. Since MRSA = CA = LA and ZA = = CA we get MRSA = = Pc/Pz. So the price ratio is 34, cola is cheaper than pizza. To find the final allocation we can use Adrienne's (or Stephen's) budget constraint. Currently her budget is 20Pz + 10Pc, after trade she will have ZAPz + CAPc. Setting these two equal to each other gives 20Pz + 10Pc = ZAPz + CAPc 20 + 10 PC = ZA + CA PZ Pc Since Pz e Pc = 3 and ZA = = CAwe have 20 + 10 . -= CA + CA . 55 NIW CA 2 55 CA = WIN 3 = 18 Therefore, ZA = =CA = = 13.75, Zs = 30 - 13.75 = 16.25, Cs = 40 - 18- = 21-. Note that the final allocation depends on the initial endowment because of the budget constraint. If we had a different initial endowment, the budget constraint would be different and the final allocation would be different as well.Since marginal rates of substitution are not equal to each other, the slopes of the indifference curves going through the endowments are not equal to each other. It means that the indifference curves intersect rather than are tangent to each other. This, in turn, means that the original allocation of pizza and cola is not Pareto efficient. Both agents could reach higher indifference curves at the same time if they traded. c. The ones in the Pareto-superior lens-shaped set: the area between the two indifference curves that go through the original endowment. The area is filled with stars in the diagram below. Initial endowment 30 Cs Stephen 30 Contract curve 20 10 ZA Pareto- superior set 30 Adrienne 10 40 C d. The contract curve is a curve consisting of all efficient points, i.e. all points where MRSA = MRSs. So ZA _ ZS CA Cs Since ZA + Zs = 30 and CA + Cs = 40, we can use Zs = 30 - ZA and Cs = 40 - CA to get: ZA 30 - ZA CA 40 - CA ZA (40 - CA) = (30 - ZA)CA 40ZA - ZACA = 30CA - ZACA 40ZA = 30CAAdrienne and Stephen consume pizza, 2, and cola, C. Adrienne's utility function is ii\" = ZACA, and Stephen's is U; = 235$\". Their endowments are 24 = 20, C4 = 10, Z, = 10, C, = 30. a. Draw an Edgeworth Box with the endowment allocation. What do we mean when we say that an allocation is feasible? Which allocations in the Bdgeworth box are feasible? b. What are the marginal rates of substitution for each person at the endowment point? Is the initial endowment Pareto efficient? For each agent sketch the indifference curves that go through the initial endowment point. c. Which allocations are Pareto-improving compared to the endowment allocation? d. Derive the contract curve formula. Add it to the graph e. What will the final allocation and the price ratio be if Adrienne and Stephen trade in a competitive market? Show them on the graph. ANSWER: a. The dimensions of the box are the quantities available of the goods, i.e. the sun'.I of endowmenls'. An allocation is feasible if and only if. {24 + 2,5 30 q+qsw Since the dimensions of the box are given by the sumI of the endowmenm all the allocations in the Edgeworth box are feasible. Moreover, all allocations inside the box also require that the above expressions hold with equality so the allocations are \"non- wasteful". _dZA_MUf_ZA_ZD_ 'ch'va'qm' dz, no; 0.52g-5c;-5 2, 1o 1