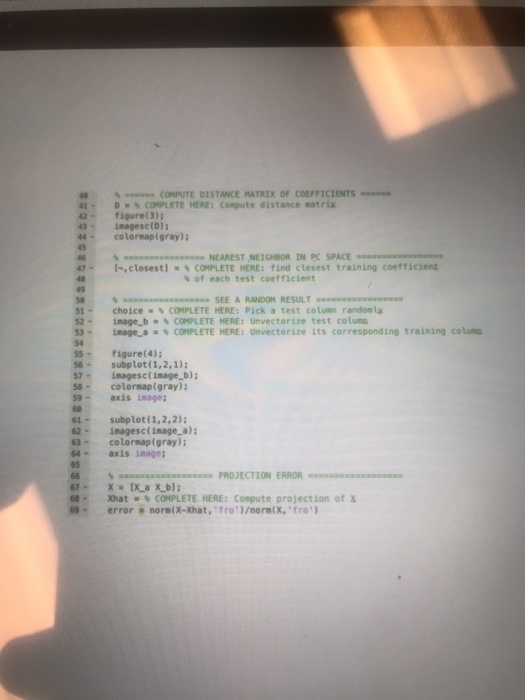
Mini-Project 6: Principal Component Analysis & Face Clustering DUE 04/23/2018 INSTRUCTOR: DANIEL. L.PIMENTEL-ALARCON In this mini-project you will use principal component analysis (PCA) to cluster imnges of hmman faces under varying illuminat ions. To this end we will use the Yale dataset (Yale data.sat), which includes the data array Images of size 48% 42 x 64 x 38, containing 2432 photos of 38 subjects (64 plotos per subject), nch photo of size 48 42. These imagrs look like: rl The msin intuition is that the vectorized photos of the sane subjects lie close to eachi other in the space of principal components, and so we will uwe a simple neanest neighbor approach on such space. (a) Let xy R2010 denote the jth vectorized photo of the ih subject, and let X e R30106x: 41 be the data matrix containing all the vectorized photos, Randomly split X into training data X, E R010x2 and testing data ?, e R2016 x228, in such a way that X. contains 58 images of each subject, and Xb contains 6 images of each subject. (b) let U, ?,V denote the singular value decomponition of X", such that X., U?VT. (o) The jh column of U deiotes the jh principal vector Display the 5(vectorinest) oaudling principal d) The disional entriew in ? denote the singular values. Plot their magnitudes How many of therm are (e) Let U, denote the matrix formed with the first r columns of U, where r is your answer from (d). This (f) Let e, E Rrx2204 be the coefficient matrix of Xa with rospect to Un such that x, = Ure,, and vectom, often called eigenfaces significant? way, U, spans the subspace containing most of the information of X. similarly for ,E R At this point we have transformed X, and X, into principal components space. More precisely, and e are the representation of Xa and X, with respect to the basis of principal vectors U,. Now we will classify Mini-Project 6: Principal Component Analysis & Face Clustering DUE 04/23/2018 INSTRUCTOR: DANIEL. L.PIMENTEL-ALARCON In this mini-project you will use principal component analysis (PCA) to cluster imnges of hmman faces under varying illuminat ions. To this end we will use the Yale dataset (Yale data.sat), which includes the data array Images of size 48% 42 x 64 x 38, containing 2432 photos of 38 subjects (64 plotos per subject), nch photo of size 48 42. These imagrs look like: rl The msin intuition is that the vectorized photos of the sane subjects lie close to eachi other in the space of principal components, and so we will uwe a simple neanest neighbor approach on such space. (a) Let xy R2010 denote the jth vectorized photo of the ih subject, and let X e R30106x: 41 be the data matrix containing all the vectorized photos, Randomly split X into training data X, E R010x2 and testing data ?, e R2016 x228, in such a way that X. contains 58 images of each subject, and Xb contains 6 images of each subject. (b) let U, ?,V denote the singular value decomponition of X", such that X., U?VT. (o) The jh column of U deiotes the jh principal vector Display the 5(vectorinest) oaudling principal d) The disional entriew in ? denote the singular values. Plot their magnitudes How many of therm are (e) Let U, denote the matrix formed with the first r columns of U, where r is your answer from (d). This (f) Let e, E Rrx2204 be the coefficient matrix of Xa with rospect to Un such that x, = Ure,, and vectom, often called eigenfaces significant? way, U, spans the subspace containing most of the information of X. similarly for ,E R At this point we have transformed X, and X, into principal components space. More precisely, and e are the representation of Xa and X, with respect to the basis of principal vectors U,. Now we will classify