Question
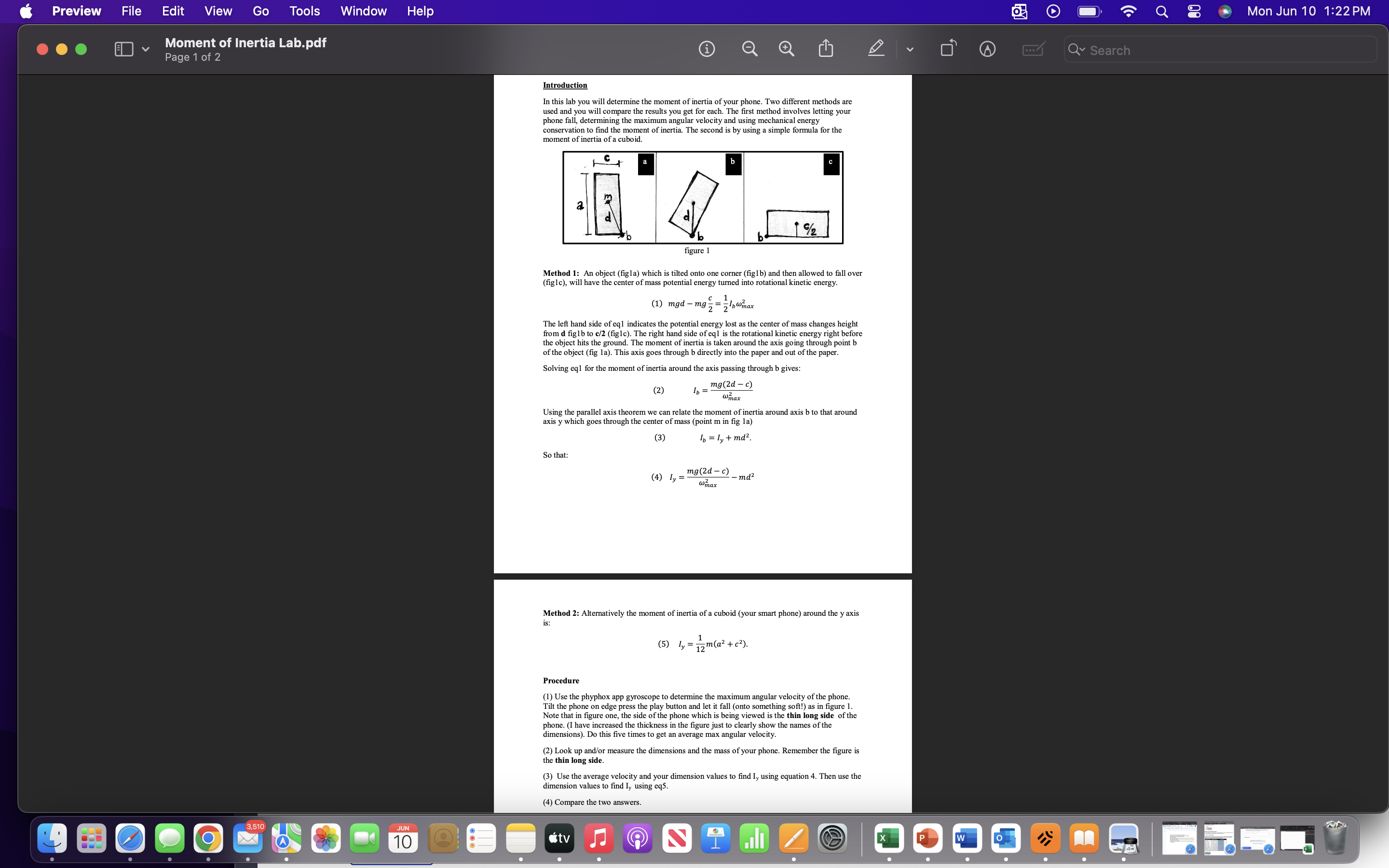
Moment of inertia of a smart phone Introduction In this lab you will determine the moment of inertia of your phone. Two different methods are
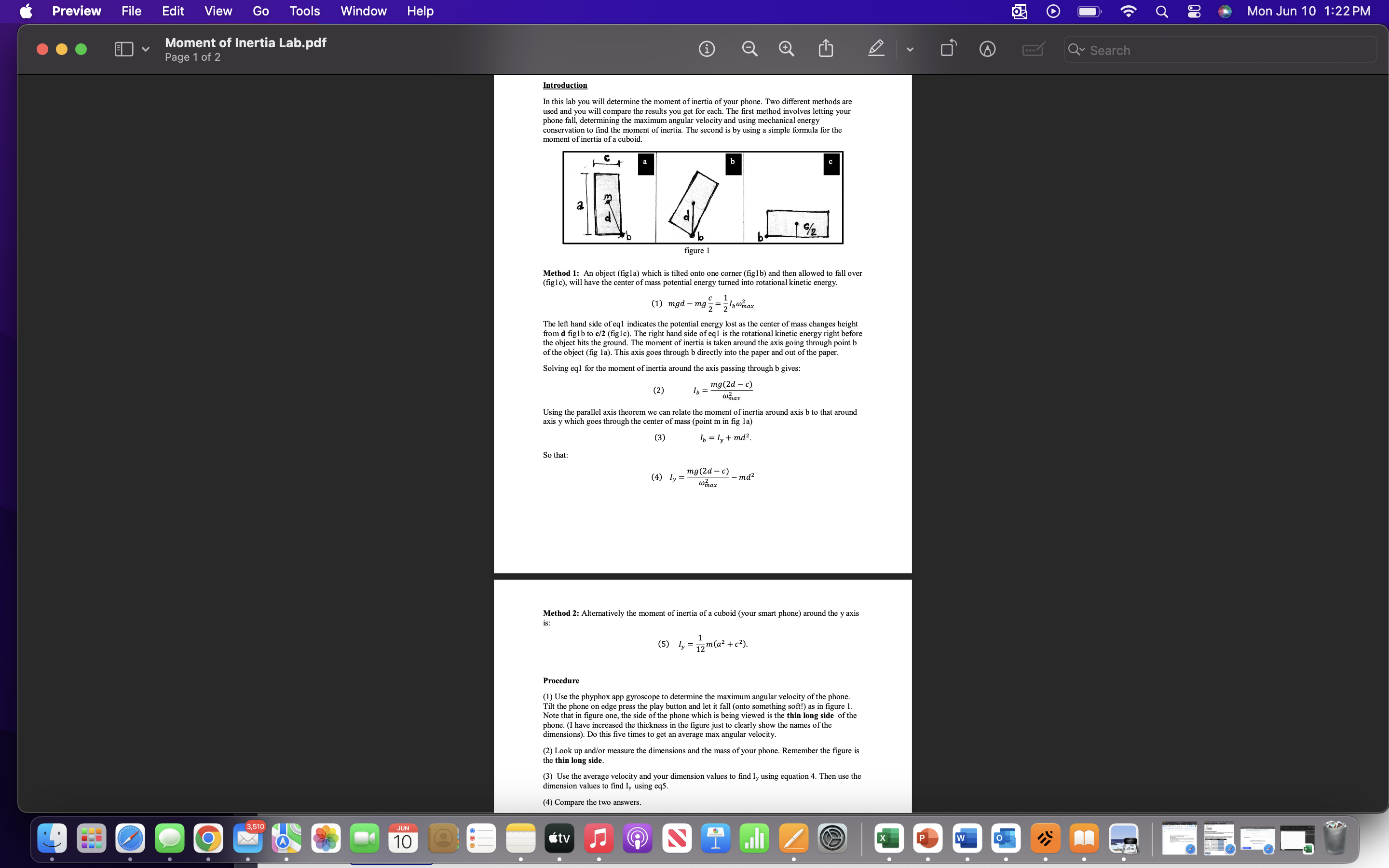
Moment of inertia of a smart phone Introduction In this lab you will determine the moment of inertia of your phone. Two different methods are used and you will compare the results you get for each. The first method involves letting your phone fall, determining the maximum angular velocity and using mechanical energy conservation to find the moment of inertia. The second is by using a simple formula for the moment of inertia of a cuboid. Method 1: An object (fig1a) which is tilted onto one corner (fig1b) and then allowed to fall over (fig1c), will have the center of mass potential energy turned into rotational kinetic energy. (1) ? 2 = 1 2 2 The left hand side of eq1 indicates the potential energy lost as the center of mass changes height from d fig1b to c/2 (fig1c). The right hand side of eq1 is the rotational kinetic energy right before the object hits the ground. The moment of inertia is taken around the axis going through point b of the object (fig 1a). This axis goes through b directly into the paper and out of the paper. Solving eq1 for the moment of inertia around the axis passing
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


