Question
Most major airlines allow passengers to carry two pieces of luggage?(of a certain maximum?size) onto the plane.?However, their studies show that the more?carry-on baggage passengers?have,
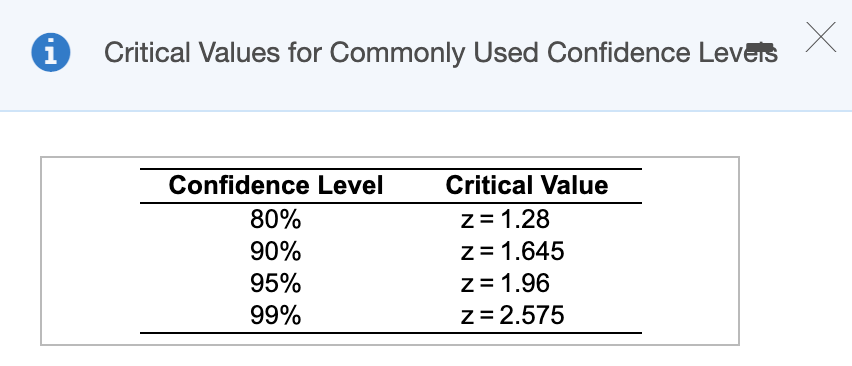
Most major airlines allow passengers to carry two pieces of luggage?(of a certain maximum?size) onto the plane.?However, their studies show that the more?carry-on baggage passengers?have, the longer it takes to unload and load passengers. One regional airline is considering changing its policy to allow only one?carry-on per passenger. Before doing?so, it decided to collect some data.?Specifically, a random sample of 1,000 passengers was selected. The passengers were?observed, and the number of bags carried on the plane was noted. Out of the 1,000 ?passengers, 380 had more than one bag. Complete parts a through d below.
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


