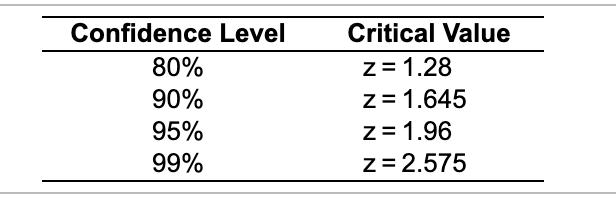
Most major airlines allow passengers to carry two pieces of luggage?(of a certain maximum?size) onto the plane.?However, their studies show that the more?carry-on baggage passengers?have, the longer it takes to unload and load passengers. One regional airline is considering changing its policy to allow only one?carry-on per passenger. Before doing?so, it decided to collect some data.?Specifically, a random sample of 1,000 passengers was selected. The passengers were?observed, and the number of bags carried on the plane was noted. Out of the 1,000 ?passengers, 380 had more than one bag. Complete parts a through d below.

Most major airlines allow passengers to carry two pieces of luggage (of a certain maximum size) onto the plane. However, their studies show that the more carry-on baggage passengers have, the longer it takes to unload and load passengers. One regional airline is considering changing its policy to allow only one carry-on per passenger. Before doing so, it decided to collect some data. Specically, a random sample of 1,000 passengers was selected. The passengers were observed, and the number of bags carried on the plane was noted. Out of the 1,000 passengers, 380 had more than one bag. Complete parts a through d below. 3 Click the icon to view a table of critical values for commonly used condence levels. a. Based on this sample, develop and interpret a 90% condence interval estimate for the proportion of the traveling population that would have been impacted had the one-bag limit been in effect. Determine the condence interval. (Round to three decimal places as needed. Use ascending order.) Which statement below correctly interprets the condence interval? A. There is 90% condence that the population proportion of passengers with more than one carry-on bag is in the interval. 0 B. There is a 0.90 probability that the sample proportion of passengers with more than one carry-on bag is in the interval. 0 0. Of all the possible population proportions of passengers with more than one carry-on bag, 90% are in the interval. 0 D. There is a 0.90 probability that the population proportion of passengers with more than one carry-on bag is in the interval. b. A certain plane has a capacity for 506 passengers. Determine an interval estimate of the number of passengers that you would expect to carry more than one piece of luggage on the plane. Assume the plane is at its passenger capacity. An interval estimate is from to passengers. (Round to the nearest whole number as needed.) c. Suppose the airline also noted whether the passenger was male or female. Out of the 1,000 passengers observed, 683 were female. Of this group, 226 had more than one bag. Using these data, obtain and interpret a 90% condence interval estimate for the proportion of female passengers in the population who would have been affected by the one-bag limit. Determine the condence interval. D D (Round to three decimal places as needed. Use ascending order.) Which statement below correctly interprets the condence interval? 0 A. There is 90% condence that the population proportion of female passengers with more than one carry-on bag is in the interval. 0 B. There is a 0.90 probability that the sample proportion of female passengers with more than one carry-on bag is in the interval. 0 0. Of all the possible population proportions of female passengers with more than one carry-on bag, 90% are in the interval. 0 D. There is a 0.90 probability that the population proportion of female passengers with more than one carry-on bag is in the interval. d. Suppose the airline decides to conduct a survey of its customers to determine their opinion of the proposed one-bag limit. The plan calls for a random sample of customers on different ights to be given a short written survey to complete during the ight. One key question on the survey will be: "Do you approve of limiting the number of carry-on bags to a maximum of one bag?" Airline managers expect that only about 20% will say "yes." Based on this assumption, what size sample should the airline take if it wants to develop a 90% condence interval estimate for the population proportion who will say "yes" with a margin of error of i 0.06? The airline should survey |:| passengers. (Round up to the nearest whole number as needed.)