Motorola used the normal distribution to determine the probability of defects and the number of defects expected in a production process. Assume a production process produces items with a mean weight of 10 ounces.
Calculate the probability of a defect in the following situations. Use Table 1 in Appendix B.
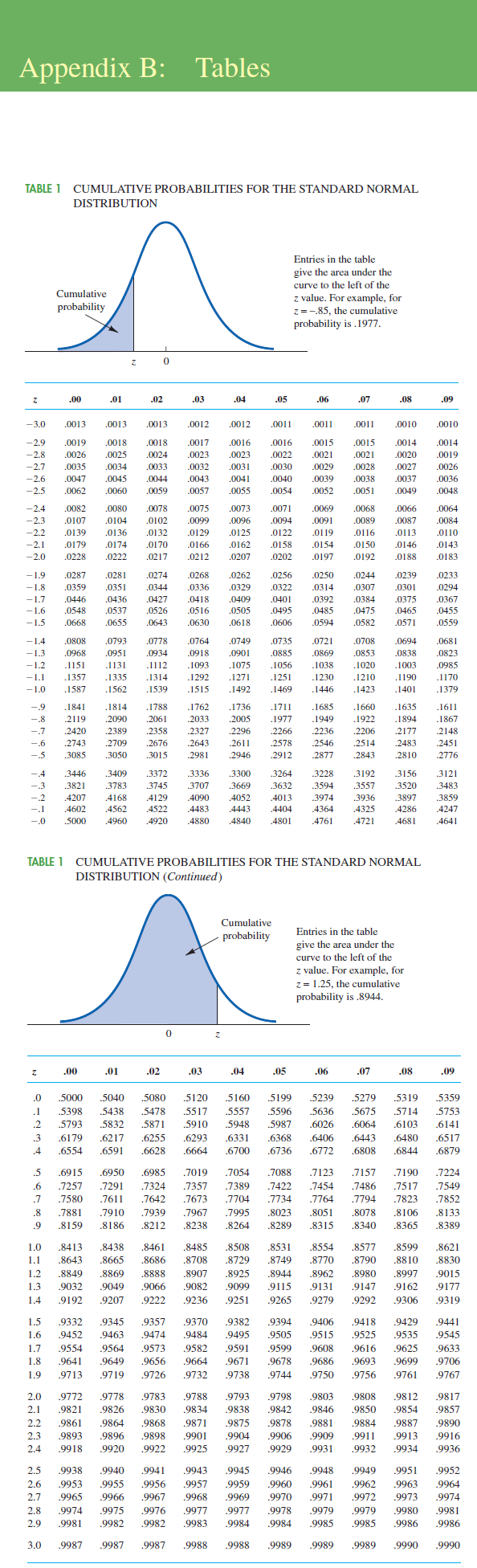
Appendix B: T bles IABLE 1 CUMU'LA'ITVE PROBABELJTEES FORTHE STANDARD NORMAL DISTRIBUTION En in 1.1:: table give the lama und' Illa ' curve. to Ihe lefl of 1112 CW9?" a value. For example, for mel'l'y a = .35, lhe cumulah've probability is .1977. Z .101 .01 .02 .03 .04 .05 .06 .07 .08 .09 73.0 .1103 13313 .11113 .0012 11112 .1111] .13)\" .0011 .IIIID 13110 729 .0019 .0013 .0318 .0017 .0016 .0016 .0015 .0015 .0014 .0014 2.3 8126 11115 .0124 .(X123 .1313 .13122 .(3121 .0321 .0320 .(3119 2.7 8135 11134 .0133 .(X132 .CIJ31 .13130 .(3129 .0323 .0027 .(3126 72.6 .11147 13345 .[IJ44 .(X143 .CIJ41 .m40 13139 13113 13337 13136 72.5 .11162 11160 .11159 .0057 13155 .11154 13152 11151 13349 13148 72.3 .0107 .0104 .0102. .0099 11196 .1194 18191 11139 11817 13134 722 .0139 .0136 .0132 .0129 .0125 .0122 .0119 .0116 .0113 .0110 21 .0179 .0174 .0170 .0166 .0162 .0158 .0154 .0150 .0146 .0143 20 .0228 .0222 .0217 .0212 .0207 .0202 .0197 .0192 .0188 .0183 7 1.9 .0287 .0281 .0274 .0268 .0262 .0256 .0250 .0244 .0239 .0233 7 1.8 .0359 .0351 .0344 .0336 .0329 .0322 .0314 .0307 .0301 0294 1.7 .0446 .0436 .0427 .041 8 .0409 .0401 .0392 .0334 .0375 .0367 1.6 .0543 .0537 .0526 .051 6 .0505 .0495 .0435 .0475 .0465 .0455 7 1.5 .0668 .0655 .1254] .0630 .06 I8 .[i .0594 .0532 .0571 .0559 1.4 .0808 .0793 .0778 .0764 .0749 .0735 .0721 .0708 .0694 .0681 1.3 0363 .0951 [F134 .0918 .0901 .0885 .0369 .0353 .0838 .0323 1.2 .1151 .1131 .1112 .1093 .1075 .1056 .1033 .1020 .1033 .0935 1.1 .1357 .1335 .1314 .1292 .1271 .1251 .1230 .1210 .1190 .1170 71.0 .1587 .1562 .1539 .1515 .1492 .1469 .1446 .1423 .1401 .1379 7.9 .1841 .1314 .1788 .1762 .1736 .1711 .1635 .1660 .1635 .1611 7.8 .2119 .2090 .2151 .2033 .2015 .1977 .1949 .1922 .1894 .1867 7.7 .2420 .2389 .2358 .2327 .2296 .2266 .2236 .2206 .2177 .2148 .6 .2743 .2709 .2676 .2643 .2611 .2578 .2546 .2514 .2483 .2451 .5 .3085 3050 .3015 .2981 .2946 .2912 .2877 .2843 .2810 .2776 7.4 3446 3409 .3372. .3336 33m .3264 .3228 3192 .3156 .3121 7.3 3821 3783 .3745 .3707 3669 .3632 .3594 3557 .3520 .3483 .2 .4207 .4 I 68 .4129 .4090 .4052 .4013 .3974 393-6 .3897 .3859 . 1 .4602 .4562 .45 22 .443 3 .4443 .4404 .43 64 .4325 . 428 6 .4247 7 .0 .5111] .4960 .4920 .4380 .4840 .4801 .476 1 .472 I .468 1 .464 1 '[ABLE 1 CUMULATIVE PROBABILIITES FORTHE STANDARD NORMAL DIST'RJBUTION (Comm) Emries in 0w. wble give the lama \"6661' 1112 curve to Ihe lefl of lhe a value. Forrexmnple, for z = 1.25, the cumulah've pmbnbility is .8944. z .011 .01 .02 .03 .04 .05 .06 .177 .08 .09 .0 .5000 .5040 .5080 .5120 .5160 .5199 .5239 .5279 .5319 .5359 .1 .5398 .5438 .5478 .5517 .5557 .5596 .5636 .5675 .5714 .5753 .2 .5793 .5832 .5871 .5910 .5948 .5987 6120.6 .6064 .6103 .6141 .3 .6179 .6217 .6255 .6293 .6331 .6368 .6406 .6443 .6480 .6517 .4 .6554 .6591 .6628 .6664 .6701) .6736 .6772 .6808 .6844 .6879 .5 .6915 .6950 .6985 .7019 .7054 .7088 .7123 .7157 .7190 .7224 .6 .7257 .7291 .7324 .7357 .7389 .7422 .7454 .7486 .75 1 7 .7549 .7 .7580 .7611 .7642 .7673 .7704 .7734 .7764 .7794 .7823 .7852 .8 .7881 .7910 .7939 .7967 .7995 .8023 .8051 .8078 .8106 .8133 .9 .8159 .8186 .8212 .8238 .8264 .8289 .8315 .8340 .8365 .8389 1.0 .8413 .8438 .8461 .8485 .8508 .8531 .8554 .8577 .8599 .8621 1.1 .8643 .8665 .8686 .8708 .8729 .8749 .8770 .8790 .8810 .8830 1.2 .8849 .8869 .8888 .8907 .8925 .8944 .8962 .8980 .8997 .9015 1.3 .9032 .9049 .9066 .9082 .9099 .9115 .9131 .9147 .9162 .9177 1.4 .91\" .9207 .9222 .m6 .925] .m5 .9279 .9292 .9306 .9319 1.5 .9332 .9345 .9357 .9370 .9382 .9394 .9406 .9418 .9429 .9441 1.6 .9452 .9463 .9474 .9484 .9495 .9505 .9515 .9525 .9535 .9545 1.7 .9554 .9564 .957 3 .95 82 .9591 .9599 .9608 .9616 .9625 .9633 1.8 .9641 .9649 .9656 .9664 .9671 .9678 .9686 .9693 .9599 .9706 1.9 .9713 .9719 .9726 .9732 .9738 .9744 .9750 .9756 .9761 .9767 2.0 .9772 .9778 .9783 .97 88 .9793 .9798 .9803 .9808 .9812 .9817 2.1 .9821 .9826 .9830 .9834 .9838 .9842 .9846 .9850 .9854 .9857 2.2 .9861 .9864 .9868 .9871 .9875 .9878 .9881 .9884 .9887 .9890 2.3 .9893 .9896 .9898 .9901 .9904 .9906 .9909 .9911 .9913 .9916 2.4 .9918 .9920 .9922 .9925 .9927 .9929 .9931 .9932 .9934 .9936 2.5 .9938 .9940 .9941 .9943 .9945 .9946 .9948 .9949 .9951 .9952 2.6 .9953 .9955 .9956 .9957 .9959 .9960 .9961 .9962 .9963 .9964 2.7 .9965 .9966 .9967 .9968 .9969 .9970 .9971 .9972 .9973 .9974 2.8 .9974 .9975 .9976 .9977 .9977 .9978 .9979 .9979 .9980 .9981 2.9 .9981 .9982 .9982 .9983 .9984 .9984 .9985 .9985 .9986 .9986 3.0 .9987 .9987 .9987 .9988 .9988 .9989 .9989 .9989 .9990 .9990