Mountain Paths - Part 2

Points

Points
10	Design
75	Running Program
15	Code Review
100	TOTAL

Submission

Design: Submit the PDF to GradeScope.

Source Code: Submit the source code to Vocareum

mountainpaths.cpp

functions.h (or functions.hpp)

functions.cpp

Objectives

Implement an algorithm from a description.

File I/O.

Using pass by reference and pass by const reference appropriately.

Working with parallel vectors.

Using pass by reference to modify multiple things in a function. Recall this is a RARE situation.

Overview

In this homework, you will extend Part 1 to compute some paths through the topographic terrain (mountains) as well as visualize these paths.

If you need a working version of Part 1, make a private post on piazza with your email address. We cannot give you credit for anything you submit for Part 1 after we send you the code. For Michael Nowaks sections, you will need to visit the instructor or TA during office hours, or schedule an appointment, to receive a working version of part 1.

Background

There are many contexts in which you may want to know the most efficient way to travel over land. When traveling through mountains (let's say you're walking), perhaps you want to take the route that requires the least total change in elevation with each step you take call it the path of least resistance. Given some topographic data, it should be possible to calculate a "greedy lowest-elevation-change walk" from one side of a map to the other.

Specifications

Design

Pseudocode/flowchart for greedy walk function.

Plan on how you will test to make sure the program works. Using test cases in autograder is not an appropriate response.

A Greedy Walk

A "greedy" algorithm is one that, in the face of too many possible choices to choose the best from, pursues a good solution to the problem one step at a time. At each step, a greedy algorithm makes a choice that seems best at that moment, without considering that this choice may make future steps less fruitful, achieving a final solution that may be good enough but not the best among all possible solutions. For example, assume you want to drive from city A to city B through highways that require payment of tolls with coins, and you dont have much cash with you (much less in coins!). You would like to take the route from A to B that minimizes the overall spending on toll fees. You could look at all routes you could take, how much each road in a route charges, and spend some time finding the overall best solution. If the route involves many possibilities, this can take quite a while. The greedy solution is simpler: at each time you have to choose a new highway, you select the one that charges less for the toll. It may be that you do very well with this strategy, but there is no guarantee it will work out well enough. It could be that you end up taking cheap roads that lead you to a very expensive area, where all following alternatives cost a lot, revealing that your greedy choices led to an expensive overall solution.

For the terrain maps that we are dealing with, we can envision a "walk" as starting in some cell at the left-most edge of the map (column 0) and proceeding forward by taking a "step" into one of the 3 adjacent cells in the next column over (column 1). (Well, if you are the top or bottom row of the region, you only have 2 possibilities, but unless your region is very small, most of the time you have 3 choices.) Note that steps can take you uphill or downhill. If you want to move from one side of the region to the other (lets say, from the west to the east edge of the region), there are way too many possible paths to consider: if n steps are necessary to traverse the region, the number of possible paths is close to 3n. For the maps you handled in Homework 4, for example the one with 480 rows and 480 columns, you have 480 possible rows to start your walk and you need 479 steps to get to the other side, resulting in approximately 480 * 3479 possible paths. This is a huge number, so considering each possible path when searching for a good solution (e.g., one that minimizes uphill movement) is a bad idea.

In the figure below, each cell contains the elevation data and the green cells highlight the path resulting from the greed strategy if we start at the 3rd row in the grid:

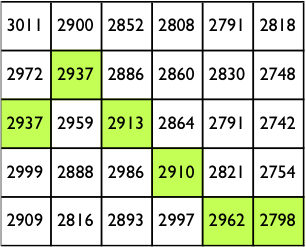
The diagrams illustrate a few rules for choosing where to move to at each step. In the case of a tie with the straight-forward position (east direction), you should always choose to go straight forward. In the case of a tie between the two non-forward locations, you should always choose the southeast movement (the one on bottom).

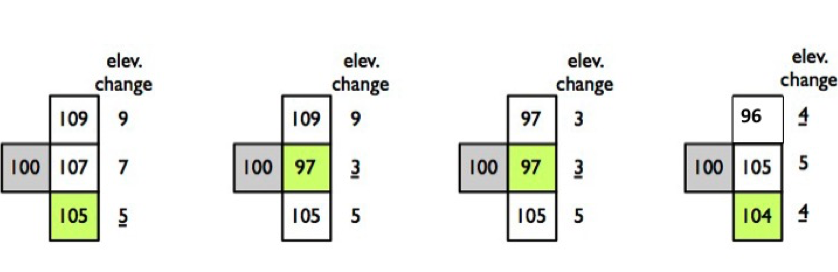
Case 1: smallest change is 5, go fwd-down

Case 2: smallest change is 3, go fwd

Case 3: smallest change is a tie (3), fwd is an option, so go fwd

Case 4: smallest change is a tie (4), go fwd-down

There are other ways to choose a path through the mountains while optimizing for vertical movement. Such algorithms (and their techniques and insights) are covered in other courses of a computer science degree.

Requirements

You implemented (as required by Part 1) code that read the topographical data from an input file, manipulated it to identify the appropriate gray scale value to display it, and generated an output file following a simple format to represent images.

For Homework Part 2, you need to compute all paths (from the west to the east side of the terrain) that follow the policy of path of least resistance. As you call the function creating each path, you will need to keep track of which is the shortest path. Then you will go back and call the function for that path again, painting it a different color. Well expect the output file generated by your program will produce a visualization similar to the ones depicted below. These are based on the sample input files from Part 1.

Program Flow

Your program starts by executing the first 3 steps from Part 1:

Read the data into a 2D vector

Find min and max elevation to correspond to darkest and brightest color, respectively

Compute the shade of gray for each cell in the map

In Part 1, you completed the assignment by producing the output file (image file in the PPM format) and used a tool to look at the visualization of your output.

For Part 2, your new steps are:

Step 4: Compute a greedy path

Write a function that calculates distance of the path created for a starting row and colors that path a particular color.

For a row, you color the cell you are at using the RGB color value passed in as three int parameters to the function, and compute your next position (following the specified movement rules) and color it, until you get to the last column. To choose the direction to move at each step, you look at the elevation data (that you read from a file) and compute the difference. Remember that you can be going downhill or uphill, therefore when you compute your vertical movement/distance, notice that it may end up negative, and you will need to compare the absolute value of vertical differences. As you color the path, you also have to compute the total distance. This is used to identify the best among all the greedy paths. You will need to return this distance at the end of the function.

The function will compute the greedy path starting at the given row and color it with the provided RGB color value, returning the total vertical movement. Every step you take should follow the greedy choice strategy we described (including what to do when there are ties.) As you move through the path, keep a running total of the total elevation change that would be 'experienced' by a person walking this path. Since we consider an elevation change the absolute value (i.e. going 'uphill' 10 meters is the same amount of change as going 'downhill' 10 meters), this running total will be non-decreasing and may end up being a pretty large positive number. The function should return this running total, so that you can compare it with other totals.

Greedy Function Requirements

The function declaration and definition should be placed in separate header and source files named functions.h (or functions.hpp) and functions.cpp. You may place other functions there as well.

The function signature/prototype is:

int colorPath(const vector>& heightMap, vector>& r, vector>& g, vector>& b, int color_r, int color_g, int color_b, int start_row);

1st parameter is the 2d vector of elevation data

2nd parameter is 2d vector of red values for an RGB color for the corresponding row,col location in the elevation data

3rd parameter is 2d vector of green values for an RGB color for the corresponding row,col location in the elevation data

4th parameter is 2d vector of blue values for an RGB color for the corresponding row,col location in the elevation data

5th parameter is the red value for the RGB path color. This color will replace the grey color of corresponding row,col locations of the path

6th parameter is the green value for the RGB path color. This color will replace the grey color of corresponding row,col locations of the path

7th parameter is the blue value for the RGB path color. This color will replace the grey color of corresponding row,col locations of the path

8th parameter is index of the starting row to begin procedure on.

Returns the distance of the path. This is the sum of changes in elevation from one column to the next.

Step 5: Call Function

Call the greedy algorithm function ( colorPath()) for each row (a loop works well). The greedy path should start on the west edge of the row (i.e. index 0) and color in red [RGB(252,25,63)] the corresponding cells in your output RGB data. While executing the loop, keep track of which row has the shortest path. If more than one path is shortest, then use the one with the lowest index.

Step 6: Paint shortest path

Call the function again for the row with the shortest path using this green [RGB(31,253,13)] for the color.

For extra credit: (NOT REQUIRED)

See details below. If you do not do this, your grade will not be affected negatively.

Read in two integers for row and column respectively.

Call a function that will paint the shortest path to the edge of the map going north, south, east, and west using a greedy algorithm. The color will be aqua [RGB(19,254,253)] . Function prototype given below.

Then you conclude by carrying out steps you already implemented in Part 1:

Produce the output file in the specified format (PPM) (You already did this in Part 1)

Use an online free tool to convert your PPM file into a JPG file

Extra Credit

For extra credit, after printing all paths and the shortest one, read two integers representing row and column from input.

Note: to prevent your program from hanging in the regular cases, you will need to check if there is still input in cin. You will then use a greedy algorithm as we did in Part II to paint four paths from the row, column location. Note, that your tiebreakers will vary according the the direction. Prefer forward over other directions, and forward and right after that.

Direction	Tiebreaker 1	Tiebreaker 2
north	N	NE
south	S	SW
east	E	SE
west	W	NW

The function signature is:

int colorPath(const vector>& heightMap, vector>& r, vector>& g, vector>& b, int color_r, int color_g, int color_b, int start_row, int start_col)

This overloaded function is similar to what you have already done, but will also specify which col to start on.

To prevent your program from hanging when testing regular test cases, you will need to see if there is more data in cin. If there is then you can get the row and column and proceed to call the extra credit function. Your code will look something like:

if(cin >> ec_row >> ec_column) { //ec for extra credit!

//call function to paint paths for point

}

So when testing, after you type in the filename also input the row and column on the same line before you hit enter. As long as you are not using getline() to get the filename, this will work.

Sample outputs below are based on the sample files from part one with the following (row, column) values.

(50,50)

(164, 382)

(164, 388)

3011 2900 2852 2808 2791 2818 2972 2937 2886 2860 2830 2748 2937 |2959 2913 28642791 2742 2999 2888 2986 2910 2821 2754 2909 2816 28932997 2962 2798 3011 2900 2852 2808 2791 2818 2972 2937 2886 2860 2830 2748 2937 |2959 2913 28642791 2742 2999 2888 2986 2910 2821 2754 2909 2816 28932997 2962 2798