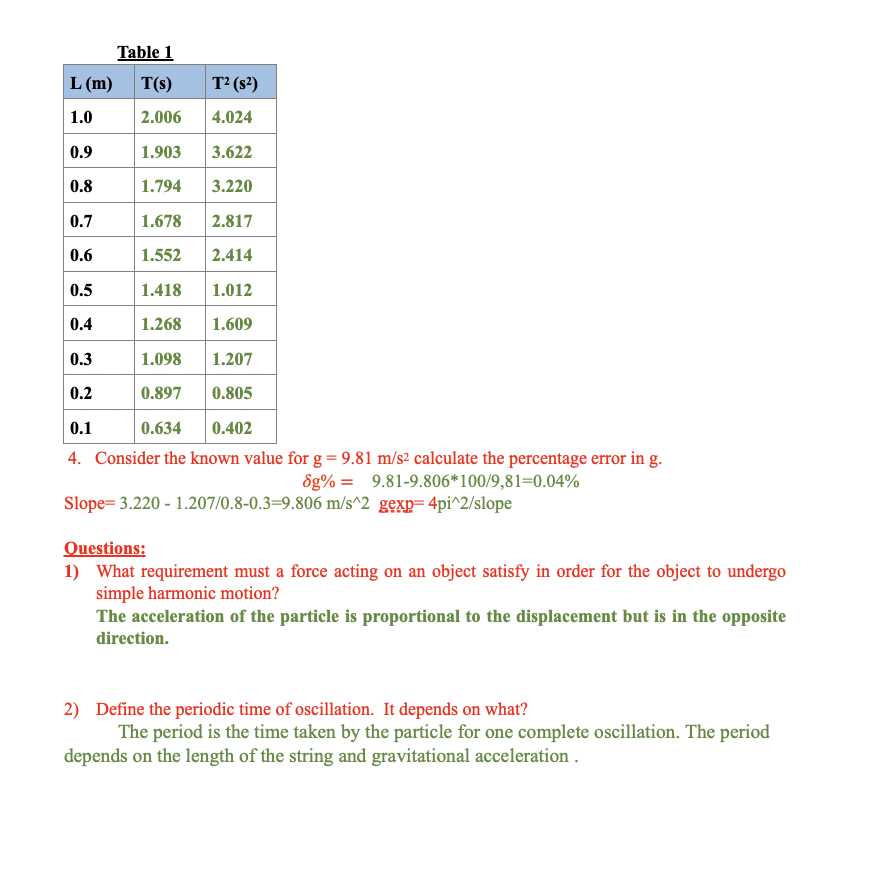
Name: AP Physics 1 Worksheet (Simple Harmonic Motion) Using Phet Interactive Simulation This activity consists of two parts. Part one: Simple Pendulum. Part two: Mass on a spring. To be familiar with simple harmonic motion, periodic time of an oscillation, angular velocity, the parameters that affect the oscillatory motion (length of the pendulum, the mass on a spring, the angle with the equilibrium position for simple pendulum and the distance from equilibrium position for mass on a spring) using Phet simulation, kindly, open the following links and play with them. For Simple Pendulum follow the link below. https://phet.colorado.edu/sims/html/pendulum-lab/latest/pendulum-lab_en.html For Mass on a Spring follow the link below. https://phet.colorado.edu/sims/html/masses-and-springs/latest/masses-and-springs_en.html Part I Simple Harmonic Motion (Simple Pendulum) Objectives: In this experiment the you can observe and study the periodic motion in a plane and investigate the relation between the period of a simple pendulum and its length. Also, the you can determine the acceleration due to gravity by this experiment. Theory: An ideal pendulum is a point mass (m) suspended at one end of a massless string with the other end of the string fixed as shown in Fig. 1. The motion of the system takes place in a vertical plane when the mass (m) released from an initial angle 0. The angular amplitude 0 is defined by the angle which the string makes with the vertical. The weight of the pendulum acts downward, and it can be resolved into two components. The component (mgcos!) is equal in magnitude to the tension n the string. The other component acts tangent to the arc along which the mgsine mass (m) moves. This component provides the force which drives the system. In equation form; the force (F) along the direction of motion is: mg + + F = - mg sine .....(1) For small values of the initial angle 0, the approximation Sino = tand = x//, can be used in equation 1, and then becomes mg x F = - ...(2) so, we can write according to Newton's second law: 1d2x mgx : + (3) m2 _ 1' (112 I The vibration of a pendulinn describes the simple harmonic motion (S.H.M.), the period (T) is given by l 4 2 T=2Jr => T2=E g g l (4) Where T: is the periodic time I: is the length from the point of suspension to the center of the bob. g: acceleration Qt: gravity. To satisfy the objective of this experiment, follovi.r the link below and do the following steps. httpsphet.colorado.edur'simsfhtmla'pendulum-labatesb'pendulum-lab en.html 1. Click on lab screen and use the length conn'oller to control the length ofthe pendulum (I), set I =1m. - Record the length intable 1. "\" u ,3 .. 2. Control the angle (click on the mass and drag along ' ' iii?\" 7' ' _ the protractor to x the angel), the angle must be . i very small (