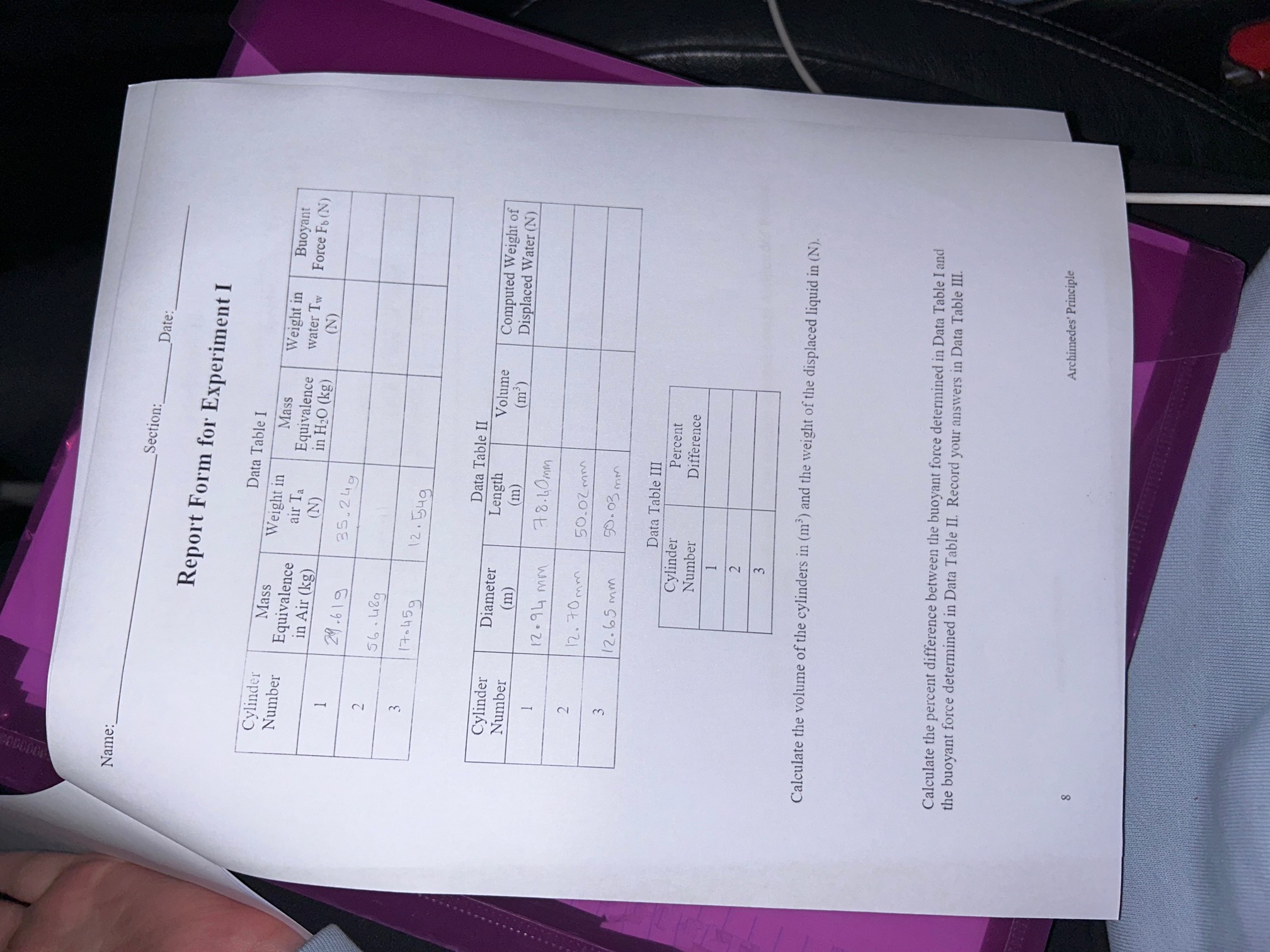
Name : Symara B Section: Date: Archimedes' Principle Objectives 1) To verify Archimedes' Principle by comparing the buoyant force on a submerged object and the weight of the fluid that it displaces. 2) To determine the density of a liquid using Archimedes' Principle. 3) To determine the density of an irregular object using Archimedes' Principle. Required Equipment and Supplies Quadruple Beam Balance Metal cylinders (3) Beakers Irregularly shaped object (White Rocks) Unknown liquid Copper Wire Vernier Caliper 50 ml volume flask Spring Scale/Force Probe Introduction Why does soap float on water? Why does a rock sink in water? Why does a hot air balloon rise? The answers to these and other similar questions lie in an understanding of the phenomena of buoyancy. Perhaps the most common experience that we as humans have of buoyancy is the feeling of "lightness" that we experience when we are partially or fully immersed in water. It appears that we have less weight. Appearances can be deceiving though, and in fact our weight is unchanged. The effect that we experience is a result of an additional force acting on our bodies. This force, usually called the buoyant force, is produced by the fluid and acts upward, opposite to the force of gravity. The force law that describes this force usually appears in the form of a principle known as Archimedes' principle after the 3rd century B.C Greek mathematician who first formulated an explanation of the phenomena of buoyancy. The principle as usually stated is A body wholly or partially immersed in a fluid is buoyed up by a force equal (in magnitude) to the weight of the displaced fluid. Archimedes' formulated the principle out of need to please his "employer" , the king, who wanted to find out if his crown was made of pure gold or some mixture of gold and other lesser metals. It turned out that the latter possibility was the case and Archimedes' was able to prove this using the above principle. It should be noted, however, that at the time of Archimedes' discovery Newton's laws were roughly 1900 years in the future and there was at best only a crude notion of what constituted a force, and even less of an Archimedes' PrincipleTest 3 Formula Sheet Test 3 Formula Sheet Name: Section: Date understanding of the effects produced by forces. We. on the other hand. will approach the study of buoyancy from a modern perspective, and apply Newton's laws to the phenomena we study. In modern language the principle states that if an object is immersed in a fluid such as water, there is an upwardly directed force that acts on the object that has a magnitude equal to the weight of the fluid that the object displaces. Thus, if the object displaces a volume of fluid V, and the fluid density (mass per unit volume) is p, then the buoyant force, Fo, acting on the object is Fi= pVg . Since m=pV. this is W another way of saying that Fo = mg where m is the mass of the Figure 1 displaced fluid. See Figure 1. Experiment I Consider the following situation where a metal cylinder is to be suspended from a wire that is attached to the Spring Scale. For our purposes we can think of the spring scale as a device that measures the tension in this wire. We will consider two cases. In the first case the cylinder is hung from the wire in the air, and in the second it is hung from the wire while submerged in a beaker of water. In the first case there are only two forces acting on the cylinder (if we assume that the buoyant effects of air are negligible). They are the downward force of gravity, I , W, (the weight of the cylinder) and the upward tension, Ta. Refer to Figure 2 for the free body diagram. With the cylinder in static equilibrium Newton's second law gives Ta - W=0 W or Figure 2 T, = W (1) where Ta is the tension in air and W the weight of the cylinder. When the cylinder is submerged in water we have an extra Iwit Four force: the upward buoyant force, Fow. Refer to Figure 3 for the free body diagram. Newton's second law now yields Tw - W+Fow = 0 W Figure 3 or IN = W-For (2) Archimedes' PrincipleTest 3 Formula Sheet Test 3 Formula Sheet A0 = ot Name: Section:_ Date: The buoyant force is, Fow, and the tension in water is, Tw. Notice that the weight is the same in each case but the tension (what the scale measures) is lower as a result of the buoyancy. So the "effective weight" is lower. That is. it acts like a lighter object even though the weight is unchanged. By combining (1) and (2) we find that For = Ta - In (3) Experiment II Recall that the buoyant force depends on the density of the liquid that the object is submerged in. The general equation for this relationship is Fo = pgV (4) Because of this fact, Archimedes' principle can be used to determine the density of a liquid. This can be accomplished by determining the buoyant force acting on a cylinder of known weight when it is submerged in two different liquids. Equation 3 is a result of combining equations 1 and 2. When the same object is submerged in an unknown liquid the buoyant force is defined as For = Ta- Tz (5) Using the relationship for the buoyant force defined in equation 4, a ratio of the buoyant force acting on an object in the unknown liquid. For, and the buoyant force acting on the object in water, Fow, can be developed. For _ PL Vg_PL (6) Fow PVg Pw This quantity, the ratio of the density of a substance to that of water is called the specific gravity of the substance. From equation 5 and 3 we can develop another expression for the specific gravity of a substance in terms of quantities which are measurable in the laboratory. For _ Ta- It Fow Ta - In Dividing the numerator and denominator by W, the result becomes, Fow 1-Iw/Ta Archimedes' PrincipleTest 3 Formula Sheet Test 3 Formula Sheet Name: Section: Date: The left side of this equation can be replaced by the results of equation 6. ( 7 ) Pir 1-I,, IT a It is the force probe reading when the object is submerged in the unknown liquid, Twis the force probe reading when the object is submerged in water and Ta is the weight of the object. Once these three values are measured, the specific gravity of the unknown liquid can be calculated using equation 7. Experiment III In Experiment I. we considered the effect of buoyancy on objects whose geometric shape conforms to some "neat" form such as a cylinder. Buoyancy affects objects of all shapes. and Archimedes' principle is valid for computing the buoyant force on an object of arbitrary shape. In this portion of the lab you will use Archimedes' principle to determine the specific gravity of an irregularly shaped object. This method was, in fact, used to determine the specific gravity of the rocks brought back from the moon by the Apollo astronauts. It is also the method that Archimedes' used to determine the specific gravity of the King's crown. And, in a sense, the formulation of Archimedes' principle was motivated by a need to solve this type of problem. Two measurements are required: the measured tension when the object is hung from the scale in air. Ta. which is approximately equal to the weight. and the measured tension when the object is hung from the scale while submerged in water, Tw. Using this data we can then determine the specific gravity of the object from the ratio of the two tensions Tw/Ta = (W- Fbw.)/W =1 - FowW =1 - puVg/pVg =1 - Pw/P Tw/Ta = 1 -1/S where S is the specific gravity of the object. Procedures Experiment I Equation 3 forms the basic foundation of our experiment, in that it allows for a determination of the buoyant force indirectly through measurements of the tensions, and Archimedes' PrincipleName: Section: Date: also it allows for the determination of the buoyant force independent of Archimedes' principle. So. it allows us to experimentally test Archimedes' principle! We will do this by comparing the measurements of the tension in the wire when the cylinder is suspended in air and when it is submerged in water. The value of the tension from the force probe is in Newton's so this value will require no conversion of units. 1) Hang the cylinder with a wire in air from the Quadruple Beam Balance. Ask for assistance from your lab instructor if necessary. Record the measured value for mass equivalence in kilograms in the Data Table I. Compute the appropriate weight in Newtons from the mass equivalence and record this value in Data Table I. 2) Repeat step 1) with the cylinder submerged in water. 3) Using equation 3 calculate the buoyant force. Record this value in Data Table I. 4) Measure the diameter and length of the metal cylinder with the vernier calipers in centimeters. Convert these measurements to meters and record them in Data Table II. 5) Calculate the volume of the cylinder in m'. Record this value in Data Table II. Convince yourself that because the cylinder was totally submerged, this is also the volume of water displaced by the cylinder. 6 Archimedes' principle states that the bouyant force is equal to the weight of the displaced fluid. Calculate the weight of the displaced fluid using F. = pVg where p = 1000kg/m' for water. Make sure the correct units are used for the volume and the acceleration due to gravity to obtain an answer in Newtons. Record this value for the buoyant force in Data Table II. 7) Calculate the percent difference between the value for buoyant force calculate in step 3 and step 6. Record this in Data Table I. 8) Repeat steps 1 thru 7 for two additional cylinders. Experiment II For this experiment the students are to use one of the cylinders from experiment I. 1) Hang the cylinder with a wire in the unknown liquid from the Quadruple Beam Balance. Using the measured value for mass in kilograms compute the appropriate weight in Newtons record this value in Data Table IV. 2) Repeat step 1) with the cylinder submerged in water. 3) Calculate the specific gravity of the unknown liquid using equation 7). Record this value in Data Table IV. 4) Using the specific gravity determine the density of the unknown liquid. Record this value in Data Table IV. 5) To check your result (and thus again verify Archimedes' principle), the student will determine the density of the liquid through direct measurement of the mass of a known volume of the liquid. 6) Record the volume of the flask in Data Table V. 7) Record the mass of the empty flask in Data Table V. 8) Completely fill the flask with the unknown liquid and determine the mass of the flask when it is full. Record this value in Data Table V. Archimedes' PrincipleTest 3 For Section: Date : Determine the mass of the unknown in the flask and record it in Data Table V. jo Determine the density of the unknown liquid and record it in Data Table V. 11) Determine the percentage difference of the density calculated using Archimedes' Principle and the density calculated using the direct method. Experiment III cond) The student will determine the specific gravity of an irregularly shaped object in this experiment. using Archimedes' Principle. 1) Hang the irregular object with a wire in air from the Quadruple Beam Balance. Using the measured value for mass in kilograms computed the weight in Newtons and record this value in Data Table VI. 2) Repeat step 1) for the irregular object completely submerged in water. 3) Calculate the specific gravity of the irregular object using equation 8). Record this value in Data Table VI. 4) Using the specific gravity determine the density of the irregular object. Record this value in Data Table VI. Questions 1) Draw free-body diagrams of an object a) hanging from a balance while immersed in water and b) hanging from a balance in air. 2) Describe the physical reason for the buoyant force in terms of pressure. 3) Distinguish between specific gravity and density. Archimedes' PrincipleName : Section:_ Date: 4) What would be the situation of an object immersed in a fluid if the object and the fluid had the same density? 5) Explain how a submarine is caused to submerge and surface without the use of its propulsion propeller. second) Archimedes' PrincipleName: Section: Date: Report Form for Experiment I Data Table I Cylinder Mass Weight in Number Mass Weight in Buoyant Equivalence air Ta Equivalence water Tw Force Fo (N) in Air (kg) (N) in H2O (kg) (N) 29. 6 1 9 35. 24g 56 . 489 17.45 0 2 . 549 Data Table II Cylinder Diameter Length Volume Computed Weight of Number m (m) (m') Displaced Water (N) 12: 94 mm 78.40 mm 12. 70 mm 50.02 mm 12.65 mm 50. 03 mm Data Table III Cylinder Percent Number Difference - N m Calculate the volume of the cylinders in (m') and the weight of the displaced liquid in ( N). Calculate the percent difference between the buoyant force determined in Data Table I and the buoyant force determined in Data Table II. Record your answers in Data Table III. Archimedes' PrincipleName: Section: Date: Report Form for Experiment II Data Table IV Cylinder Weight in water Weight in Number Specific Density of Tw (N) liquid TL (N) Gravity liquid (gm/cm') Data Table V Flask Volume Mass of Empty Mass of Full Mass of Liquid Density of (cm) Flask (gm) Flask (gm) (gm) liquid (gm/cm) per second) Show calculations for entries in Data Table IV and V. Calculate the percent difference of the densities calculated using Archimedes' Principle and the direct method. Archimedes' Principle