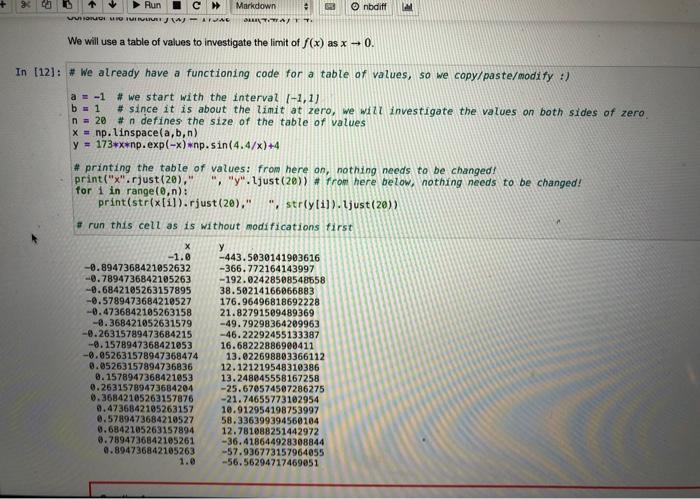
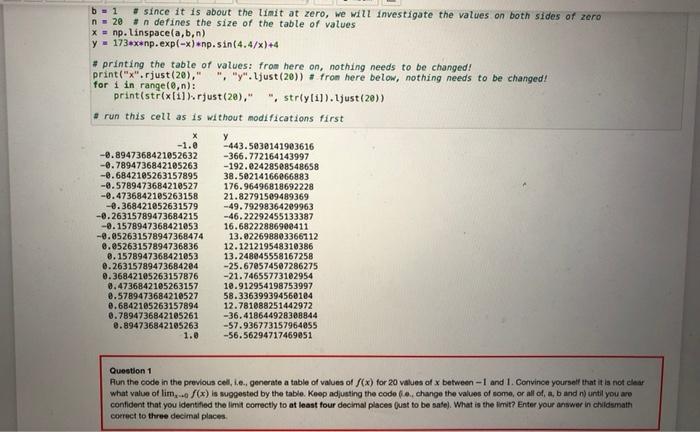
nbdift Run VUOMIOIMIVUURI Markdown CATWAL STIWA We will use a table of values to investigate the limit of f(x) as x -0. In [12]: # We already have a functioning code for a table of values, so we copy/paste/modify :) a = -1 # we start with the interval (-1,1) b1 # since it is about the limit at zero, we will investigate the values on both sides of zero n = 20 # n defines the size of the table of values X = np. linspace(a,b,n) y = 173*xxnp.exp(-x)wnp.sin(4.47x)+4 # printing the table of values: from here on, nothing needs to be changed print("x".rjust (20),"", "y". ljust (20)) # from here below, nothing needs to be changed! for i in range(0,n): print(str(x[i]).rjust (20)," ", stry[i]). ljust (20)) # run this cell as is without modifications first -1.6 -0.8947368421052632 -0.7894736842105263 -0.6842105263157895 -0.5789473684210527 -0.4736842105263158 -0.368421052631579 -0.26315789473684215 -0.1578947368421053 -0.052631578947368474 0.85263157894736836 8.1578947368421053 0.26315789473684204 6.36842105263157876 0.4736842105263157 0.5789473684210527 9.6842105263157894 9.7894736842105261 0.894736842105263 1.0 -443.5030141903616 -366.772164143997 -192.92428508548558 38.50214166066883 176.96496818692228 21.82791589489369 -49.79298364209963 -46.22292455133387 16.68222886900411 13.022698803366112 12.121219548310386 13.248045558167258 -25.670574507286275 -21.74655773102954 10.912954198753997 58.336399394560104 12.781088251442972 -36.418644928308844 -57.936773157964855 -56.56294717469951 b = 1 + since it is about the limit at zero, we will investigate the values on both sides of zero n = 20 n defines the size of the table of values x = np. linspace(a,b,n) y - 173ex np.exp(-x) np.sin(4.47x)+4 #printing the table of values: from here on, nothing needs to be changed! print("x".rjust (20)," ", "y". Ljust (20)) + from here below, nothing needs to be changed! for i in range(0,n): print(str(x(i)), rust(20)," ", stry[i]).just (20)) #run this cell as is without modifications First X y -1.0 -443.5038141903616 -8.8947368421052632 -366.772164143997 -@.7894736842105263 -192.02428508548658 -0.6842105263157895 38.50214166266883 -0.5789473684210527 176.96496818692228 -0.4736842105263158 21.82791509489369 -0.368421052631579 -49.79298364209963 -0.26315789473684215 -46.22292455133387 -0.1578947368421053 16.68222886908411 -0.052631578947368474 13.022698803366112 0.05263157894736836 12.121219548310386 0.1578947368421053 13.248045558167258 0.26315789473684204 -25.678574507286275 0.36842105263157876 -21.74655773102954 0.4736842105263157 18.912954198753997 0.5789473684210527 58.336399394560104 0.6842105263157894 12.781888251442972 0.7894736842105261 -36.418644928308844 0.894736842105263 -57.936773157964055 1.0 --56.56294717469851 Question 1 Run the code in the previous cell, i.e. generate a table of values of S(x) for 20 values of x between 1 and 1. Convince yourself that it is not clear what value of lim ...(x) is suggested by the table. Koop adjusting the codo o change the values of some or all of, a, b and n) until you are confident that you Identified the limit correctly to at least four decimal places just to be sate). What is the imit Enter your answer in childsmath correct to three decimal places nbdift Run VUOMIOIMIVUURI Markdown CATWAL STIWA We will use a table of values to investigate the limit of f(x) as x -0. In [12]: # We already have a functioning code for a table of values, so we copy/paste/modify :) a = -1 # we start with the interval (-1,1) b1 # since it is about the limit at zero, we will investigate the values on both sides of zero n = 20 # n defines the size of the table of values X = np. linspace(a,b,n) y = 173*xxnp.exp(-x)wnp.sin(4.47x)+4 # printing the table of values: from here on, nothing needs to be changed print("x".rjust (20),"", "y". ljust (20)) # from here below, nothing needs to be changed! for i in range(0,n): print(str(x[i]).rjust (20)," ", stry[i]). ljust (20)) # run this cell as is without modifications first -1.6 -0.8947368421052632 -0.7894736842105263 -0.6842105263157895 -0.5789473684210527 -0.4736842105263158 -0.368421052631579 -0.26315789473684215 -0.1578947368421053 -0.052631578947368474 0.85263157894736836 8.1578947368421053 0.26315789473684204 6.36842105263157876 0.4736842105263157 0.5789473684210527 9.6842105263157894 9.7894736842105261 0.894736842105263 1.0 -443.5030141903616 -366.772164143997 -192.92428508548558 38.50214166066883 176.96496818692228 21.82791589489369 -49.79298364209963 -46.22292455133387 16.68222886900411 13.022698803366112 12.121219548310386 13.248045558167258 -25.670574507286275 -21.74655773102954 10.912954198753997 58.336399394560104 12.781088251442972 -36.418644928308844 -57.936773157964855 -56.56294717469951 b = 1 + since it is about the limit at zero, we will investigate the values on both sides of zero n = 20 n defines the size of the table of values x = np. linspace(a,b,n) y - 173ex np.exp(-x) np.sin(4.47x)+4 #printing the table of values: from here on, nothing needs to be changed! print("x".rjust (20)," ", "y". Ljust (20)) + from here below, nothing needs to be changed! for i in range(0,n): print(str(x(i)), rust(20)," ", stry[i]).just (20)) #run this cell as is without modifications First X y -1.0 -443.5038141903616 -8.8947368421052632 -366.772164143997 -@.7894736842105263 -192.02428508548658 -0.6842105263157895 38.50214166266883 -0.5789473684210527 176.96496818692228 -0.4736842105263158 21.82791509489369 -0.368421052631579 -49.79298364209963 -0.26315789473684215 -46.22292455133387 -0.1578947368421053 16.68222886908411 -0.052631578947368474 13.022698803366112 0.05263157894736836 12.121219548310386 0.1578947368421053 13.248045558167258 0.26315789473684204 -25.678574507286275 0.36842105263157876 -21.74655773102954 0.4736842105263157 18.912954198753997 0.5789473684210527 58.336399394560104 0.6842105263157894 12.781888251442972 0.7894736842105261 -36.418644928308844 0.894736842105263 -57.936773157964055 1.0 --56.56294717469851 Question 1 Run the code in the previous cell, i.e. generate a table of values of S(x) for 20 values of x between 1 and 1. Convince yourself that it is not clear what value of lim ...(x) is suggested by the table. Koop adjusting the codo o change the values of some or all of, a, b and n) until you are confident that you Identified the limit correctly to at least four decimal places just to be sate). What is the imit Enter your answer in childsmath correct to three decimal places