need c++ format
below is my code for skiplist node.h and .cpp
*******************************************************************************
#include
using std::ostream;
class SkipListNode{
public:
SkipListNode(int newValue, int newNumberOfPointers);
int getValue(void);
int getNOP(void);
SkipListNode* getNext(int i);
void setNext(int i, SkipListNode* newnext);
ostream & write(std::ostream & outfile);
friend ostream & operator out, SkipListNode& node);
private:
int value;
int NumberOfPointers;
SkipListNode** next;
};
std::ostream& operator
*****************************************************************************************
#include
#include "SkipListNode.h"
using std::ostream;
SkipListNode::SkipListNode(int newValue,int newNumberOfPointers)
{
value = newValue;
NumberOfPointers = newNumberOfPointers;
next = new SkipListNode*[NumberOfPointers];
for (int i = 0; i
{
next[i] = nullptr;
}
this -> NumberOfPointers = NumberOfPointers;
}
int SkipListNode::getValue(void)
{
return value;
}
int SkipListNode::getNOP(void)
{
return NumberOfPointers;
}
SkipListNode*SkipListNode::getNext(int i)
{
return next[i];
}
void SkipListNode::setNext(int i, SkipListNode* newnext)
{
next[i] = newnext;
}
ostream & SkipListNode::write(std::ostream & outfile)
{
outfile
for (int i = 0; i
if (next[i] != nullptr){
outfile value
}
else{
outfile
}
}
return outfile;
}
std::ostream & operator
{
n.write(outfile);
return outfile;
}
*********************************************************************************

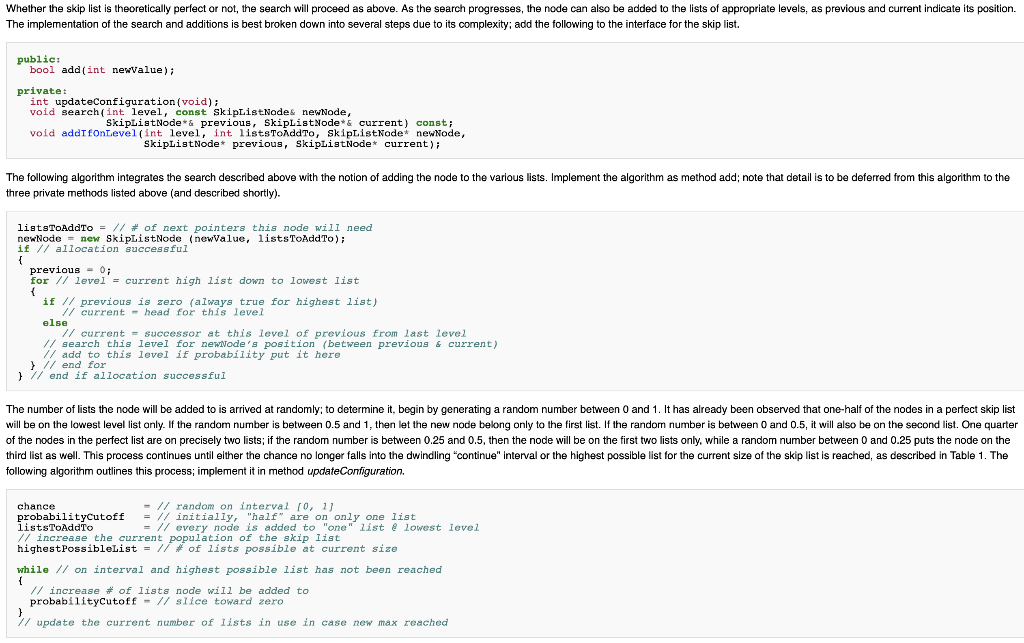



class SkipList public SkipList (void) private: int size int maxNumberofLists; int currentNumberofLists SkipListNode* heads: ti Adding to the Skip List Of course, creation and maintenance of a theoretically perfect skip list is prohibitively expensive. Instead, nodes are added in a statistical fashion to the list. Before going into the statistical details, consider again the theoretical skip list of Figure 1 and a search for the location for a node numbered 13.5. Pointers previous and current will be used to identify the section of the list that 13.5 would belong to. Initially, current will take on the value of the highest head pointer, which in this case points to node 16; previous begins as zero, as in the search of an ordinary linked list. In finding the location for 13.5, the following observations and actions would take lace observation action 16 is larger than 13.5 The search drops to level4 previous is still zero 8 is smaller than 13.5. 16 is larger than 13.5 current takes on the level 4 head, 8 previous becomes B and current becomes 16 The search drops to level 3 previous is not zero 12 is smaller than 13.5 16 is larger than 13.5 current takes on previous' successor, 12 previous becomes 12 and current becomes 16. The search drops to level 2 previous is not zero 14 is larger than 13.5 current takes on previous' successor, 14 The search drops to level 1 previous is not zero 13 is smaller than 13.5. 14 is larger than 13.5 current takes on its successor, 13 previous becomes 13 and current becomes 14 The search stops, as the lowest level has been reached Whether the skip list is theoretically perfect or not, the search will proceed as above. As the search progresses, the node can also be added to the lists of appropriate levels, as previous and current indicate its position. The implementation of the search and additions is best broken down into several steps due to its complexity; add the following to the interface for the skip list. public: bool add(int newValue) private: int updateConfiguration(void); void search(int level, const skipLstNode& newNode, SkipListNode& previous, SkipListNode*& current) const void addIfonLevel (int level, int listsToddTo, SkipListNode* newNode SkiplistNode* previous, SkiplistNode* current); The following algorithm integrates the search described above with the notion of adding the node to the various lists. Implement the algorithm as method add; note that detail is to be deferred from this algorithm to the three private methods listed above (and described shortly). 118tsToAddTo- // # of next pointers this node will need newNodenew SkipListNode (newValue, listsToAddTo) if // allocation successful previous0 for /levelcurrent high list down to lowest list f // previous is zero (always true for highest list) // currenthead for this level else /Tcurrent successor at this level of previous from last level /search this level for newwode's position (between previous¤t) // add to this level if probability put it here I/ end for /end if allocation successful The number of lists the node will be added to is arrived at randomly: to determine it, begin by generating a random number between 0 and 1. It has already been observed that one-half of the nodes in a perfect skip list will be on the lowest level list only. If the random number is between 0.5 and 1, then let the new node belong only to the first list. If the random number is between 0 and 0.5, it will also be on the second list. One quarter of the nodes in the perfect list are on precisely two lists; if the random number is between 0.25 and 0.5, then the node will be on the first two lists only, while a random number between 0 and 0.25 puts the node on the third list as well. This process continues until either the chance no longer falls into the dwindling "continue" interval or the highest possible list for the current size of the skip list is reached, as described in Table 1. The following algorithm outlines this process; implement it in method updateConfiguration. -Irandom on interval f0, 1 chance probabilityCutoff // initially, "half" are on only one list listsToAddTo // increase the current population of the skip Iist highestPossibleList = // # of lists possible at current size = // every node is added to "one" list @ lowest levci while // on interval and highest possible 1list has not been reached // increase # of lists node will be added to probabilityCutoff slice toward zero // update the current number of lists in use in case new max reached Searching any one level in the skip list for the new node's position proceeds in much the same fashion as the search of any single-level ordered linked list. In fact, the sole difference lies with the retrieval of a next pointer from a node; it must be the pointer to the next node on the current level. Implement the search in method searcfh. Once the position on a level has been found, the node is added to that level if the random number drawn earlier puts it there. Just as the search is very similar to that of a one-level list, so is the insertion. As might be expected, the difference lies in setting the next pointers of the previous and new nodes for the current level. Of course, if the previous pointer is zero, the head pointer for the current level is updated. Implement the addition in method addlfOnLevel Displaying the Skip List Since the display of a node shows the data of the node itself as well as the data of all of its next nodes, displaying a skip list can be accomplished as it would be in any ordinary list, following the pointers on level 0. Implement the display of the skip list in a method write for the class. Test the display of the skip list with the following extension to function main. static ofstream lout (lists.txt"; srand (2231) SkipList list; for (int n=1; n 1) if ((totalAdditions100) (totalAdditions 10000 && n100 == 0) (totalAdditions (n*log2 (n) + 0.5)
1) if ((totalAdditions100) (totalAdditions 10000 && n100 == 0) (totalAdditions (n*log2 (n) + 0.5)











