Need Detailed Solution on paper in 20 minutes i have there final answers each and everything is mentioned.

Nothing is missing each and every table amd related dataa is attached

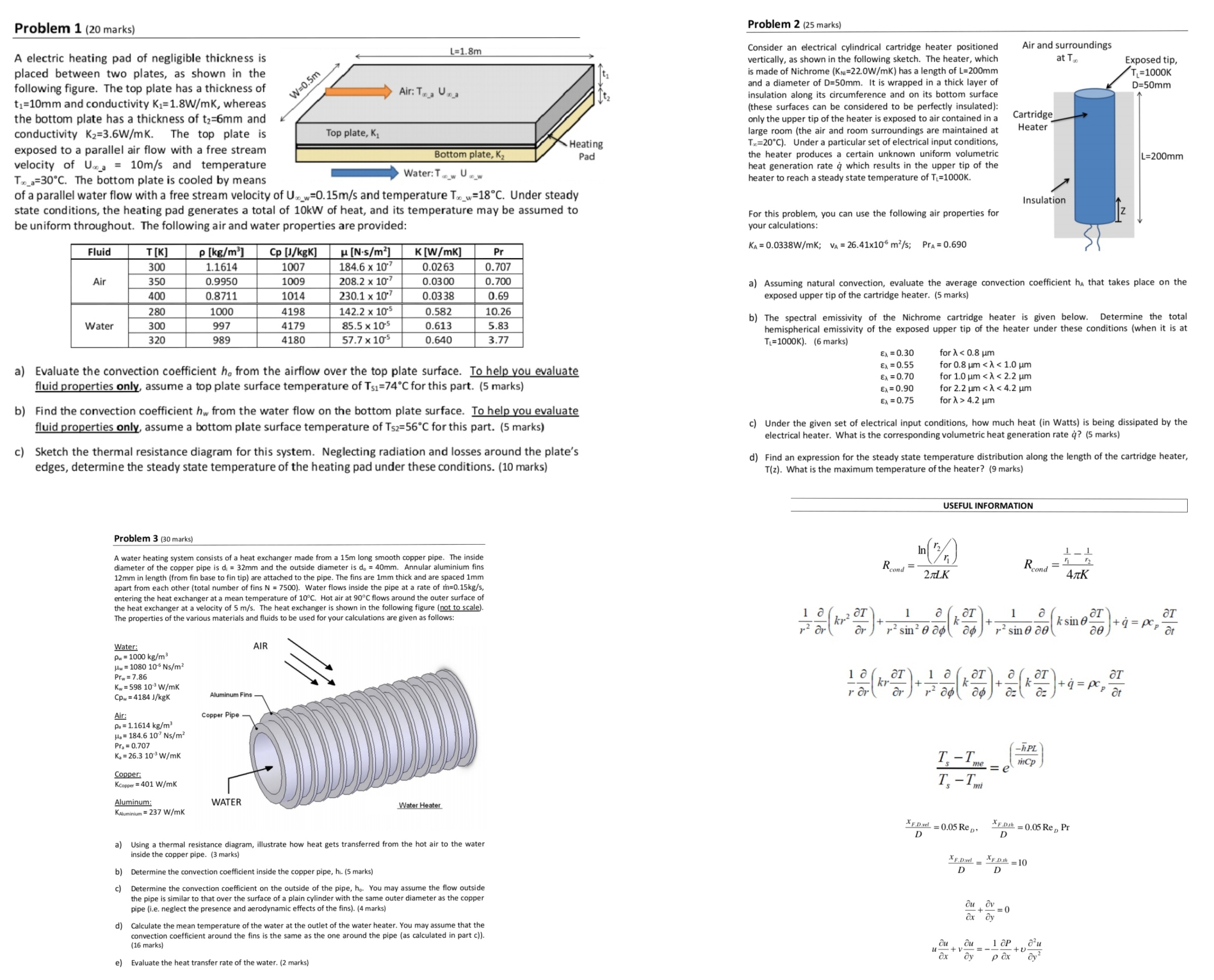
Problem 1 (20 marks) Problem 2 (25 marks) Air and surroundings A electric heating pad of negligible thickness is L=1.8m Consider an electrical cylindrical cartridge heater positioned vertically, as shown in the following sketch. The heater, which at To Exposed tip, placed between two plates, as shown in the is made of Nichrome (KN=22.0W/mK) has a length of L=200mm following figure. The top plate has a thickness of W =0.5m 1=1000K Air: To a Una and a diameter of D=50mm. It is wrapped in a thick layer of D=50mm ti=10mm and conductivity K1=1.8W/mk, whereas insulation along its circumference and on its bottom surface (these surfaces can be considered to be perfectly insulated): the bottom plate has a thickness of t2=6mm and only the upper tip of the heater is exposed to air contained in a Cartridge conductivity K2=3.6W/mk. The top plate is Top plate, K1 large room (the air and room surroundings are maintained at Heater exposed to a parallel air flow with a free stream Heating Tax=20"C). Under a particular set of electrical input conditions, Bottom plate, K2 velocity of U.. a = 10m/s and temperature Pad the heater produces a certain unknown uniform volumetric L=200mm T._a=30.C. The bottom plate is cooled by means Water: TW U._ heat generation rate q which results in the upper tip of the heater to reach a steady state temperature of Ti=1000K. of a parallel water flow with a free stream velocity of U.._w=0.15m/s and temperature T._w=18 C. Under steady state conditions, the heating pad generates a total of 10KW of heat, and its temperature may be assumed to Insulation For this problem, you can use the following air properties for be uniform throughout. The following air and water properties are provided: our calculations: Fluid T [K] P [kg/m'] Cp [J/kgK] M [N.s/m' ] K [W/mk] Pr KA = 0.0338W/mk; VA = 26.41x10 m?/s; Pra = 0.690 300 1.1614 1007 184.6 x 10' 0.02 63 0.707 Air 350 0.9950 1009 208.2 x 10" 0.03 00 0.700 a) Assuming natural convection, evaluate the average convection coefficient ha that takes place on the 400 0.8711 1014 230.1 x 10.7 0.03 38 0.69 exposed upper tip of the cartridge heater. (5 marks) 280 1000 4198 142.2 x 10-5 0.582 10.26 Water 300 997 4179 85.5 x 10-5 0.613 5.83 ) The spectral emissivity of the Nichrome cartridge heater is given below. Determine the total 320 989 hemispherical emissivity of the exposed upper tip of the heater under these conditions (when it is at 4180 57.7 x 10's 0.640 3.77 TL=1000K). (6 marks) Ex = 0.30 for A > 4.2 um 6) Find the convection coefficient hw from the water flow on the bottom plate surface. To help you evaluate fluid properties only, assume a bottom plate surface temperature of Ts2=56C for this part. (5 marks) ) Under the given set of electrical input conditions, how much heat (in Watts) is being dissipated by the electrical heater. What is the corresponding volumetric heat generation rate q? (5 marks) c) Sketch the thermal resistance diagram for this system. Neglecting radiation and losses around the plate's edges, determine the steady state temperature of the heating pad under these conditions. (10 marks) d) Find an expression for the steady state temperature distribution along the length of the cartridge heater, T(z). What is the maximum temperature of the heater? (9 marks) USEFUL INFORMATION Problem 3 (30 marks) A water heating system consists of a heat exchanger made from a 15m long smooth copper pipe. The inside diameter of the copper pipe is d = 32mm an s do = 40mm. Annular alumin Rcond = Roomd = 12mm in length (from fin base to fin tip) are attached to the pipe. The fins are 1mm thick and are spaced 1mm 2 TL.K ATK apart from each other (total number of fins N = 7500). Water flows inside the pipe at a rate of entering the heat exchanger at a mean temperature of 10"C. Hot air at 90C flows around the outer surface of the heat exchanger at a velocity of 5 m/s. The heat exchanger is shown in the following figure (not to scale). roperties of the various materials and fluids to be used for your calculations are given as follows: 1 0 2 dI 1 a OI 1 0 ksine OI ar ) r sin' 0 ad ("ag ) r sine ae(" Water AIR Pw = 1000 kg/m' Hw = 1080 10 Ns/m? Prw = 7.86 Kw = 598 10' W/mk Cp.= 4184 J/kgK Aluminum Fins - Air: Copper Pipe - P. = 1.1614 kg/m3 Ha = 184.6 107 Ns/m2 Pra = 0.707 K. = 26.3 103 W/mk -hPL inCp Copper: Is -me = e Kcopper = 401 W/mk T, - Im Aluminum: WATER KAluminium = 237 W/mk Water Heater XF.Dwl = 0.05 Rep. D * F.Dah = 0.05 Re, Pr D ) Using a thermal resistance diagram, illustrate how heat gets transferred from the hot air to the water inside the copper pipe. (3 marks) * F.Dvel =NF.D.sk = 10 Determine the convection coefficient inside the copper pipe, hi. (5 marks) D D Determine the convection coefficient on the outside of the pipe, he. You may assume the flow outside the pipe is similar to that over the surface of a plain cylinder with the same outer diameter as the copper pipe (i.e. neglect the presence and aerodynamic effects of the fins). (4 marks) ou OV = 0 ax dy d) Calculate the mean temperature of the water at the outlet of the water heater. You may assume that the convection coefficient around the fins is the same as the one around the pipe (as calculated in part c)). Olt + you _ _1 OP ax e) Evaluate the heat transfer rate of the water. (2 marks) pox dy?USEFUL INFORMATION (CONTINUED) Stefan Boltzmann Constant: 0 = 5.67 x 10 8 W/m2K* USEFUL INFORMATION (CONTINUED 100 TABLE 7.7 Summary of convection heat transfer correlations for external flow". 80 Correlation Geometry Conditions' 8 = 5x Re, 1/2 (7.19) Flat plate Laminar, T, Cfx = 0.664 Re, 1/2 (7.20) Flat plate Laminar, local, T, 60 Nu, = 0.332 Ref ppl (7.23 ) Flat plate Laminar, local, Ty, Pr 2 0.6 n, (%) 1 = 12/r ] 8, = 8 Pr-1/3 (7.24) Flat plate Laminar, T 40 Cy. = 1.328 Re, 172 (7.29) 2 3 Flat plate Laminar, average, T's Nu, = 0.664 Ref prl (7.30) Flat plate Laminar, average, Ty. Pr 2 0.6 20 = 2 + 1/2 Nu, = 0.564 Peln (7.32) Laminar, local, T,, Pr $ 0.05, Pe, 2 100 20 4 =L+12 Flat plate Ap = Let Cf.x = 0.0592 Re, Us (7.34) Flat plat Turbulent, local. T,, Re, $ 10' 8 = 0.37x Re, V (7.35) Flat plate Turbulent, Ty, Re, $ 10' Nu, = 0.0296 Revs prl (7.36) Flat plate 0 .5 1.0 2.5 Turbulent, local, T,, Re, $ 10. L:R2(hulkA )12 1.5 2.0 0.6 S Pr $ 60 Cuz. = 0.074 Re, 15 - 1742 Rez' (7.40) Flat plate Mixed, average, Ty, Rexe = 5 X 105, FIGURE 3.19 Efficiency of annular fins of rectangular profile. Rel $ 10' Vuz = (0.037 Regs - 871)Pr (7.38) Flat plate Table 12.1 Blackbody Radiation Functions f(2) Mixed, average, Ty, Rete = 5 X 10', tel $ 10', 0.6 5 Pr $ 60 AT [um K] F(A AT [um K] F(X) Nup = C Rep Prl (7.52) Cylinder (Table 7.2) Average, T,, 0.4 S Rep $4 X 10', 200 0.000000 3200 0.318102 Pr 2 0.7 40 0.000000 Nup = C Reg Pr(PrlPr,) 1/4 (7.53) 3400 0.361735 Cylinder (Table 7.4) Average, To, 1 5 Rep $ 10', 0.7 S Pr s 500 600 0.000000 3600 0.403607 Nup = 0.3 + 10.62 Reb pr3 Cylinder Average, T,. Rep Pr 2 0.2 800 0.000016 3800 0.443382 X [1 + (0.4/Pr)23 ]-V/4] 0.000321 X [1 + (Rep/282,000)$78 jars (7.54) 1000 4000 0.480877 Nup = 2 + (0.4 Reg 1200 0.002134 4200 0.516014 Sphere Average, T., 3.5 = Rep $ 7.6 X 10', + 0.06 Rep )Pr 0.71 S Pr s 380, 1.0 5 (1/Ms) $ 3.2 1400 0.007790 1400 0.548796 (7.56) 1600 0.019718 4600 0.579280 TABLE 7.2 Constants of Equation 1800 0.039341 4800 0.607559 7.44 for the circular cylinder in 2000 0.066728 5000 0.633747 cross flow [11, 12] 2200 0.100888 5200 0.658970 Rep 2400 0.140256 5400 0.680360 04-4 0.989 0.330 4-40 0.911 0.385 2600 0.183120 40-4000 0.683 0.466 2800 0.227897 4000-40,000 0.193 0.618 3000 0.273232 40,000-400,000 0.027 0.805 USEFUL INFORMATION (CONTINUED) TABLE 8.4 Summary of convection correlations for flow in a circular tube"be Correlation Conditions f = 64/Rep (8.19) Laminar, fully developed USEFUL INFORMATION (CONTINUED) Nup = 4.36 (8.53) Laminar, fully developed, uniform q; Summary of empirical correlations for the average Nusselt number for natural convection over surfaces: NUD = 3.66 (8.55) Laminar, fully developed, uniform T Geometry Characteristic Range of Ra Nu Length 8 Nup = 3.66 + -:0668 GZD (8.57) Laminar, thermal entry (or combined entry with 10'-10 1 + 0.04 Gzg Pr z 5), uniform T,, Gzo = (D/x) Rep Pr Vertical Plate Nu =0.59Ra 109-101 Nu =0.1Ra/3 3.66 Nu - tanh[2.264 Gz 13 + 1.7 Gzo23) + 0.0499 Gz tanh(Gz') (8.58) Laminar, combined entry, Pr 2 0.1, uniform T, GZD = (Dix) Rep Pr Nu = 0.825 + 0.387 Ray tanh (2.432 Pr(6 Gzp/6 ) Entire range 1+ (0.492 /Pr)46 27 V7= - 20 108 97 + 2:51 (8.20) Turbulent, fully developed Inclined Plate Use vertical plate equations as a first degree of approximation. f = (0.790 In Rep - 1.64) (8.21) Turbulent, fully developed, smooth walls, 3000 S Ren $ 5 X 10 Replace "g" by "g.cos(0)" for Ra 10,000, (LID) 210, n = 0.4 for T, > Tm Horizontal Plate and n = 0.3 for T,