Need exercise 2

c++

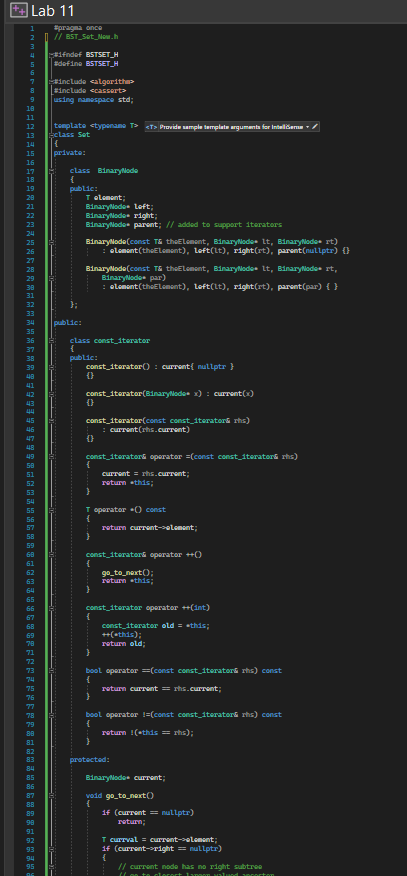
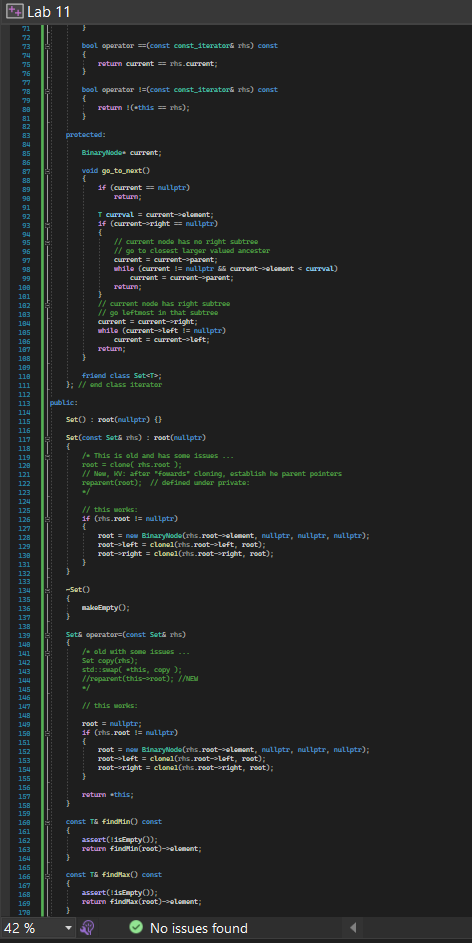
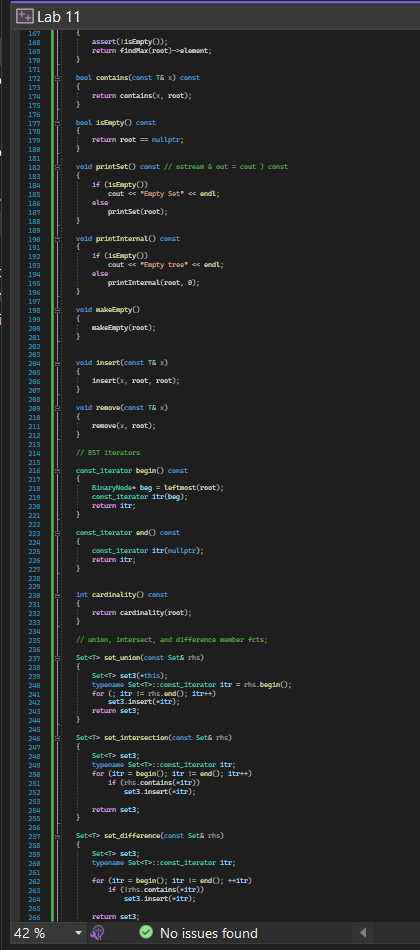
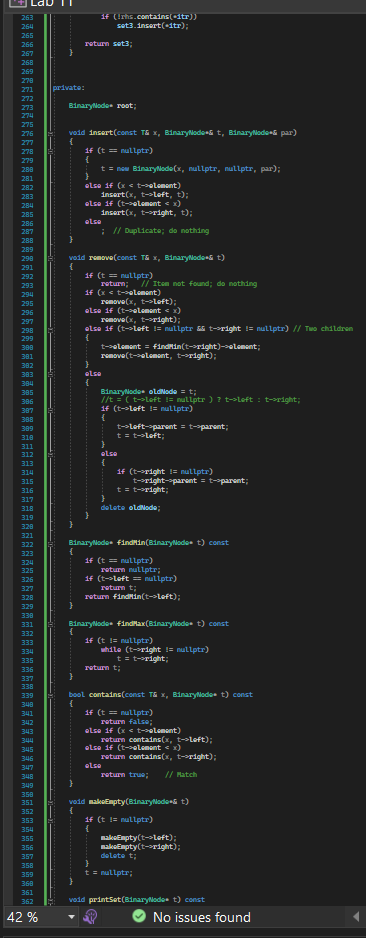
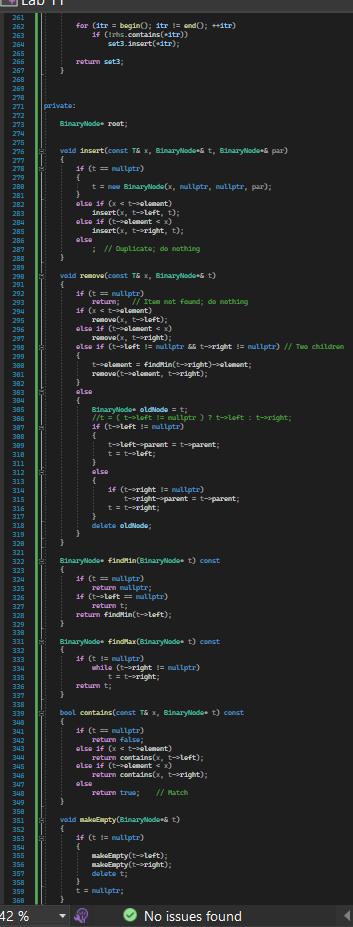
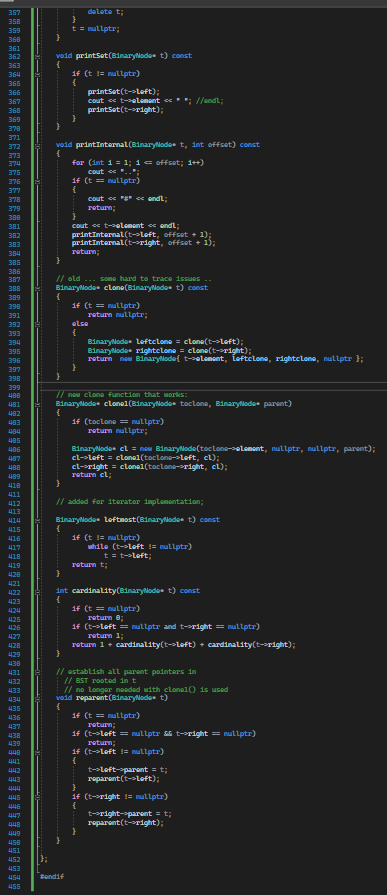
Exercise1a: Given header file BST_Set.h, write a new header file Set_Funtions.h and add to it a standalone (i.e., non-member function of class Set) functions that computes the union of two Sets. The set union function is to be a template function with header template typenane T ? Set set_union(const SetT)\& set1, const SetcT>\& set2) \{ // code to produce set that is union of set1 and set2, which // is the set of all elements in set1 or set2; 1/ // return the union set \} You will want to use Set::const_iterator to iterate over set1 and/or set2 for the purpose of computing the union. Exercise 1b: Add to file Set_Functions.h a function that computes the intersection of two Sets. The function header is: template typenane T> \{ // code to produce set that is intersection of set1 and set2, which // is the set of all elements that are in set1 AND set2; //- // return the intersection set \} Exercise 1c: Add to file Set_Functions.h a function that computes the set difference between two Sets. The function header is: terplate typenane To SetcTy set_difference(const SeteT>\& set1, const SeteT>\& set2) \{ /f code to produce set that is intersection of set1 and set 2 , which // is the set of all elements that are in set1 AND set2; // // return the set difference set \} Exercise 2: Write your own file SetMain.cpp with an int main() function that tests the three functions from 1ac. Implement an int main() that (1) generate and print out two sets of random numbers of size 10; (2) computes the union and intersection of both sets, and the two set-differences than be computed from both sets (e.g., A-B and B-A). (3) The program is to print out the resulting sets after each set operation. Sets can be printed with the printSet() member function of class Set T> Lab 11 Lab 11 bool operator I=(const const_1terators rhs) const \{ retum 1( this = rhs); protected: B1naryllado current; void go_to_next O 16 (cument = nutlptr) return: T currot = current-selenent; 1f ff current nade has no right nubtree /f go to closest larger va current = current-sparent: chile (current I= nutlots go f rotirm; // current node has rigit subtre the current = current-sight; white (current-steft I= nuttptr) return: friend class seteT?; b; setO)=root( mutLptr) \{\} set( const 5et=1 ths )=root( nut 1ptr) / this 15 otd and has sane 15sues. reparent(root); // defined under private: /f th1s works: 1f (rhs-root I = nultptr) 14 root = now B1narywado(rhs.reot-selenent, nuLLptr, nutLptr, nuLLptr); root-sleft = clanel(rhs_reot-sleft, reot); \{ makenptyO; 3 /o atd with se stad samap ( othis //reparent(th1s-soot); // way // this works: root = nutLptr; 1f (rhs_root I = nutlptr) root = now B1narylbdo(rths_root-selenent, nutLptr, nutlptr, nutlptr); root-sleft = clonel( rhs_root-sleft, root); ( return *this? b const TL findind A ( const assemt (110Enpty()) 3 const ta findtax (]) const. assert (11s Enpty O); retum f1ndhax(root)-elenent 42% - No issues found Exercise1a: Given header file BST_Set.h, write a new header file Set_Funtions.h and add to it a standalone (i.e., non-member function of class Set) functions that computes the union of two Sets. The set union function is to be a template function with header template typenane T ? Set set_union(const SetT)\& set1, const SetcT>\& set2) \{ // code to produce set that is union of set1 and set2, which // is the set of all elements in set1 or set2; 1/ // return the union set \} You will want to use Set::const_iterator to iterate over set1 and/or set2 for the purpose of computing the union. Exercise 1b: Add to file Set_Functions.h a function that computes the intersection of two Sets. The function header is: template typenane T> \{ // code to produce set that is intersection of set1 and set2, which // is the set of all elements that are in set1 AND set2; //- // return the intersection set \} Exercise 1c: Add to file Set_Functions.h a function that computes the set difference between two Sets. The function header is: terplate typenane To SetcTy set_difference(const SeteT>\& set1, const SeteT>\& set2) \{ /f code to produce set that is intersection of set1 and set 2 , which // is the set of all elements that are in set1 AND set2; // // return the set difference set \} Exercise 2: Write your own file SetMain.cpp with an int main() function that tests the three functions from 1ac. Implement an int main() that (1) generate and print out two sets of random numbers of size 10; (2) computes the union and intersection of both sets, and the two set-differences than be computed from both sets (e.g., A-B and B-A). (3) The program is to print out the resulting sets after each set operation. Sets can be printed with the printSet() member function of class Set T> Lab 11 Lab 11 bool operator I=(const const_1terators rhs) const \{ retum 1( this = rhs); protected: B1naryllado current; void go_to_next O 16 (cument = nutlptr) return: T currot = current-selenent; 1f ff current nade has no right nubtree /f go to closest larger va current = current-sparent: chile (current I= nutlots go f rotirm; // current node has rigit subtre the current = current-sight; white (current-steft I= nuttptr) return: friend class seteT?; b; setO)=root( mutLptr) \{\} set( const 5et=1 ths )=root( nut 1ptr) / this 15 otd and has sane 15sues. reparent(root); // defined under private: /f th1s works: 1f (rhs-root I = nultptr) 14 root = now B1narywado(rhs.reot-selenent, nuLLptr, nutLptr, nuLLptr); root-sleft = clanel(rhs_reot-sleft, reot); \{ makenptyO; 3 /o atd with se stad samap ( othis //reparent(th1s-soot); // way // this works: root = nutLptr; 1f (rhs_root I = nutlptr) root = now B1narylbdo(rths_root-selenent, nutLptr, nutlptr, nutlptr); root-sleft = clonel( rhs_root-sleft, root); ( return *this? b const TL findind A ( const assemt (110Enpty()) 3 const ta findtax (]) const. assert (11s Enpty O); retum f1ndhax(root)-elenent 42% - No issues found