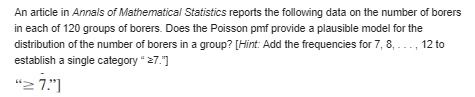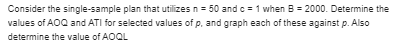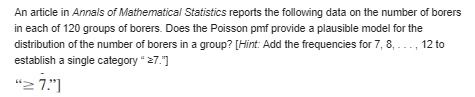
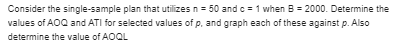
Need help:--

\fCriminologists have long debated whether there is a relationship between weather conditions and the incidence of violent crime. The author of the article "Is There a Season for Homicide?" (Criminology, 1988: 287-296) classified 1361 homicides according to season, resulting in the accompanying data. Test the null hypothesis of equal proportions using a = .01 by using the chi-squared table to say as much as possible about the P-value. 0 = .01An article in Annals of Mathematical Statistics reports the following data on the number of borers in each of 120 groups of borers. Does the Poisson pmf provide a plausible model for the distribution of the number of borers in a group? [Hint: Add the frequencies for 7, 8, . .., 12 to establish a single category " 27."] 7."]Each headlight on an automobile undergoing an annual vehicle inspection can be focused either too high (H), too low (L), or properly (N). Checking the two headlights simultaneously (and not distinguishing between left and right) results in the six possible outcomes HH, LL, NN, HL, HN, and L/. If the probabilities (population proportions) for the single headlight focus direction are P(H) = 01, P(L) = 62, and P(N) = 1 - 0, - 6, and the two headlights are focused independently of one another, the probabilities of the six outcomes for a randomly selected car are the following: P1 = 0; P2 = 02 P3 = (1 -01 - 02)2 PA = 20, 02 Ps = 20, (1 - 0, - #2) and the two Po = 202(1 - 0, - 02) Use the accompanying data to test the null hypothesis Hop, = TT, (0, , 02 ), . . . . Po = To (0,, 02) where the w,(0,, 0,)s are given previously. headlights are focused independently of one another, the probabilities of the six outcomes for a randomly selected car are the following: Outcome HH LL NN HL HN LN Frequency 49 26 14 20 53 38 [Hint: Write the likelihood as a function of 6, and &, take the natural log, then compute a/ad, and a/ad,, equate them to 0, and solve for #1, 02.] Use the accompanying data to test the null hypothesis Hop = #, (0,,02). . . .. P6 = T 6(0,, 02) where the + (0 , 0, )is are given previously. Outcome HH LL NN HL HN IN Frequency 49 26 14 20 53 38 [Hint: Write the likelihood as a function of 6, and 62, take the natural log, then compute a/20, and a/362, equate them to 0, and solve for . #2.]