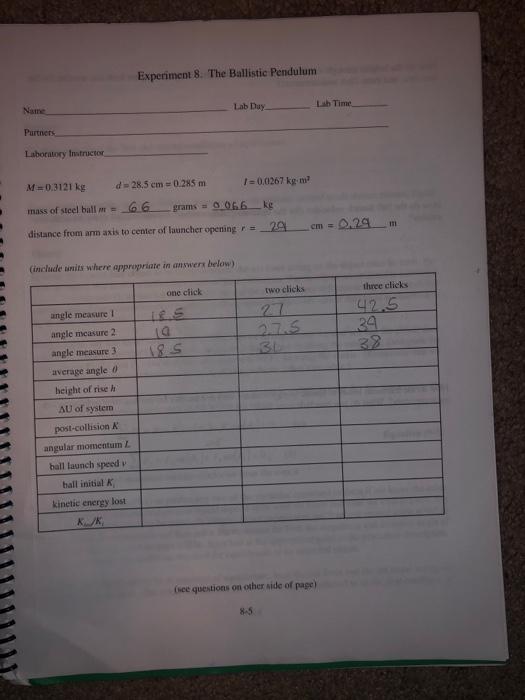
Purpose Experiment 8. The Ballistic Pendulum To examine a system applying ideas of conservation of both angular momentum and energy Apparatus Pasco ballistic pendulum, meter stick, pan balance Theory The ballistic pendulum consists of a spring-powered projectile launcher, a small steel hall, a ball catcher attached to a swinging arm, and an angular-measurement device to determine the angle through which the arm swings. In operation, the spring is initially compressed with the ball in front of the spring. When the spring is released from its initial position it gives the ball an initial velocity. Almost immediately after the ball exits the launcher it enters the catcher. The catching process is a completely inelastic collision We have previously considered inelastic collisions for straight-line motion. In this case, though, the on following the collision is a rotation about an axis. Thus, we apply the idea of conservation of angular momentum in our analysis of this system. Mechanical energy is lost during the collision but it is conserved in the motion following the collision As the arm swings with the ball and ball-catcher moving upward kinetic energy is transformed into gravitational potential energy. At the point of maximum rotation the energy is entirely potential and is equal to the kinetic energy immediately after the collision The next section provides the mathematical analysis for our system. The angular momentum of a "point-like" object is given by: Emvr. Equation (8-1) In Equation (8-1), m is the mass of the ball, vis its velocity as it leaves the launcher, und r is the distance between it (as it reaches the ball-catcher) and the axis of the arm. The angular momentum of an object with distributed mass in rotation about an axis is: L=10. Equation (8-2) Here, I is the moment of inertia (also known as rotational inertia) of the ball-catcher with the ball and the arm to which it is attached, and wo is its angular velocity. Immediately following the collision this value is the same as the angular momentum of the ball alone immediately prior to the collision. The kinetic energy of the rotating system is given by 8-1 .. T n Name Partners Laboratory Instructor d=28.5 cm=0.285 m angle measure I angle measure 2 angle measure 3 average angle height of rise h AU of system post-collision K Experiment 8. The Ballistic Pendulum M=0.3121 kg mass of steel ball - 66 grams 0066 kg distance from arm axis to center of launcher opening re (include units where appropriate in answers below) one click angular momentum L ball launch speed v ball initial K kinetic energy lost KJK Lab Day 19 18. S 1=0.0267 kg-m 29 two clicks 27 2.7.5 BL Lab Time cm = (see questions on other side of page) 0.29 m three clicks 42.5 34 38 How do the heights through which the system rises after the collision compare with one another for the one, two, and three-click measurements? How do the ball launch velocities (for the different "click-number" measurements) compare with one another? How do the fractional losses of kinetic energy compare with one another for the one, two, and three-click measurements? What do you conclude from this? 8-6 K = +10. The kinetic energy of the ball just prior to the collision was: K = {mv. Equation (8-4) We will use these two equations to determine the energy lost during the collision. Now, we need one more "building-block" equation. We need to know the gravitational potential energy of the system. Here, we start from our basic formula: U = Mgh, Equation (8-5) where M is the total system mass and his the height through which the system's center of mass rises. So, next, we need to determine that height from data that we'll acquire. The device we're using measures the angle from a vertical reference line. We'll call the distance from the axis to the center of mass d. We see that for any angle then the distance down from the axis height to that of the center of mass is d times the cosine of 8. When the collision occurs the center of mass is just a distance d straight down from the axis. So, the height through which the center of mass rises following the collision and prior to stopping is: h=d-(1-cos). Now, if we combine Equations (8-5) and (8-6) we obtain: U = Mgd-(1-cos). Equation (8-3) @ Equation (8-7) and the kinetic energy [expressed by Equation (8-3)) immediately after the collision must be (due to the conservation of mechanical energy) the same as this potential energy at the highest point. If we substitute this U from Equation (8-7) for the A in Equation (8-3) and solve for the angular velocity we find: 2K 2 Mgd-(1-cos) Equation (8-8) 1 If we next insert this result into Equation (8-2) we find. L = 2 Mgd1-(1-cose) Equation (8-6) Equation (8-9) for the angular momentum, both of the system immediately following the collision and for the ball alone immediately prior to the collision. L mir We now apply Equation (8-1) to find the speed of the ball prior to the collision. The ball's speed exiting the launcher was: Equation (8-10) For use in the equations above the following values are given: the mass Mf of the arm, catcher, and ball together is 0.3121 kg: and the distance d between the axis and the center of mass is 28.5 cm. The moment of inertia / of the system is 0.0267 kg-m.