Need help with all questions 1-6 for Discrete Mathematics. Question 6 has the option (1 through 5) for each drop down box. - Thank you

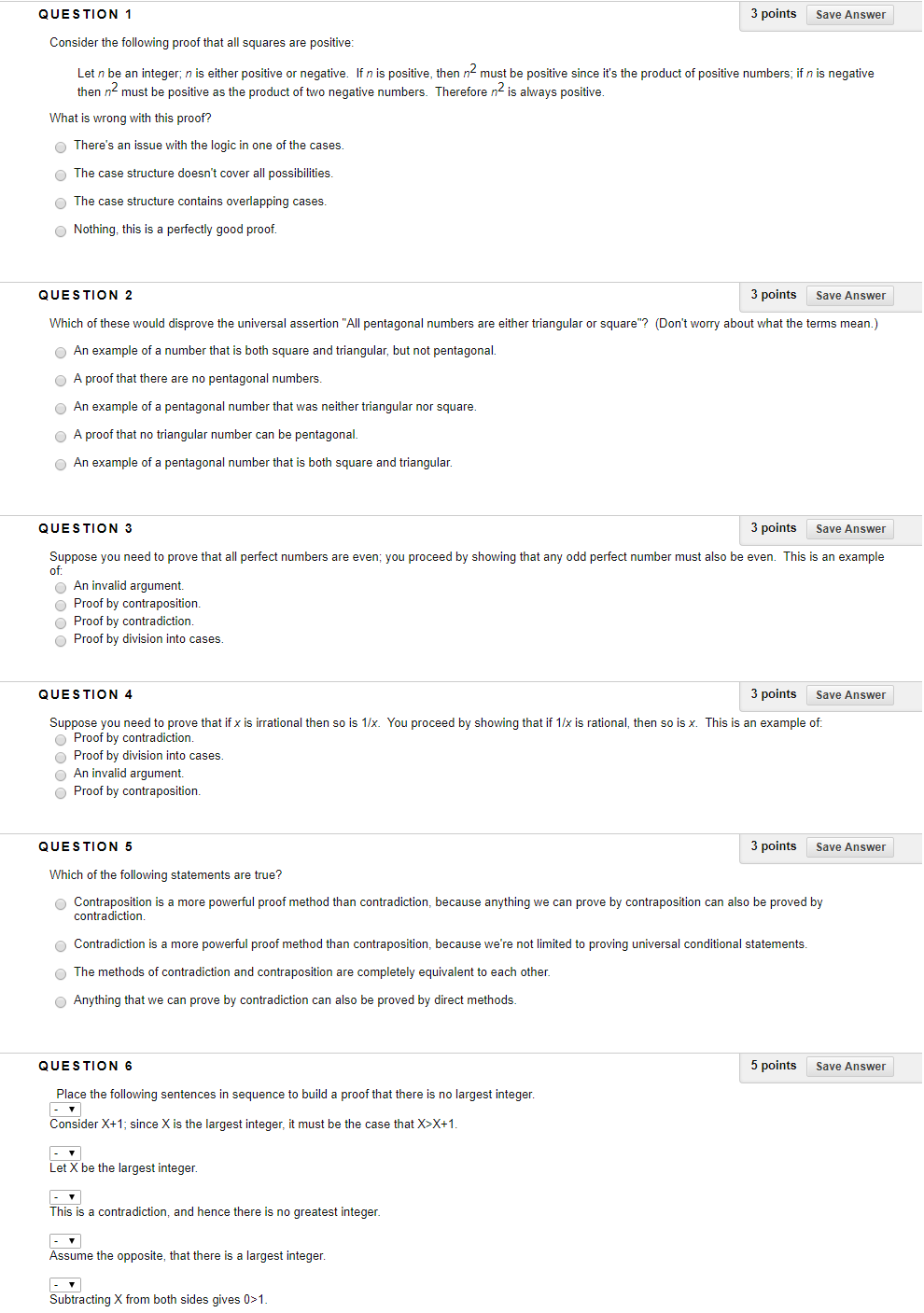
QUESTION 1 l 3poinls | SaveAnswer Consider the following proof that all squares are positive: Let n be an integer; n is either positive or negative. If r: is positive, then {/12 then n2 must be positive as the product of two negative numbers. Therefore n must be positive since it's the product of positive numbers; ifn is negative 2 is always positive. What is wrong with this proof? 0 There's an issue with the logic in one of the cases. 0 The case stmcture doesn't cover all possibilities. Q The case stmcture contains overlapping cases. 0 Nothing, this is a perfectly good proof. QUESTION 2 3poillts | SmAnswerl Which ofthese would disprove the universal assertion "All pentagonal numbers are either triangular or square"? [Don't worry abOutwhatthe terms mean.) 0 An example of a number that is both square and triangular, but not pentagonal. O A proof that there are no pentagonal numbers. 0 An example of a pentagonal number that was neither triangular nor square. 0 A proof that no triangular number can be pentagonal. 0 An example of a pentagonal number that is both square and triangular. QUESTION 3 3points |m Suppose you need to prove that all perfect numbers are even; you proceed by showing that any odd perfect number must also be even. This is an example of: 0 An invalid argument. 0 Proof by contraposition. 0 Proof by contradiction. 0 Proof by division into cases. QUESTION 4 3points | SmAnswerl Suppose you need to prove that ifx is inational then so is 1I'x. You proceed by showing that if 1!): is rational. then so is x. This is an example of: 0 Proof by contradiction. 0 Proof by division into cases. 0 An invalid argument. 0 Proof by contraposition. QUESTION 5 l 3points | SaveAnswer Which ofthe following statements are true? 0 Contraposition is a more powerful proof method than contradiction, because anything we can prove by contraposition can also be proved by contradiction. Q Contradiction is a more powerful proof method than contraposition, because we're not limited to proving universal conditional statements. 0 The methods of contra diction and contrapos'rtion are completely equivalent to each other. 0 Anything that we can prove by contradiction can also be proved by direct methods. QUESTION 6 I Spoints SmAnswer Place the following sentences in sequence to build a proof that there is no largest integer. El Consider )(+1; since X is the largest integer, it must be the case that x;x+1 _ El Let X be the largest integer. El his is a contradiction, and hence there is no greatest integer. El Assume the opposite, that there is 3 largest integer. El Su acting X from both sides gives UH. l