need help with c, d, and e please.
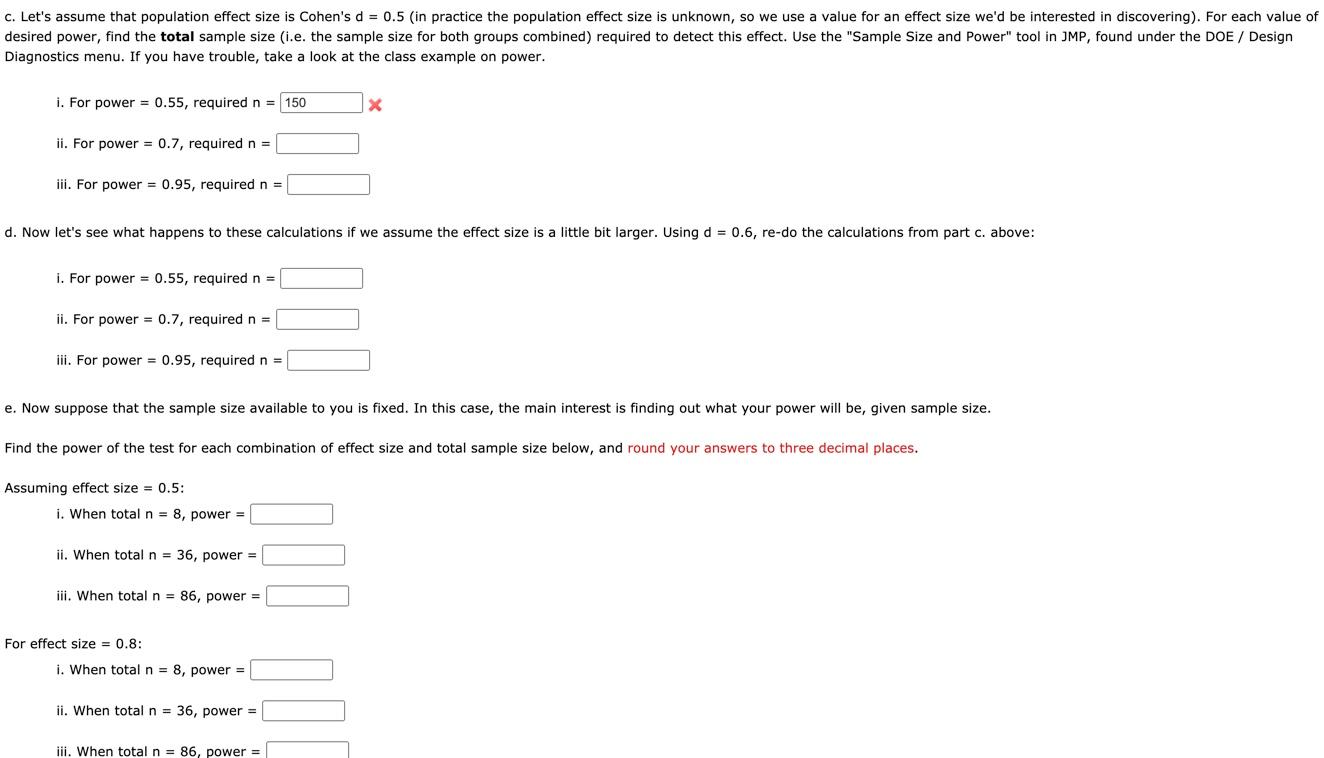
Suppose a study is being planned that will investigate whether female Beagles with severe periodontitis (gum and mouth disease) give birth to smaller litters of puppies, on average, than Beagles without periodontitis. Based on previous research, the standard deviation of litter size is estimated to be 2.6 puppies. Suppose we suspect that Beagles with periodontitis will give birth to on average 6 puppies whereas Beagles without periodontitis will give birth to on average 5 puppies. a. Using the assumed values above, calculate Cohen's d. d = 0.385 c. Let's assume that population effect size is Cohen's d = 0.5 (in practice the population effect size is unknown, so we use a value for an effect size we'd be interested in discovering). For each value of desired power, find the total sample size (i.e. the sample size for both groups combined) required to detect this effect. Use the "Sample Size and Power" tool in JMP, found under the DOE / Design Diagnostics menu. If you have trouble, take a look at the class example on power. i. For power = 0.55, required n = 150 x ii. For power = 0.7, required n = iii. For power = 0.95, required n = d. Now let's see what happens to these calculations if we assume the effect size is a little bit larger. Using d = 0.6, re-do the calculations from part c. above: i. For power = 0.55, required n = ii. For power = 0.7, required n = iii. For power = 0.95, required n = e. Now suppose that the sample size available to you is fixed. In this case, the main interest is finding out what your power will be given sample size. Find the power of the test for each combination of effect size and total sample size below, and round your answers to three decimal places. Assuming effect size = 0.5: i. When total n = 8, power = ii. When total n = 36, power = iii. When total n = 86, power = For effect size = 0.8: i. When total n = 8, power = ii. When total n = 36, power = iii. When total n = 86, power = Suppose a study is being planned that will investigate whether female Beagles with severe periodontitis (gum and mouth disease) give birth to smaller litters of puppies, on average, than Beagles without periodontitis. Based on previous research, the standard deviation of litter size is estimated to be 2.6 puppies. Suppose we suspect that Beagles with periodontitis will give birth to on average 6 puppies whereas Beagles without periodontitis will give birth to on average 5 puppies. a. Using the assumed values above, calculate Cohen's d. d = 0.385 c. Let's assume that population effect size is Cohen's d = 0.5 (in practice the population effect size is unknown, so we use a value for an effect size we'd be interested in discovering). For each value of desired power, find the total sample size (i.e. the sample size for both groups combined) required to detect this effect. Use the "Sample Size and Power" tool in JMP, found under the DOE / Design Diagnostics menu. If you have trouble, take a look at the class example on power. i. For power = 0.55, required n = 150 x ii. For power = 0.7, required n = iii. For power = 0.95, required n = d. Now let's see what happens to these calculations if we assume the effect size is a little bit larger. Using d = 0.6, re-do the calculations from part c. above: i. For power = 0.55, required n = ii. For power = 0.7, required n = iii. For power = 0.95, required n = e. Now suppose that the sample size available to you is fixed. In this case, the main interest is finding out what your power will be given sample size. Find the power of the test for each combination of effect size and total sample size below, and round your answers to three decimal places. Assuming effect size = 0.5: i. When total n = 8, power = ii. When total n = 36, power = iii. When total n = 86, power = For effect size = 0.8: i. When total n = 8, power = ii. When total n = 36, power = iii. When total n = 86, power =
