Need Help with Computational Physics HW for python on calculating electrostatic potential.

Book from Computational physics by mark newman

Need it solved in Overrelaxation method:

Exercise 9.3:

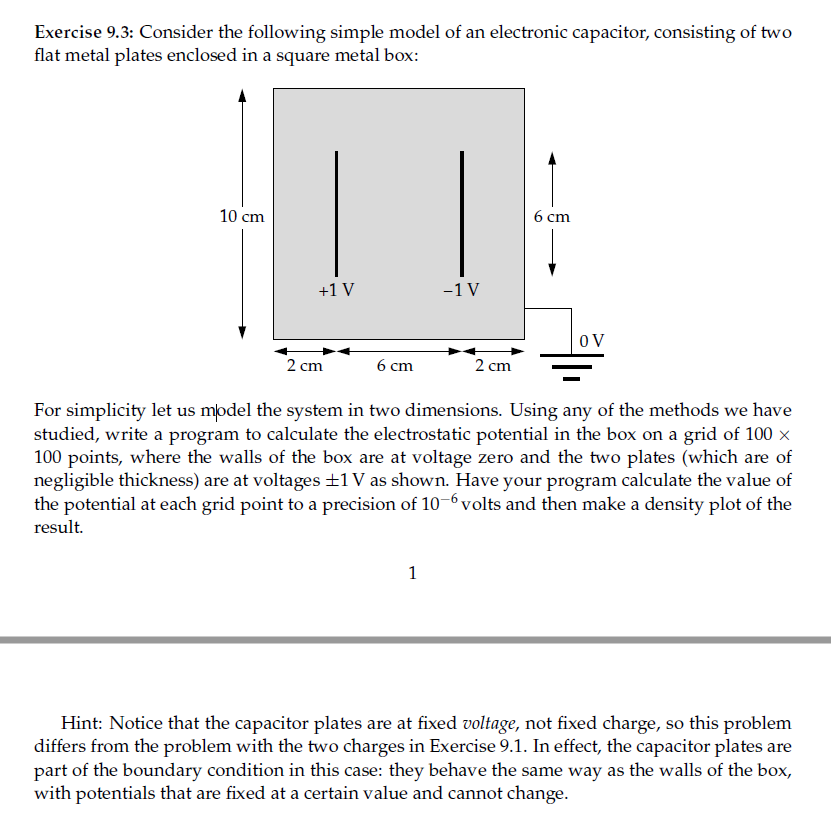
V 0 volts Figure 9.1: A simple electrostatics problem. An empty box has conducting walls, all of which are grounded at 0 volts except for the wall at the top, which is at some other voltage V. The small gaps between the top wall and the others are intended to show that they are insulated from one another. We'll assume in our calculations that these gaps have negligible width. the equation takes the form 2x2 + 7 =0. (9.2) The challenge is to solve this equation inside the box, subject to the boundary conditions that o = V on the top wall and $ = 0 on the other walls. The other broad class of partial differential equation problems are the ini- tial value problems. In an initial value problem, the field or other variable of interest is not only subject to boundary conditions, but is also time varying. Typically we are given the initial state of the field at some time f = 0, in a manner similar to the initial conditions we used for ordinary differential equa- tions in Chapter 8, and we want to calculate how the field evolves over time thereafter, subject to that initial condition plus the boundary conditions. An example of an initial value problem would be the wave equation for the vi- bration of a string, like a string in a musical instrument, for which there are boundary conditions (the string is usually pinned and stationary at its ends) but also an initial condition (the string is plucked or struck at t = 0) and the challenge is to solve for the motion of the string.9.2.1 UVERRELAXATIDN On each iteration of the Jacobi method the values of #3 on all the grid points converge a little closer to their nal values. Cine way,r to make this convergence faster is on each step to \"overshoot" the new value a little. For instance, sup- pose on a particular grid point the value goes from [1.1 to 13 on one iteration. and eventually converges to I15 it we wait long enough. Then we could ob- serve those values 111 and 0.3 and tell ourselves, Ir'Instead of changing to ill\": on this step, let's overshoot and go to, say, [14." in this case, doing so will get us closer to the nal value of 0.5. This method is called evorslexalierr. In detail it works like this.l Consider again the solution of [aplaee's equation, as in Example 9.1. and suppose at some point in the operation of our program we have a set ot val- ues 1H1, 5*} on our grid points and at the next iteration we have a new set $11, 3;) "if you did Exercise 6.11 on page 2&0. then you have seen the basic idea behind overtelaxa lion before, albeit in the content of ordinary algebraic equations rather than diferential equations. calculated from Eq. (9.9). Then the new set can be written in terms of the old as $'(x, y) = $(x,y) + Ap(x, y), (9.13) where Ap(x, y) is the change in o on this step, given by Ap(x, y) = $'(x, y) - (x, y). Now we define a set of overrelaxed values ow (x, y) by Pw(x, y) = $(x, y) + (1+w)Ap(x,y), (9.14) where w > 0. In other words we change each p(x, y) by a little more than we normally would, the exact amount being controlled by the parameter w. Substituting Ap(x,y) = $'(x,y) - $(x, y) into Eq. (9.14) gives Pw (x, y) = $(x,y) + (1+ w)[p'(x,y) -$(x,y)] = (1 + w)p' (x, y) - wp(x,y) 1 + w p( x ta,y) + p(x - a,y) + $(x, y + a) + p(x,y - a)] -wp(x,y). (9.15) where we have used Eq. (9.9) for p'(x, y). The overrelaxation method involves using this equation instead of Eq. (9.9) to calculate new values of o on each step, but in other respects is the same as the Jacobi method. In order to use the equation we must choose a value for the parameter w. We discuss in a moment how this is done.in the following sections of this chapter we will look at techniques for solv ing both boundary value problems and initial value problems. 9.1 BOUNDARY 1It-".tLl.fE PROBLEMS AND THE RELAXATION METHOD A fundamental technique for the solution of partial differential equations is the method ofnits dierenccs. Consider the electrostatics example of Fig. 9.1, whose solution invoives solving laplace's equation, Eq. {9.2), for the electric potential it, subject to the appropriate boundary' conditions. To make the pic- tures manageable [and the programs easier} let's consider the problem in two- dimensional space, where Laplace's equation takes the simpler form a+#-=n. {as} Real problems are in three dimensions. of course, but the techniques for two and three dimensions are fundamentally the same; once we can do the two- dimensional version, the threedimensional one is a straightforward general- ization. The method of nite differences involves dividing space into a grid of dis- crete points. Man},r kinds of grids are used, depending on the particular prob- lem in hand, but in the simplest and commonest case we use a regular, square grid as shown in Fig. 9.2. Note that we put points on the boundaries of the space [where we already know the value of (p) as well as in the interior {where we want to calculate the solution]. Suppose the spacing of the grid points is a and consider a point at position {1, 3'}. As we saw in Section 5.10.5, second derivatives can be approximated using a nite difference formula, just as rst derivatives can, and, as we saw in Section 5.1115, so can partial derivatives. Applying the results we learned in those sections {particularhr Eq. [5.109] on page 1'97], we can write the second derivative of qt: in the x-direction as 3250 = W [a 4} 312 n2 ' i This formula gives us an expression for the second derivative in terms of the vaiues satiny}, {pile a, y}, and :pIEJc + a, y} at three adjacent points on our grid. Similarly the derivative in the ywdirection is 32$ _ vireo} +vtrnit -} - litter} 3? n,. [9.5: words, we have turned our problem from the solution of a partial differential equation into the solution of a set of linear simultaneous equations. We studied the solution of simultaneous equations in Chapter ti, where we saw that sets of equations like [93} can be solved by a variety of methods. such as Gaussian elimination {Section 5.1.1} or LU decomposition {Section 5.1.4]. In the present case, however, because the equations are particularly simple, there is a quicker way to solve them: we can use the relaxation method of Section 6.3.]. We introduced the relaxation method as a method for the solu- tion of nonlinear equations, but there's no reason in principle why it cannot be applied to linear ones as well, and in the preeem case it's actually a good choicebetter than Gaussian elimination, for instance. because it involves less work, both for the programmer and for the computer. To make use of the relaxation method, we rearrange Eq. {93"} to read vinyl = live + as} + so i as) + May + a} + visit will. (9.3} which tells us that Mr, 3;} is simply the average of the values on the immedi ately adjacent points of the grid. Now we fix plx, y} at the boundaries of the system to have the value that we know it must have, which for the current electrostatic problem means (p = if on the top wall of the box and d3 .-_- D on the other three walls. Then we guess some initial values for :qux, y} at the grid points in the interior of the box. The guesses don't have to be good ones. For instance, we could just guess that the values are all zero, which is obviously wrong, but it doesn't much matter. Now we apply Eq. {9.8} to calculate new values :p' on all the grid points in the interior space. That is, we calculate my: = the + w) + an vry1+ are + n} + eta it ~ a1]. {9.9} Then we take these values and feed them back in on the righthand side again to calculate another new set of values. and so on until p settles down to a fixed value. if it does that means that we have found a solution to Eq. (9.3]. This approach for solving the Laplace equation is called the Jacobi method. Like all relaxation methods. it does require that the iteration process actually converge to a solution, rather than diverging; as we saw in Section 6.3.1, this is not always guaranteed for relaxation methods. Situations where the calcula- tion diverges are said to be numerically unstable, and there are some relaxation methods for partial differential equations that can be numerically unstable. But it toms out that the Jacobi method is not one of them. It can be proved that the Jacobi method is always stable and so always gives a solution. As described in Section 6.3.1, there are a couple of different ways to decide when to stop the iteration process for the relaxation method, of which the sim- plest is just to wait until the values of $ stop changing, at least within whatever limits of accuracy you have set for yourself. Thus, having calculated ' (x,y) from Eq. (9.9), you could calculate the change p'(x, y) - (x, y) and when the magnitude of this change is smaller than your target accuracy on every grid point, the calculation ends. EXAMPLE 9.1: SOLUTION OF LAPLACE'S EQUATION Let us compute a solution to the two-dimensional electrostatics problem of Fig. 9.1 using the Jacobi method, for the case where the box is I'm along each side, V = 1 volt, and the grid spacing a = 1 cm, so that there are 100 grid points on a side, or 101 if we count the points at both the beginning and the end. Here's a program to calculate the solution and make a density plot of the result: from numpy import empty, zeros, max File: laplace . py from pylab import imshow, gray, show # Constants M = 100 # Grid squares on a side V = 1.0 # Voltage at top wall target = 1e-6 # Target accuracy # Create arrays to hold potential values, phi = zeros ( [M+1 , M+1] , float) phi [o, : ] = V phiprime = empty ( [M+1 , M+1] , float) # Main loop delta = 1.0 while delta>target: # Calculate new values of the potential for i in range (M+1) : for j in range (M+1) : if i==0 or i==M or j==0 or j==M: phiprime [i, j] = phi[i, j] else: phiprime [i, j] = (phi [i+1, j] + phi[i-1, j] \\ + phi [i, j+1] + phi[i, j-1])/4 40ti Calculate maximum ditterauce from old values delta = uaatabstphi-phipriuall # Strap the too arrays around phi,phipr1ma = phiprima .phi it Make a plot tusbovtplii) grayfl sheet) A couple of things are worth noting in this program. First, observe that nei~ ther the system size L nor the grid spacing If ever enters into the calculation. We perform the whole calculaon in terms of the indices 1 and j of the grid points. integers that run from I] to' l and whiCh we can conveniently use as the indices of the arrays phi and phiprime that hold the values of the electric potential. Notice also how when we calculate the new values of p, which are stored in the array pbiprima, we run through each point :i . j and rst check whether it is on the boundary of the box. If it is, then the new value if of the electric potential is equal to the old one gitthe electric potential never changes on the boundaries. If, on the other hand, the point is in the interior of the box then we calculate a new value using Eq. {9.9). Finally, notice the line "phi,phiprime H phiprilrle..pl:ii\"J which swaps anmmd the two arrays phi and phiprime. so that the new values of electric potential get used as the old values the next time around the loop. Figure 9.3 shows the density plot that results from running the program. As we can see, there is a region of high electric potential around the top wall of the box, as we would expect, and low potential around the other three walls. It's important to appreciate that, since we have approximated our deriva ves with nite differences. theJacobi method is only going to give us an ap proximate solution to our problem. Even if we make the target accuracy for the iteration very small, the solution will still contain. relatively large errors be cause the nite difference approximation to the second derivative is not very accurate. One can use higher-order derivative approximations, of the kind we studied in Section 5.11.14, to improve the accuracy of the calculation-the generalization of the method is straightforwardor one can just increase the number of grid points, making them closer together. which improves the ac- curacy of the current approxirnation. Increasing the number of grid points, Figure 9.3: Solution of the laplace equation. A density plot of the electric potential for the two-dimensional electrostatics problem shown in Fig. 9.1, calculated using the Iacohi method. however, will also make the program run more slowly. Another point to notice is that the calculation gives us the value of at only at the grid points and not elsewhere. If we need values in between the grid points we could calculate them using an interpolation scheme such as the linear inter- polation of Section 5.11, although this introduces a further approximation. This approximation can also be improved by making the grid size smaller, though agin the resulting program will run more slowly. A more technical point to be aware of is that the boundaries around our space may not always be simple and square the way they are in the exercise above. We may have diagonal surfaces or round surfaces or holes cut out of the space. Such things can make it difcult to divide up the space with a square grid because the grid points don't fall exactly on the boundaries. We can at- ways approximate an inconvenient shape by moving the boundaries to the grid points closest to them, applying the boimdary conditions at these points rather than exactlyr on the true boundaries. This, however. introduces more approximations into the calculation. There exist more complicated nite dif- ference methods that get around these issues by using grids whose spacing CHAPTER. 9 PARTIAL DIFFERENTIAL EQUATIONS DME UP the most challenging problems in computational physicsand also some of the most interestinginvolve the solution of partial differential equations, such as the wave equation, the diffusion equation, the Laplace and Poisson equations, Maxwell's equations, and the Schrodinger equation. Al- though the basic numerical methods for solving these problems are straight- forward, they are also computationally demanding, so a lot of effort has been invested in nding ways to arrive at solutions quickly. As with the ordinary differential equations of Chapter 3, problems involv- ing partial differential equations can be divided into initial value problems and boundary value problems. By contrast with the situation in Chapter 8, how- ever, boundary value problems for partial differential equations are usually simpler to solve than initial value problems, so we'll study them rst. Wit boundary value problems we have a partial differential equation describing the behavior of a variable in a space and we are given some constraint on the variable around the boundary of the space. The goal is to solve for the values inside the rest of the spaoe. A classic example of a boundary value problem is the problem of solving for the electric potential in electrostatics. Suppose, for instance, we have a box as shown in Fig. 9.1. The box is empty and has one wall at voltage 'v' and the others at voltage zero. Our goal is to determine the value of the electrostatic potential at points within the box. Problems like this arise in electronics and in many physics experiments. The electrostatic potential if: is related to the vector electric field E by E = vs. And Maxwell's equations tell us that V - E -_ t} in the absence of any electric charges, so V . Val = [I or so = a, (9.1} which is Lsplece's equation. If we write out the Laplacian operator '31 in full, 431 Exercise 9.3: Consider the following simple model of an electronic capacitor, consisting of two at metal plates enclosed in a square metal box: 1 lcm 6cm +1'tir 1V T qpqHh 0V 2cm 6cm 2cm For simplicity let us m|odel the system in two dimensions. Using any of the methods we have studied, write a program to calculate the electrostatic potential in the box on a grid of 100 x 100 points, where the walls of the box are at voltage zero and the two plates [which are of negligible thickness) are at voltages :|:1 V as shown. Have your program calculate the value of the potential at each grid point to a precision of 106 volts and then make a density plot of the result. Hint: Notice that the capacitor plates are at xed voltage, not xed charge, so this problem differs from the problem with the two charges in Exercise 9.]. In effect, the capacitor plates are part of the boundary condition in this case: they behave the same way as the walls of the box, with potentials that are xed at a certain value and cannot change