Need help with problems 11-20. Answers only is fine if you want. I'll give helpful rating.

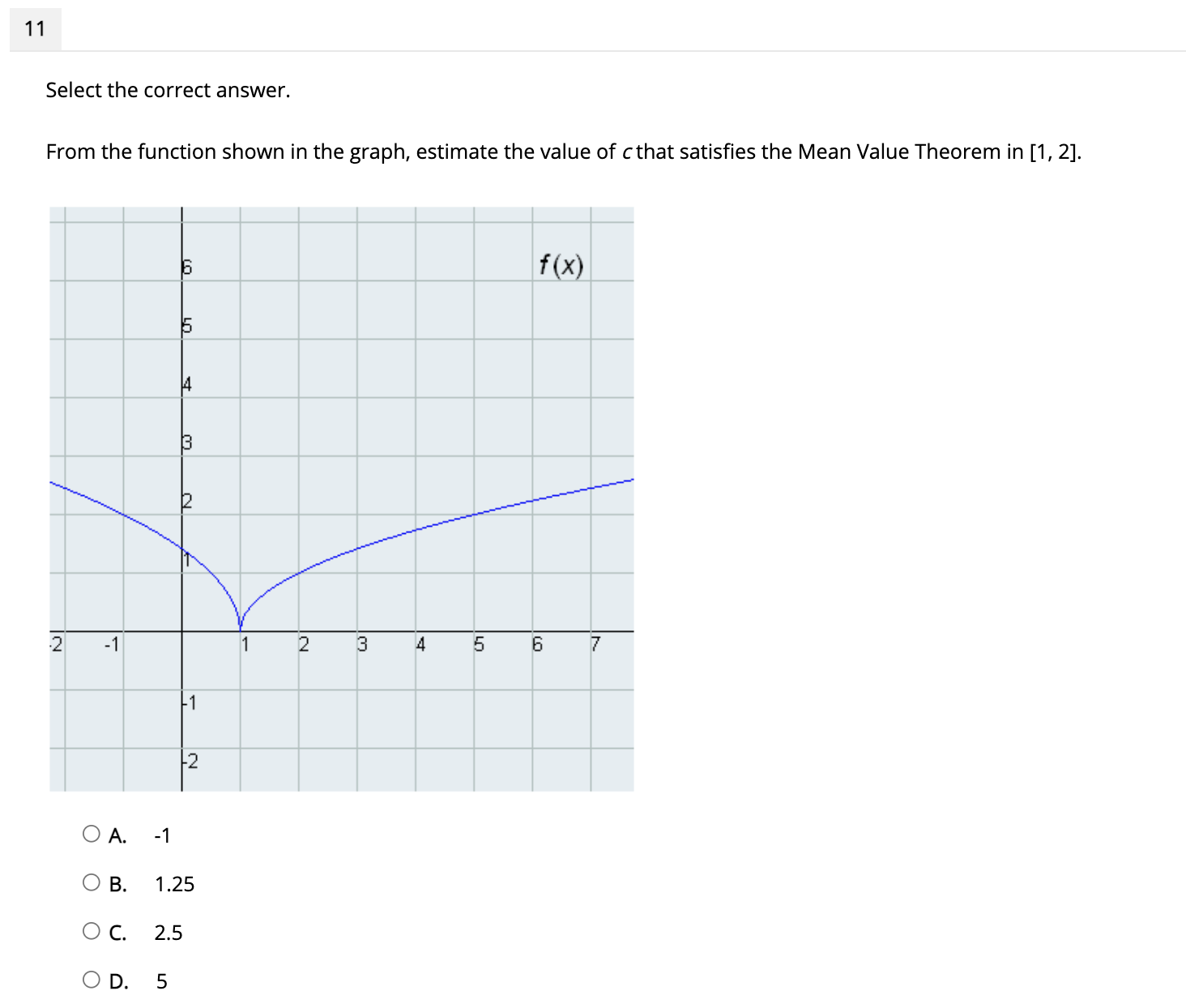
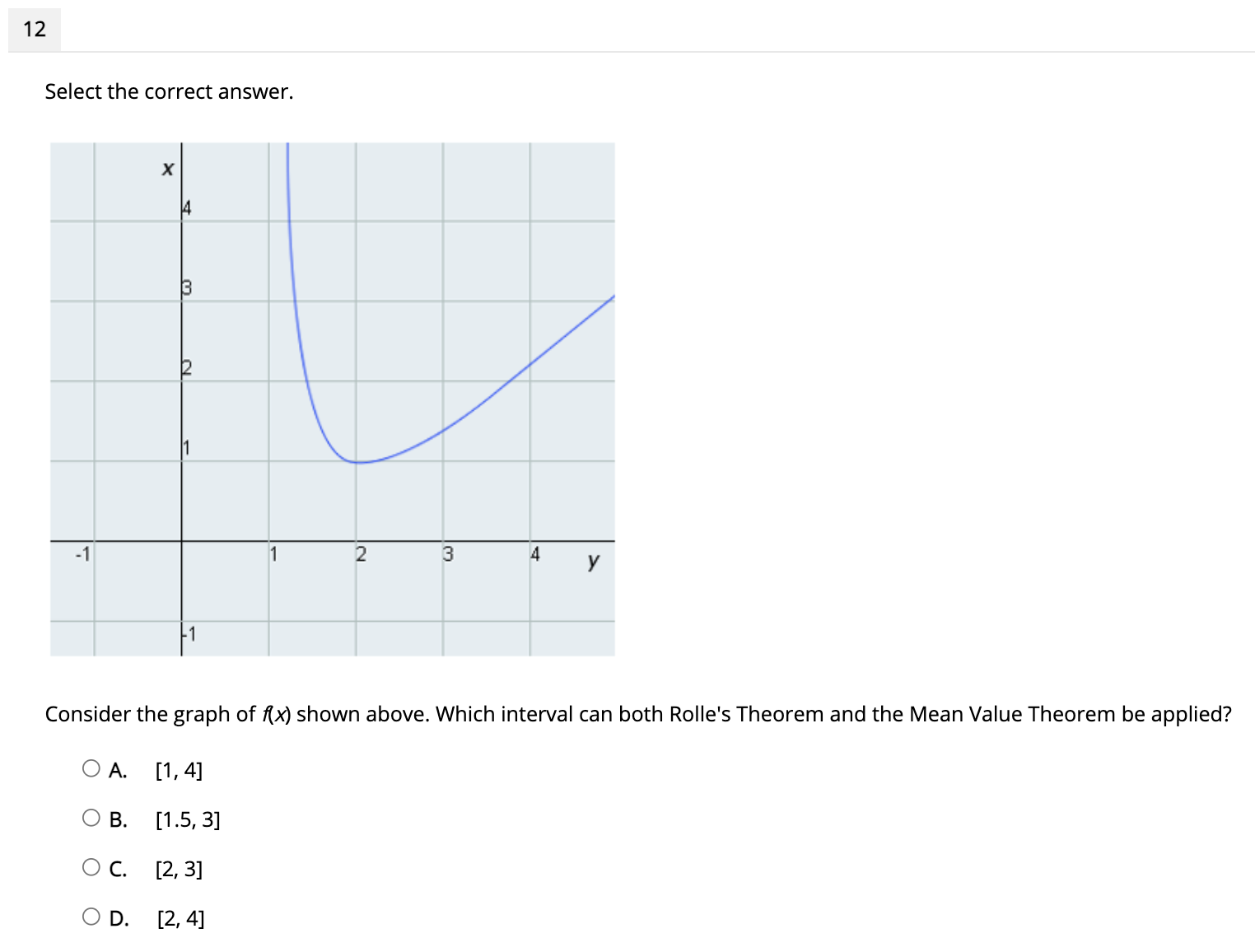
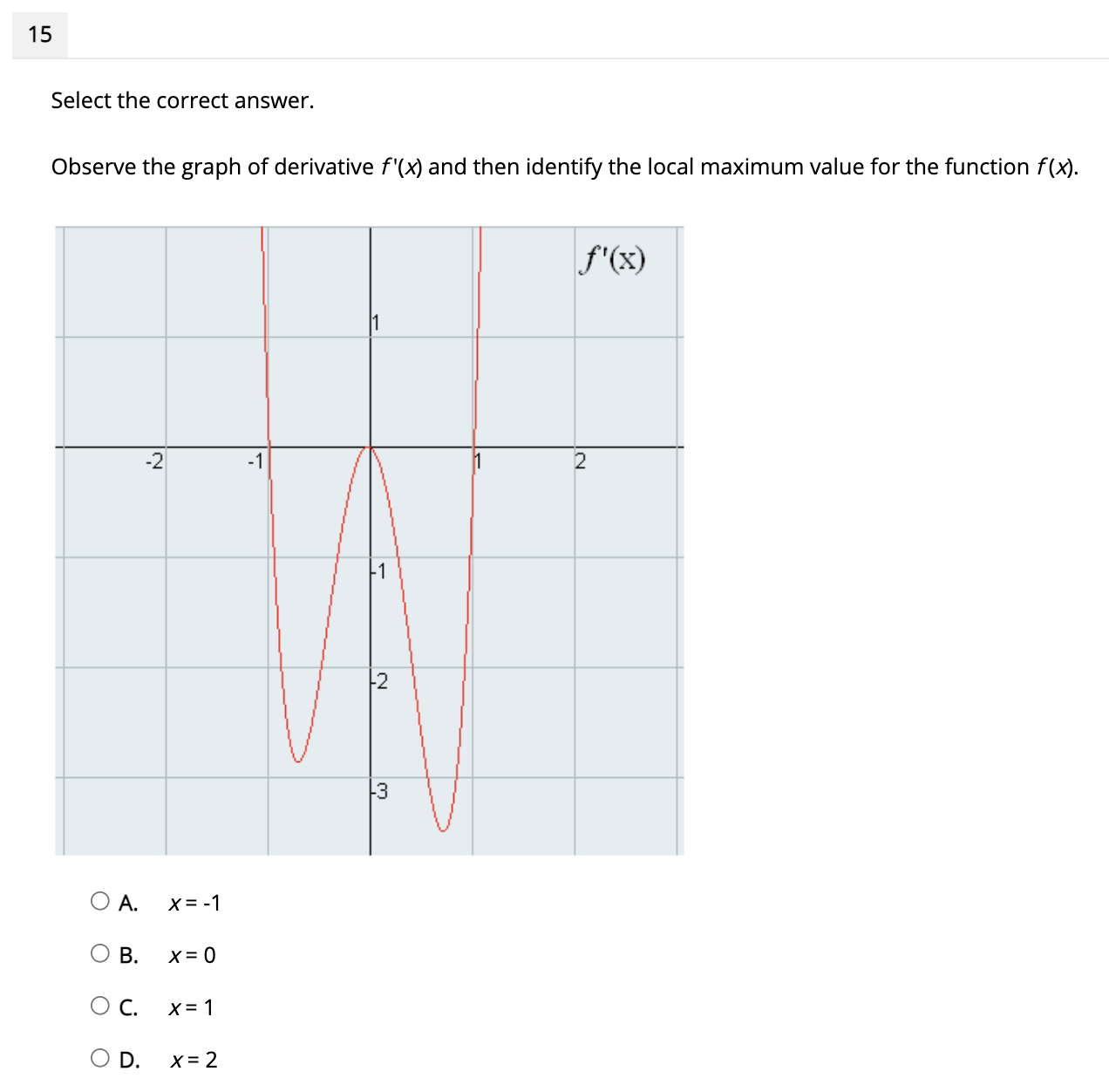
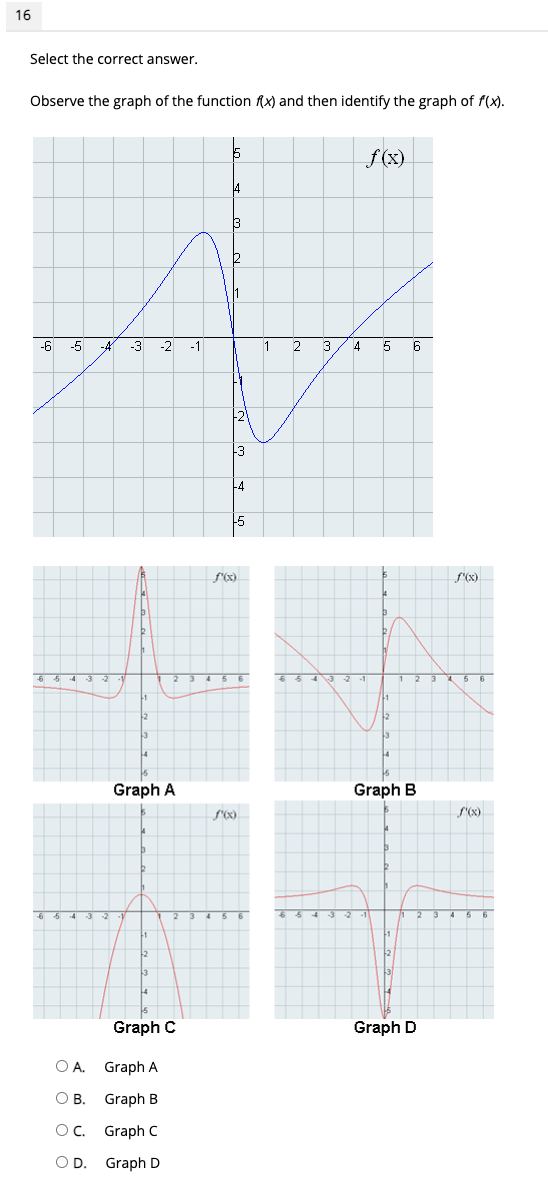
11 Select the correct answer. From the function shown in the graph, estimate the value of c that satisfies the Mean Value Theorem in [1, 2]. f (x) 5 14 3 2 -1 1 2 3 4 5 6 7 -1 2 O A. -1 O B. 1.25 O C. 2.5 OD. 512 Select the correct answer. X 14 -1 2 3 4 Consider the graph of f(x) shown above. Which interval can both Rolle's Theorem and the Mean Value Theorem be applied? O A. [1, 4] O B. [1.5, 3] O C. [2, 3] O D. [2, 4]13 Select the correct answer. 3 Identify the local minimum value for the function f(x) = x 2x2 + 5 , using the first derivative test. 0 A. X: -'l .4 O B. x= 0 O C. X: 2 OD. X4 14 Select the correct answer. X3 Given the function x) = _ _ Bx , nd the interval in which the function is decreasing? O A. (-ool -2:I O B. [-2. 2) O C. (2. on) O D. (-00. co) . Select the correct answer. Observe the graph of derivative f'(x) and then identify the local maximum value for the function for). 16 Select the correct answer. Observe the graph of the function f(x) and then identify the graph of f(x). UT f ( x) 4 2 7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 -2' 3 -4 -5 f'(x) f(x) 654 3 2 23 4 5 5 6 5 3 2 Graph A Graph B S'(x) f'(x) 654 32 2 3 4 5 6 6 5 4 3 2-1 2 Graph C Graph D O A. Graph A O B. Graph B O C. Graph C OD. Graph D18 Select the correct answer. When does f(x) = x - 3x2 + 10 have an inflection point? O A. x= 0 and x = 1/2 OB. x=-v2 and x = 1 OC. x=-2 and x = 12 OD. X = - NI - and X = /19 Select the correct answer. Which best describes the concavity of the function {(x) = x3 - 3 , in the interval (0, 5)? X 0 A. concave upward in the interval (0, 5) O B. concave upward in the interval (0.9, 5) O C. concave downward in the interval (0, 5) O D. concave upward in the interval (0.5, 2) 20 Select the correct answer. Apply the Second Derivative Test to identify the local minima for the function fix) = xi _ x? OA. X= 1 OB. X= WH OC. X= 0 OD. X = -. W / H17 Select the correct answer. Apply the Second Derivative Test to identify the local maxima for the function /(X) = - X OA. X= 0 O B. X= 1.14 OC. x= 2 OD. X= 3