Need help with screenshots one through 10 (1-10). All information needed to solve these problems can be found individually below, in each respective screenshot. The only thing you need to answer are the blanks in each screenshot, where numbers already lye highlighted by a mute blue, those are already answered. Each screenshot requires one answer from you. Thanks.

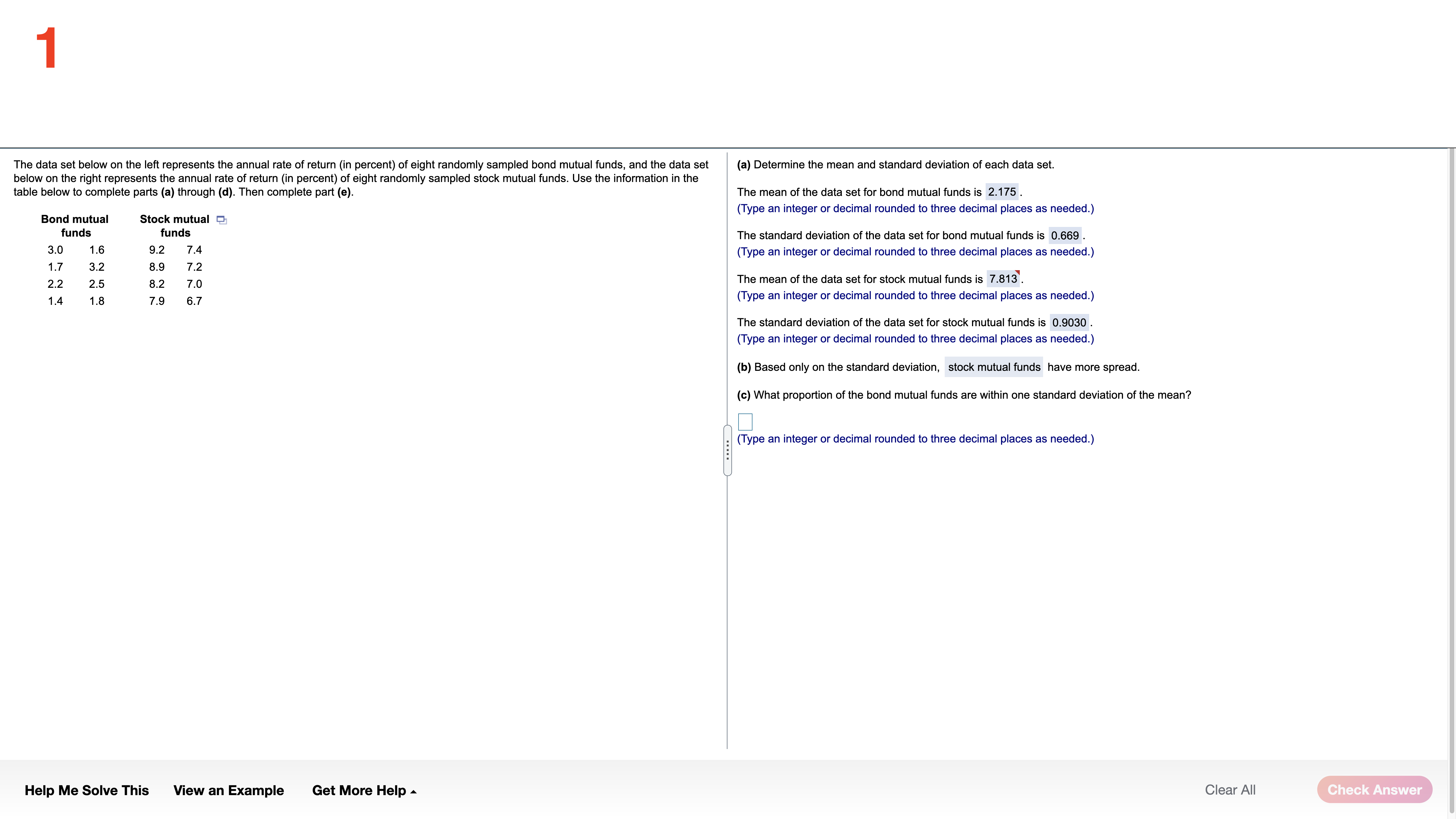
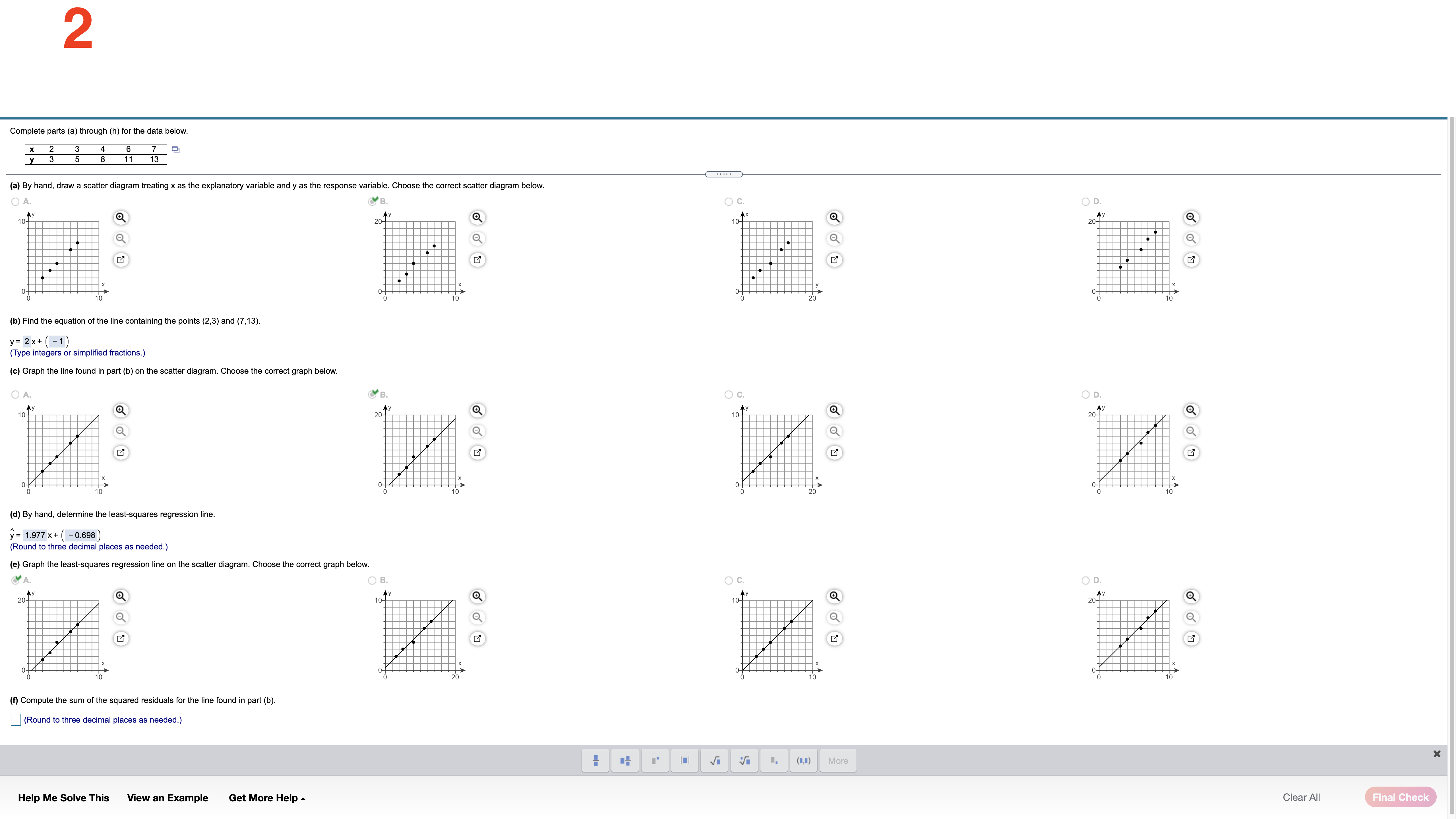
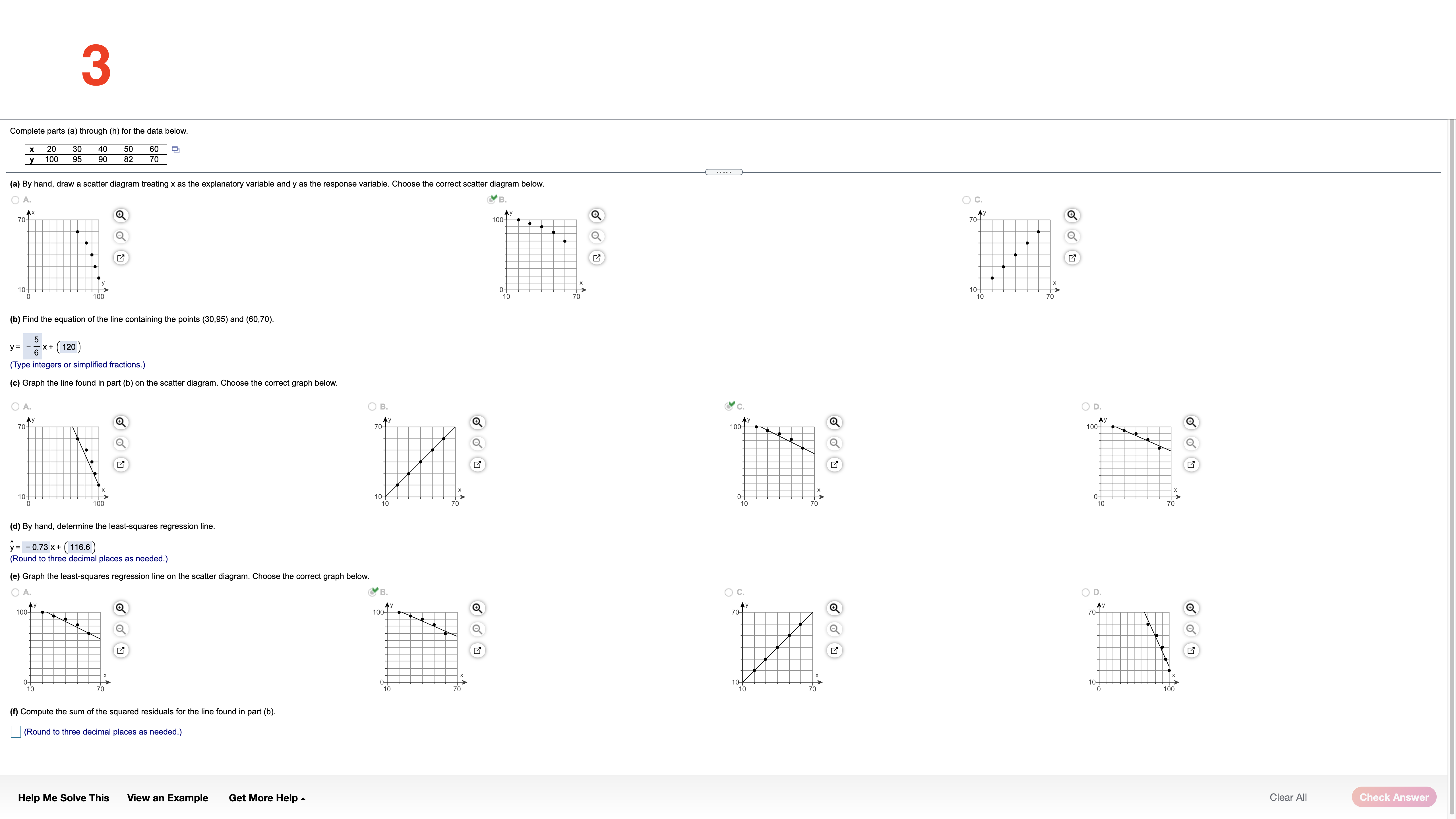
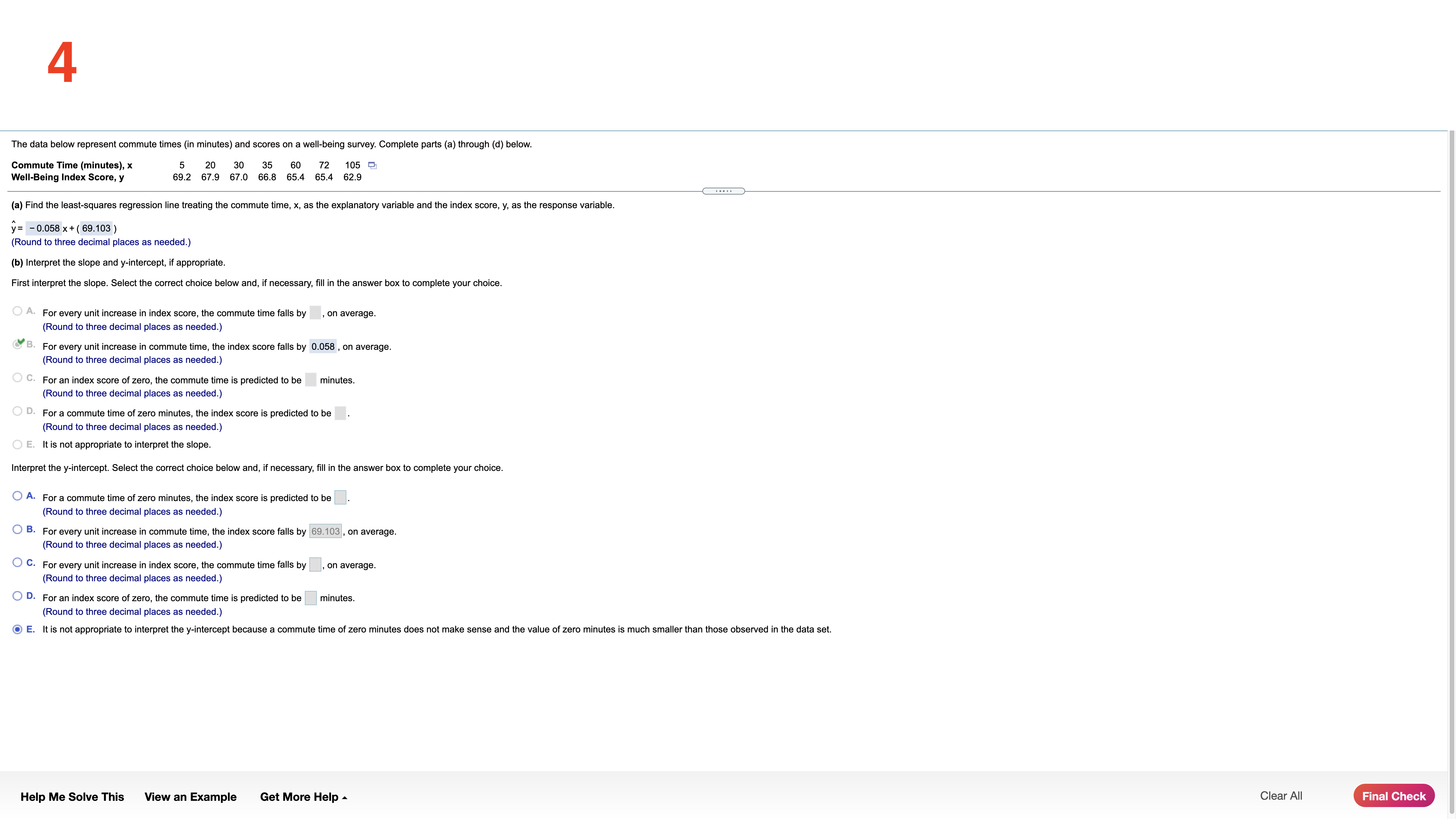
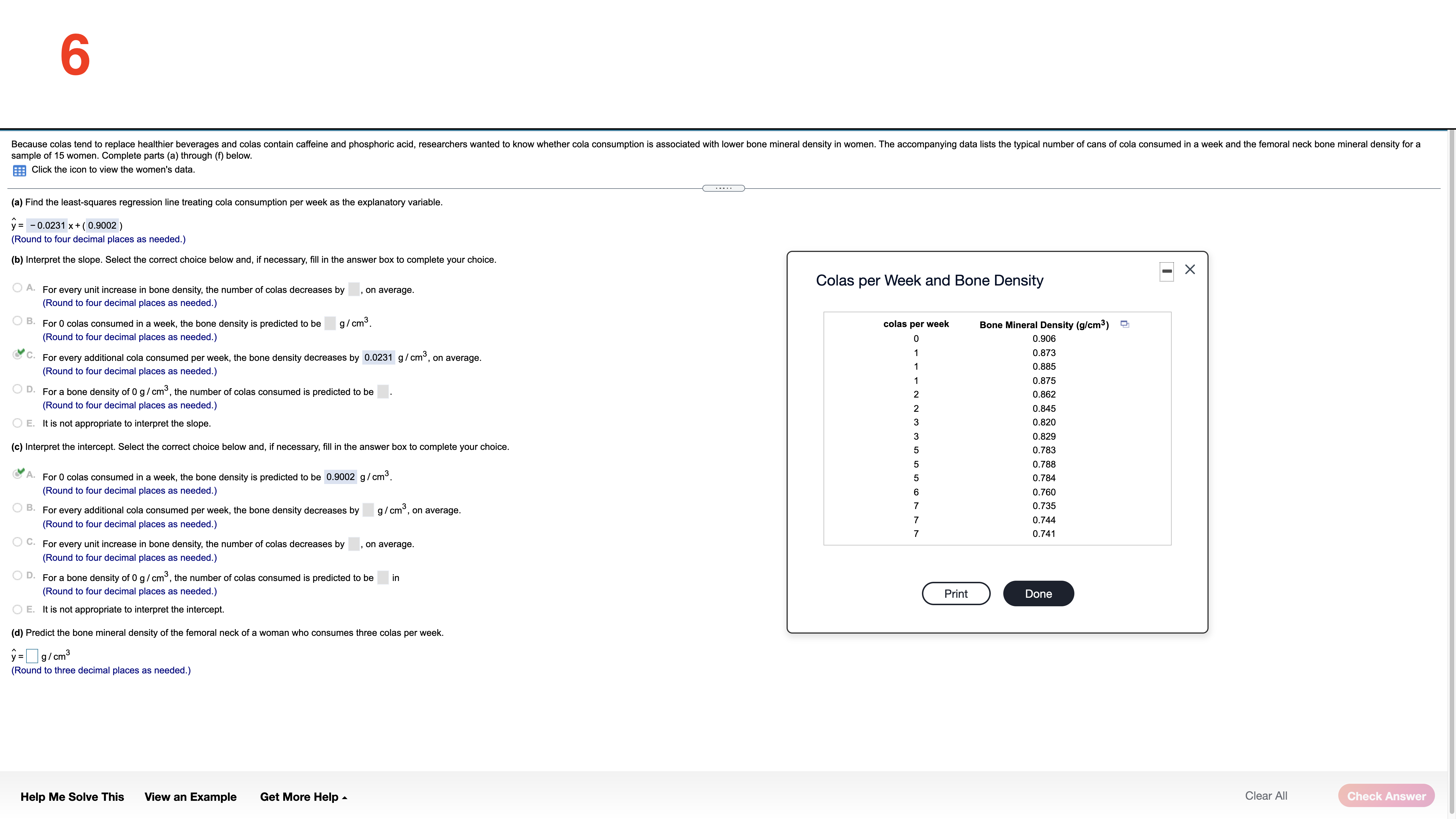
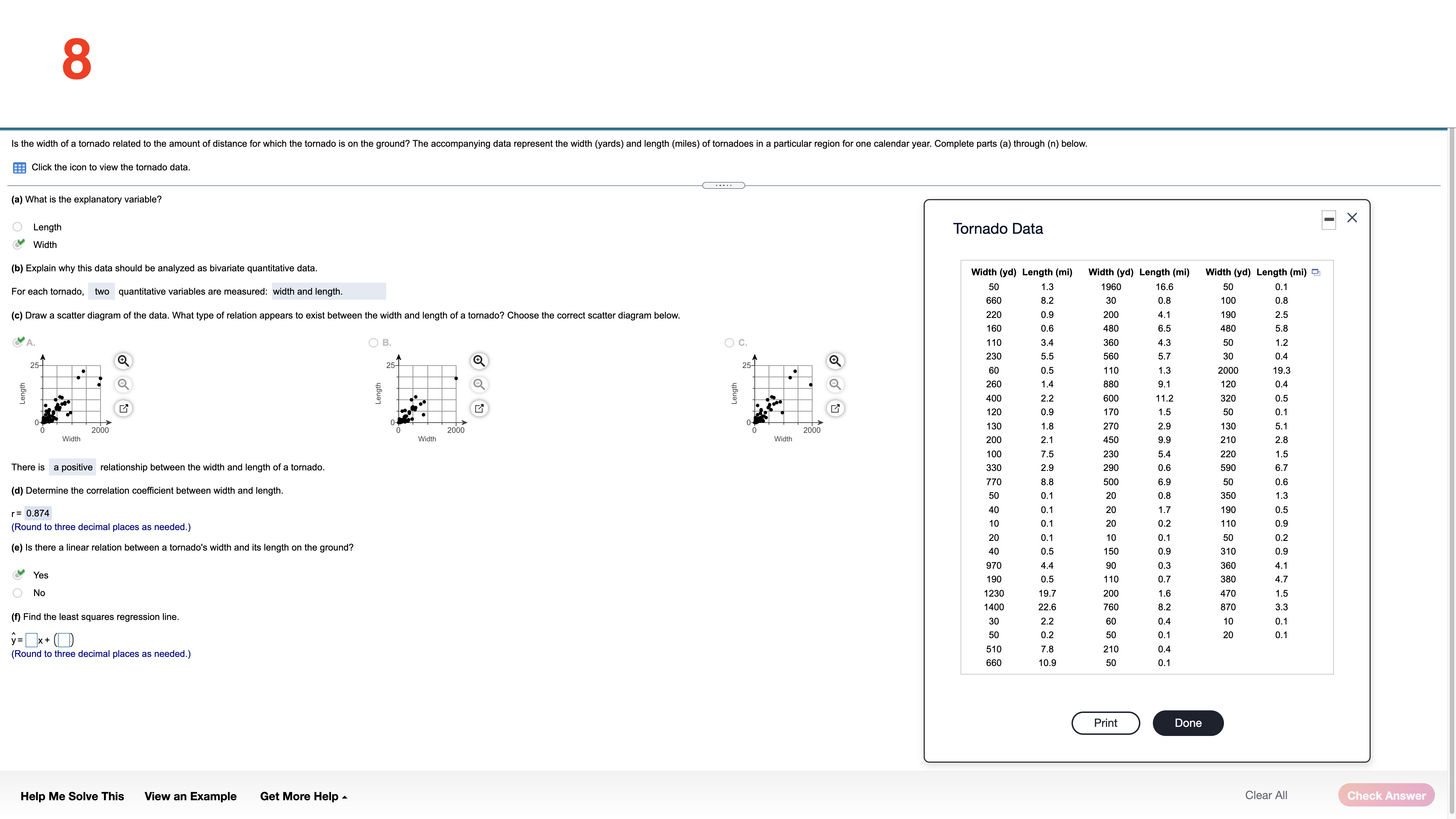
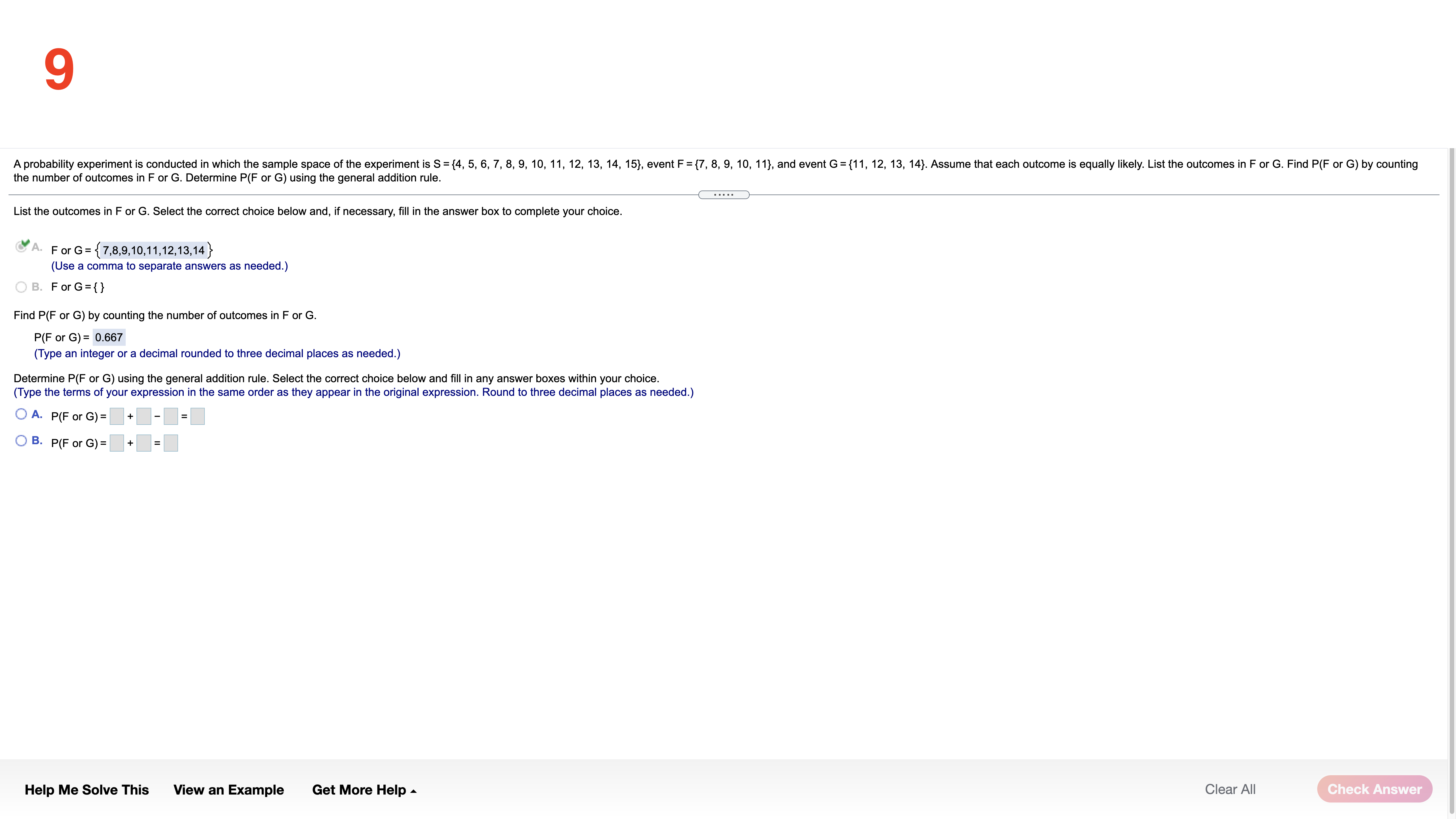
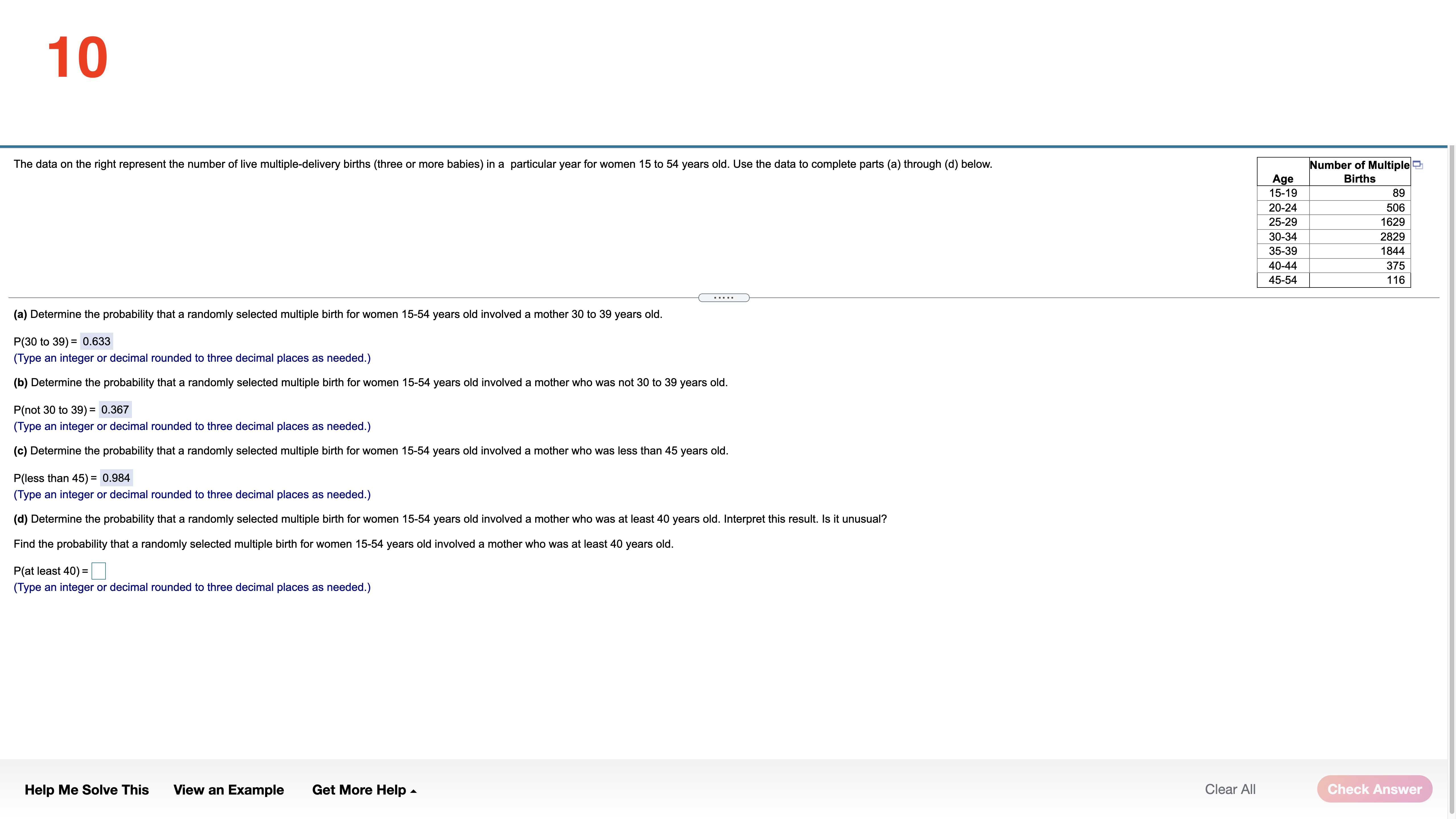
The data set below on the left represents the annual rate of return (in percent) ofeight randomly sampled bond mutual funds, and the data set (a) Determine the mean and standard deviation of each data set. below on the right represents the annual rate of return (in percent) of eight randomly sampled stock mutual funds. Use the information in the table below to complete parts (a) through (d). Then complete part (e). The mean of the data set for bond mutual funds is 2.175 . (Type an integer or decimal rounded to three decimal places as needed.) Bond mutual Stock mutual Q funds fund: The standard deviation of the data set for bond mutual funds is 0,969 . 3.0 1.6 9.2 7.4 (Type an integer or decimal rounded to three decimal places as needed.) 1.7 3.2 8.9 7.2 ' 22 2-5 8.2 7.0 The mean ofthe data set for stock mutual funds is 7313 . 1.4 1.8 7.9 6.7 (Type an integer or decimal rounded to three decimal places as needed.) The standard deviation of the data set for stock mutual funds is 0,9030 . (Type an integer or decimal rounded to three decimal places as needed.) (b) Based only on the standard deviation, stock mutual funds have more spread. (c) What proportion ofthe bond mutual funds are within one standard deviation of the mean? (Type an integer or decimal rounded to three decimal places as needed.) Help Me Solve This View an Example Get More Help A Clear All 2 Complete parts (a) through (h) for the data below. y 3 5 8 11 13 (a) By hand, draw a scatter diagram treating x as the explanatory variable and y as the response variable. Choose the correct scatter diagram below. O A B OD 10- 20- O (b) Find the equation of the line containing the points (2,3) and (7, 13). y= 2 x + (- 1) (Type integers or simplified fractions.) (c) Graph the line found in part (b) on the scatter diagram. Choose the correct graph below. OA B C. OD 20- 10-1 (d) By hand, determine the least-squares regression line. y= 1.977 x + (- 0.698 (Round to three decimal places as needed.) (e) Graph the least-squares regression line on the scatter diagram. Choose the correct graph below. B. C. OD 20- Ay 10- 10- 20- (f) Compute the sum of the squared residuals for the line found in part (b). (Round to three decimal places as needed.) Vi (1,") More Help Me Solve This View an Example Get More Help - Clear All Final Check3 Complete parts (a) through (h) for the data below. 20 40 50 60 y 100 95 90 82 70 (a) By hand, draw a scatter diagram treating x as the explanatory variable and y as the response variable. Choose the correct scatter diagram below. O A B. C. Q 100- 70- 70 10% (b) Find the equation of the line containing the points (30,95) and (60,70). y= - 6 X+ (120 ) (Type integers or simplified fractions.) (c) Graph the line found in part (b) on the scatter diagram. Choose the correct graph below. OA OB C. OD 100T 100- 10- ott (d) By hand, determine the least-squares regression line. y= - 0.73 x + (116.6) (Round to three decimal places as needed.) (e) Graph the least-squares regression line on the scatter diagram. Choose the correct graph below. OA B O C. 100 100- 701 707 70 70 (f) Compute the sum of the squared residuals for the line found in part (b). (Round to three decimal places as needed.) Help Me Solve This View an Example Get More Help - Clear All Check Answer4 The data below represent commute times (in minutes) and scores on a well-being survey. Complete parts (a) through (d) below. Commute Time (minutes), x 5 20 30 35 60 72 105 Well-Being Index Score, y 69.2 67.9 67.0 66.8 65.4 65.4 62.9 (a) Find the least-squares regression line treating the commute time, x, as the explanatory variable and the index score, y, as the response variable. y= - 0.058 x + ( 69.103 ) (Round to three decimal places as needed.) (b) Interpret the slope and y-intercept, if appropriate First interpret the slope. Select the correct choice below and, if necessary, fill in the answer box to complete your choice. O A. For every unit increase in index score, the commute time falls by , on average. Round to three decimal places as needed.) For every unit increase in commute time, the index score falls by 0.058 , on average. Round to three decimal places as needed.) O C. For an index score of zero, the commute time is predicted to be minutes. (Round to three decimal places as needed.) O D. For a commute time of zero minutes, the index score is predicted to be (Round to three decimal places as needed.) O E. It is not appropriate to interpret the slope. Interpret the y-intercept. Select the correct choice below and, if necessary, fill in the answer box to complete your choice. O A. For a commute time of zero minutes, the index score is predicted to be Round to three decimal places as needed.) O B. For every unit increase in commute time, the index score falls by 69.103 , on average. Round to three decimal places as needed.) O C. For every unit increase in index score, the commute time falls by , on average. (Round to three decimal places as needed.) O D. For an index score of zero, the commute time is predicted to be |minutes. Round to three decimal places as needed.) E. It is not appropriate to interpret the y-intercept because a commute time of zero minutes does not make sense and the value of zero minutes is much smaller than those observed in the data set. Help Me Solve This View an Example Get More Help - Clear All Final Check5 One of the biggest factors in determining the value of a home is the square footage. The accompanying data represent the square footage and selling price (in thousands of dollars) for a random sample of homes for sale in a certain region. Complete parts (a) through (h) below. Click the icon to view the housing data. (a) Which variable is the explanatory variable? Square Footage Selling Price (b) Draw a scatter diagram of the data. Choose the correct scatter diagram below. Data Table X OA O B. C 4500- 500 700- Square Footage, x Selling Price ($000s), y 2239 385.6 3169 373.4 111 187.4 1000- 349.7 150 1000 4500 2050 3188 632.8 2892 389.3 (c) Determine the linear correlation coefficient between square footage and asking price. 4141 631 .8 r= 0.903 216 6 369.9 (Round to three decimal places as needed.) 262 426.9 1778 (d) Is there a linear relation between square footage and asking price? 309.1 179 271.6 3763 682.3 NO Yes (e) Find the least-squares regression line treating square footage as the explanatory variable. Print Done y= 0.156 x + 14.9 (Round the slope to three decimal places as needed. Round the intercept to one decimal place as needed.) (f) Interpret the slope. Select the correct choice below and, if necessary, fill in the answer box to complete your choice. O A. For every additional thousand dollars in selling price, the square footage increases by square feet, on average. (Round to three decimal places as needed.) B. For every additional square foot, the selling price increases by 0.156 thousand dollars, on average. (Round to three decimal places as needed.) O C. For a house that is 0 square feet, the predicted selling price is thousand dollars. (Round to three decimal places as needed.) D. For a house that is sold for $0, the predicted square footage is. (Round to three decimal places as needed.) O E. It is not appropriate to interpret the slope (g) Is it reasonable to interpret the y-intercept? Why? Select the correct choice below and, if necessary, fill in the answer box to complete your choice. O A. Yes-a house of square feet is possible and within the scope of the model. (Type an integer or a simplified fraction.) O B. No-a house of square feet is not possible (Type an integer or a simplified fraction.) O C. No-a house of square feet is outside the scope of the model (Type an integer or a simplified fraction.) O D. No-a house of square feet is not possible and outside the scope of the model. (Type an integer or a simplified fraction.) O E. More information about the houses is necessary before deciding. Help Me Solve This View an Example Get More Help - Clear All Check Answer6 Because colas tend to replace healthier beverages and colas contain caffeine and phosphoric acid, researchers wanted to know whether cola consumption is associated with lower bone mineral density in women. The accompanying data lists the typical number of cans of cola consumed in a week and the femoral neck bone mineral density for a sample of 15 women. Complete parts (a) through (f) below. Click the icon to view the women's data. (a) Find the least-squares regression line treating cola consumption per week as the explanatory variable. y= -0.0231 x + ( 0.9002 ) (Round to four decimal places as needed.) (b) Interpret the slope. Select the correct choice below and, if necessary, fill in the answer box to complete your choice. -X Colas per Week and Bone Density O A. For every unit increase in bone density, the number of colas decreases by , on average. Round to four decimal places as needed.) O B. For 0 colas consumed in a week, the bone density is predicted to be g/cm3. colas per week Bone Mineral Density (g/cm3) (Round to four decimal places as needed. 0.906 SC. F . For every additional cola consumed per week, the bone density decreases by 0.0231 g/ cm, on average. 0.873 0.885 (Round to four decimal places as needed.) 0.875 O D. For a bone density of 0 g / cm, the number of colas consumed is predicted to be 0.862 (Round to four decimal places as needed.) 0.845 O E. It is not appropriate to interpret the slope 0.820 0.829 et the intercept. Select the correct choice below and, if necessary, fill in the answer box to complete your choice. 0.783 0.788 A. For 0 colas consumed in a week, the bone density is predicted to be 0.9002 g / cm3. 0.784 (Round to four decimal places as needed.) 0.760 O B. For every additional cola consumed per week, the bone density decreases by g/ cm, on average. 0.735 (Round to four decimal places as needed.) 0.744 0.741 O C. For every unit increase in bone density, the number of colas decreases by , on average. Round to four decimal places as needed.) O D. For a bone density of 0 g / cm , the number of colas consumed is predicted to be in Round to four decimal places as needed.) Print Done O E. It is not appropriate to interpret the intercept. (d) Predict the bone mineral density of the femoral neck of a woman who consumes three colas per week. y =g/cm3 (Round to three decimal places as needed.) Help Me Solve This View an Example Get More Help - Clear All Check Answer7 The following data represent the number of calories per serving and the number of grams of sugar per serving for a random sample of high-fiber cereals. Complete parts (a) through (d) below. Calories, x 210 230 180 160 220 20- sugar Sugar, y 17 15 16 13 H 60 calories Click the icon to view the table of critical values of the correlation coefficient. (a) A scatter diagram of the data is shown. What type of relation appears to exist between calories and sugar content? O A. There appears to be a strong nonlinear relationship between calories and sugar content. O B. There appears to be a strong linear relationship between calories and sugar content. CC. There appears to be little or no relationship between calories and sugar content. (b) Determine the correlation coefficient between calories and sugar content. Table of Critical Values of the Correlation Coefficient X The correlation coefficient is - 0.615 . (Type an integer or decimal rounded to three decimal places as needed.) Determine the critical value for the correlation coefficient. 0.997 0.878 0.950 (Type an integer or decimal rounded to three decimal places as needed.) O VOU A W : 0.878 Is there a linear relation between calories and sugar content? 0.811 0.754 O A. Since the absolute va coefficient is less than the critical value, there is a linear relation between calories and sugar content. 0.707 9 B. Since the absolute value of the correlation coefficient is greater than the critical value, there is not a linear relation between calories and sugar content. 0.666 10 0.632 C. Since the absolute value of the correlation coefficient is less than the critical value, there is not a linear relation between calories and sugar content. 11 0.602 O D. Since the absolute value of the correlation coefficient is greater than the critical value, there is a linear relation between calories and sugar content. 12 0.576 13 0.553 (c) Suppose that we add another cereal, which has 50 calories and 3 grams of sugar per serving, to the data set. Redraw the scatter diagram of the data with this cereal included. Choose the correct plot below. 0.532 0.514 O B. J C. 0.497 20- 250- 20- 17 0.482 . 18 0.468 sugar calories 19 0.456 20 0.444 20 250 calories calories sugar Recompute the correlation coefficient Print Done The new correlation coefficient is 0.816. (Type an integer or decimal rounded to three decimal places as needed.) Determine the critical value for the correlation coefficient. (Type an integer or decimal rounded to three decimal places as needed.) Help Me Solve This View an Example Get More Help - Clear All Check Answer8 Is the width of a tornado related to the amount of distance for which the tornado is on the ground? The accompanying data represent the width (yards) and length (miles) of tornadoes in a particular region for one calendar year. Complete parts (a) through (n) below. Click the icon to view the tornado data. (a) What is the explanatory variable? -X O Length Tornado Data Width (b) Explain why this data should be analyzed as bivariate quantitative data. Width (yd) Length (mi) Width (yd) Length (mi) Width (yd) Length (mi) For each tornado, two quantitative variables are measured: width and length. 60 1.3 1960 16. 50 0.1 8.2 30 0.8 10 0.8 (c) Draw a scatter diagram of the data. What type of relation appears to exist between the width and length of a tornado? Choose the correct scatter diagram below. 220 0.9 200 4.1 190 25 160 0.6 480 6.5 480 5.8 O B. OC. 110 3.4 360 4.3 50 1 .2 230 5.5 560 5.7 30 0.4 25-1 25- 60 0.5 110 1 .3 2000 19.3 260 1.4 880 9.1 120 0.4 Length Length Length 400 2.2 600 11.2 320 0.5 120 2.9 170 1.5 50 0.1 2000 2000 2000 130 1.8 270 2.9 130 5.1 Width Width Width 200 2.1 450 9.9 210 2.8 100 7.5 230 5.4 220 1.5 There is a positive relationship between the width and length of a tornado. 330 2.9 290 0.6 590 6.7 770 8.8 500 6.9 50 0.6 (d) Determine the correlation coefficient between width and length. 50 0.1 20 0 .8 350 1.3 r= 0.874 40 0.1 20 1.7 190 0.5 (Round to three decimal places as needed.) 10 0.1 20 0.2 110 0.9 20 0.1 10 0.1 50 0.2 (e) Is there a linear relation between a tornado's width and its length on the ground? 40 0.5 150 0.9 310 0.9 970 4.4 90 0.3 360 4.1 Yes 190 0.5 110 0.7 380 4.7 No 1230 19.7 200 1.6 1.5 400 22.6 760 8.2 870 3.3 (f) Find the least squares regression line. 30 2.2 60 0.4 0.1 y= x + () 50 0.2 50 0.1 20 01 (Round to three decimal places as needed.) 510 7.8 210 0.4 099 10.9 50 0.1 Print Done Help Me Solve This View an Example Get More Help - Clear All Check AnswerCO A probability experiment is conducted in which the sample space of the experiment is S = {4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15), event F = {7, 8, 9, 10, 11}, and event G= {11, 12, 13, 14). Assume that each outcome is equally likely. List the outcomes in F or G. Find P(F or G) by counting the number of outcomes in F or G. Determine P(F or G) using the general addition rule. List the outcomes in F or G. Select the correct choice below and, if necessary, fill in the answer box to complete your choice. A. For G= { 7,8,9, 10, 11, 12, 13, 14 } (Use a comma to separate answers as needed.) O B. For G= { } Find P(F or G) by counting the number of outcomes in F or G. (F or G) = 0.667 Type an integer or a decimal rounded to three decimal places as needed.) Determine P(F or G) using the general addition rule. Select the correct choice below and fill in any answer boxes within your choice. (Type the terms of your expression in the same order as they appear in the original expression. Round to three decimal places as needed.) O A. P(F or G) = + O B. P(F or G) = += Help Me Solve This View an Example Get More Help - Clear All Check Answer10 The data on the right represent the number of live multiple-delivery births (three or more babies) in a partioular year for women 15 lo 54 years old. Use the data to complete parts (a) through (d) below. Number of Multiple% A a Birth: 1 5919 89 20-24 506 25-29 1629 3034 2829 35-39 1844 40-44 375 45-54 1 16 (9) Determine the probability that a randomly selected multiple birth lor women 1554 years old involved a mother 30 to 39 years old. mo to 39): 0.633 (Type an integer or decimal rounded to three decimal places as needed.) (h) Determine the probability that a randomly selected multiple birth tor women 15-54 years old involved a mother who was not 30 to 39 years old. P(not so to 39)= 0.367 (Type an integer or decimal rounded to three decimal places as needed.) is) Determine the probability that a randomly selected multiple birth (or women 15-54 years old involved a mother who was less than 45 years old. P(less than 45) = 0384 (Type an integer or decimal rounded to three decimal places as needed.) (d) Determine the probability that a randomly selected multiple birth for women 1554 years old involved a mother who was at least 40 years old. Interpret this result. Is it unusual? Find the probability that a randomly selected mullipla birth for women 15-54 years old involved a mother who was at least 40 years old. F(at least 40) = (Type an integer or decimal rounded to three decimal places as needed.) Help Me Solve This View an Example Get More Help A Clear All