Need it done in Excel please thank you

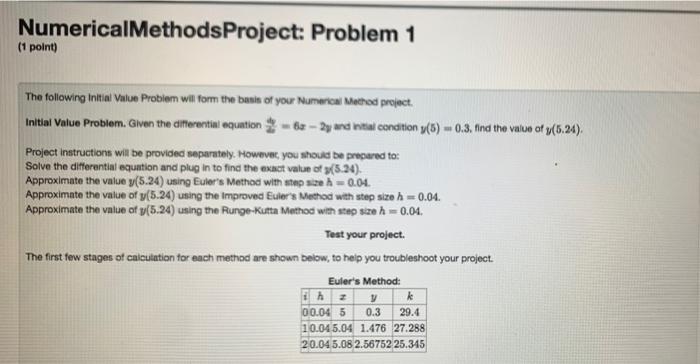
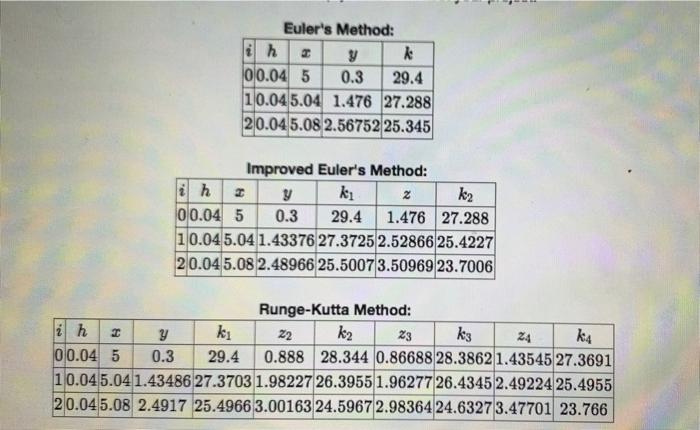
Part 1: Use technology (see "Technology Options" below) to approximate the solution to your Initial Value Problem using Euler's Method, the Improved Euler's Method, and the Runge-Kutta Method. See "Project Requirements" below for more details. Part II. Find the exact solution y(x) to the Initial Value Problem and use it to determine the value requested in the problem. Round your answer to 8 decimal places. Type or write your answer to this part and submit it with your project. Part III. Compare the exact value obtained in Part II to the three numerical approximations obtained in Part I. How many correct decimal digits did each method produce? Which method was the most accurate? Type or write your answer to this part and submit it with your project. NumericalMethodsProject: Problem 1 (1 point) The following initial Value Problem will form the basis of your Numerical Method project. Inital Value Problem. Given the differential equation - 8 - 2y and inal condition y(8) - 0.3, Ind the value of y(5:24). Project instructions will be provided separately. However, you should be prepared to: Solve the differential equation and plug in to find the exact value of 3(5.24). Approximate the value y(5.24) using Euler's Method with step size = 0.04. Approximate the value of y(5.24) using the improved Euler's Method with step size h = 0.04. Approximate the value of y(5.24) using the Runge-Kutta Method with stepsze h = 0.04. Test your project. The first few stages of calculation for each method are shown below, to help you troubleshoot your project. Euler's Method: Az y k 00.04 5 0.3 29.4 10.04 5.04 1.476 27.288 20.04 5.08 2.56752 25.345 Euler's Method: ih y k 0 0.04 5 0.3 29.4 10.04 5.04 1.476 27.288 20.045.08 2.56752 25.345 Improved Euler's Method: lih I y ki k2 0 0.04 5 0.3 29.4 1.476 27.288 10.04 5.04 1.43376 27.3725 2.52866 25.4227 20.04 5.08 2.48966 25.50073.50969 23.7006 Runge-Kutta Method: 2 h y ki 22 k2 23 k3 24 k4 0 0.04 5 0.3 29.4 0.888 28.344 0.86688 28.3862 1.43545 27.3691 10.045.04 1.43486 27.3703 1.98227 26.3955 1.96277 26.4345 2.49224 25.4955 20.045.08 2.4917 25.4966 3.00163 24.59672.9836424.6327 3.47701 23.766 Part 1: Use technology (see "Technology Options" below) to approximate the solution to your Initial Value Problem using Euler's Method, the Improved Euler's Method, and the Runge-Kutta Method. See "Project Requirements" below for more details. Part II. Find the exact solution y(x) to the Initial Value Problem and use it to determine the value requested in the problem. Round your answer to 8 decimal places. Type or write your answer to this part and submit it with your project. Part III. Compare the exact value obtained in Part II to the three numerical approximations obtained in Part I. How many correct decimal digits did each method produce? Which method was the most accurate? Type or write your answer to this part and submit it with your project. NumericalMethodsProject: Problem 1 (1 point) The following initial Value Problem will form the basis of your Numerical Method project. Inital Value Problem. Given the differential equation - 8 - 2y and inal condition y(8) - 0.3, Ind the value of y(5:24). Project instructions will be provided separately. However, you should be prepared to: Solve the differential equation and plug in to find the exact value of 3(5.24). Approximate the value y(5.24) using Euler's Method with step size = 0.04. Approximate the value of y(5.24) using the improved Euler's Method with step size h = 0.04. Approximate the value of y(5.24) using the Runge-Kutta Method with stepsze h = 0.04. Test your project. The first few stages of calculation for each method are shown below, to help you troubleshoot your project. Euler's Method: Az y k 00.04 5 0.3 29.4 10.04 5.04 1.476 27.288 20.04 5.08 2.56752 25.345 Euler's Method: ih y k 0 0.04 5 0.3 29.4 10.04 5.04 1.476 27.288 20.045.08 2.56752 25.345 Improved Euler's Method: lih I y ki k2 0 0.04 5 0.3 29.4 1.476 27.288 10.04 5.04 1.43376 27.3725 2.52866 25.4227 20.04 5.08 2.48966 25.50073.50969 23.7006 Runge-Kutta Method: 2 h y ki 22 k2 23 k3 24 k4 0 0.04 5 0.3 29.4 0.888 28.344 0.86688 28.3862 1.43545 27.3691 10.045.04 1.43486 27.3703 1.98227 26.3955 1.96277 26.4345 2.49224 25.4955 20.045.08 2.4917 25.4966 3.00163 24.59672.9836424.6327 3.47701 23.766









