need solution of B.com 2nd year maths problem
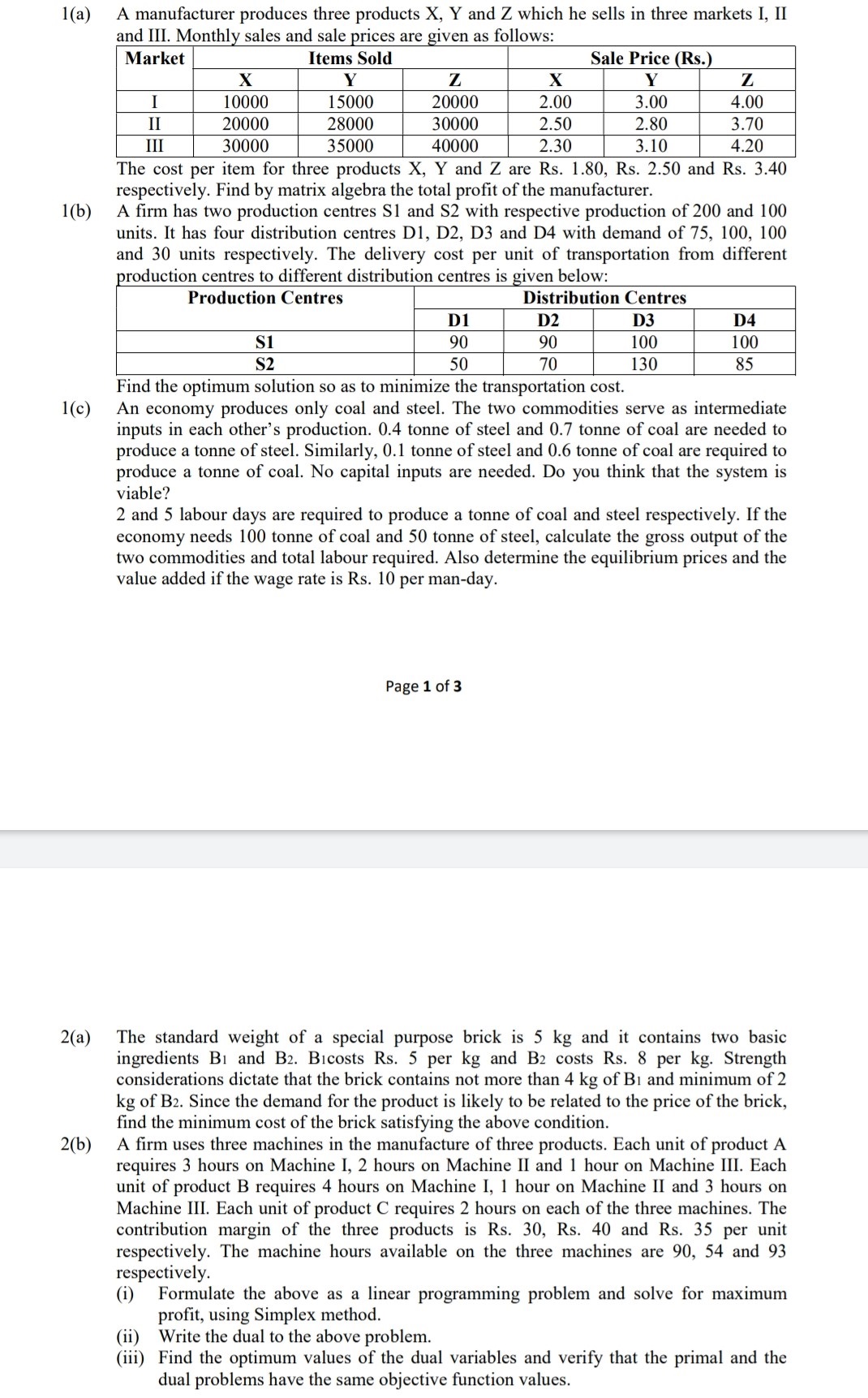
1 (a) 1(b) 1(6) A manufacturer produces three products X, Y and Z which he sells in three markets I, II and III. Monthly sales and sale prices are given as follows: Market Items Sold Sale Price (Rs. X Y l Z X Y Z I 10000 15000 l 20000 2.00 3.00 4.00 11 20000 28000 i 30000 2.50 2.80 3.70 111 30000 35000 l 40000 2.30 3.10 4.20 The cost per item for three products X, Y and Z are Rs. 1.80, Rs. 2.50 and Rs. 3.40 respectively. Find by matrix algebra the total prot of the manufacturer. A rm has two production centres SI and 82 with respective production of 200 and 100 units. It has four distribution centres D1, D2, D3 and D4 with demand of 75, 100, 100 and 30 units respectively. The delivery cost per unit of transportation from different Production Centres Distribution Centres l l D1 [)2 | D3 I 114 51 l 90 90 | 100 I 100 froduction centres to different distribution centres is given below: 52 l 50 70 I 130 I 85 Find the optimum solution so as to minimize the transportation cost. An economy produces only coal and steel. The two commodities serve as intermediate inputs in each other's production. 0.4 tonne of steel and 0.7 tonne of coal are needed to produce a tonne of steel. Similarly, 0.1 tonne of steel and 0.6 tonne of coal are required to produce a tonne of coal. No capital inputs are needed. Do you think that the system is viable? 2 and 5 labour days are required to produce a tonne of coal and steel respectively. If the economy needs 100 tonne of coal and 50 tonne of steel, calculate the gross output of the two commodities and total labour required. Also determine the equilibrium prices and the value added if the wage rate is Rs. 10 per man-day. Page 1 of 3 2(a) 2(b) The standard weight of a special purpose brick is 5 kg and it contains two basic ingredients Br and B2. Brcosts Rs. 5 per kg and B2 costs Rs. 8 per kg. Strength considerations dictate that the brick contains not more than 4 kg of B1 and minimum of 2 kg of 32. Since the demand for the product is likely to be related to the price of the brick, nd the minimum cost of the brick satisfying the above condition. A rm uses three machines in the manufacture of three products. Each unit of product A requires 3 hours on Machine I, 2 hours on Machine II and 1 hour on Machine III. Each unit of product B requires 4 hours on Machine I, 1 hour on Machine II and 3 hours on Machine III. Each unit of product C requires 2 hours on each of the three machines. The contribution margin of the three products is Rs. 30, R5. 40 and Rs. 35 per unit respectively. The machine hours available on the three machines are 90, 54 and 93 respectively. (i) Formulate the above as a linear programming problem and solve for maximum profit, using Simplex method. (ii) Write the dual to the above problem. (iii) Find the optimum values of the dual variables and verify that the primal and the dual problems have the same objective function values