NEED SOLVED IN JAVA

the topic of this project is sorting. The goal is two-fold: First, you will acquire hands-on experience with the implementation of an advanced sorting algorithm. Second, you will learn how to use sorting to solve a practical problem efficiently. In the first part, you will implement an enhanced version of quicksort. In the second part, you will use sorting to solve a real-world application.

Part 1 - Fast three-way partitioning. (J. Bentley and D. McIlroy)

Basic Algorithm

You will implement an entropy-optimal sort Quick3wayBM.java based on keeping equal keys at both the left and right ends of the sub-array a[lo,...,hi]. Practically, you need to maintain indices that enforce the following invariants:

indices p and q are such that a[lo,...,p] and a[q,...,hi] are all equal to a[lo]

an index i is such that a[p+1,...,i-1] are all less than a[lo]

an index j is such that a[j+1,...,q-1] are all greater than a[lo]

These notations are illustrated below.

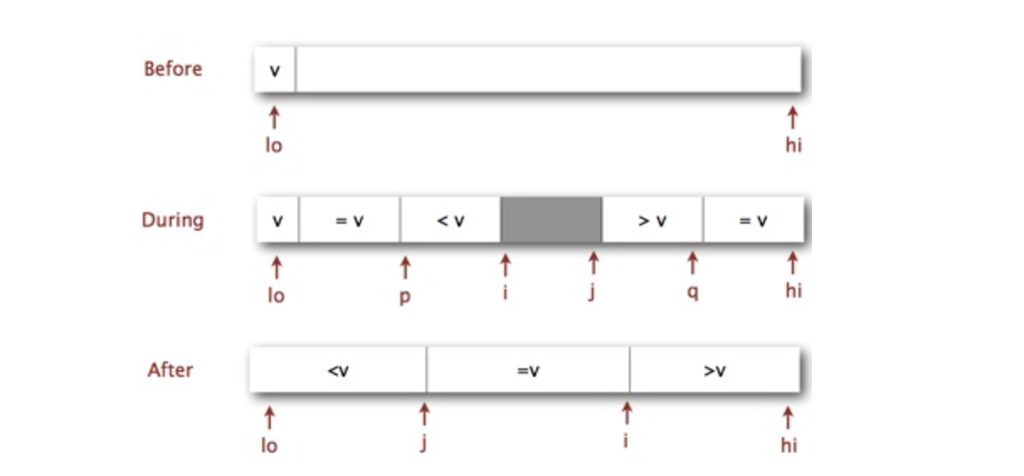
In your code, you should add to the inner partitioning loop code to swap a[i] with a[p+1] (and increment p) if it is equal to v, and to swap a[j] with a[q-1] (and decrement q) if it is equal to v, after the usual comparisons of a[i] and a[j] with v. The partitioning should terminate when (i > j), and you should treat (i == j) as a special case where you should just simply advance j by one and break the loop. After the partitioning loop has terminated, add code to swap the items with equal keys into position, whereby you will have to swap(lo, j) and then swap(lo+1, j-1) ... swap(j-k, p). Similarly you have to do the same for the elements to the right of j, swap(j+1, hi) ... swap(j+w, q), whereby k (resp. w) are the number of duplicate elements to the left (resp. right) of the sub-array.

Improvements

In your code, you must implement the following improvements:

Cutoff to insertion sort. It usually pays off to switch to insertion sort for tiny arrays. The optimum value of the cutoff in your code MUST be 8.

Median-of-three partitioning. A second improvement is to use the median of a small sample of items taken from the array as the partitioning item. Doing so will give a slightly better partition, but at the cost of computing the median. It turns out that most of the available improvement comes from choosing a sample of size 3 (and then partitioning on the middle item). You should ONLY use this improvement if the current number of elements to sort is ( 40).

Tukey ninther. Use the Tukey ninther technique as partitioning element when the previous optimizations do not apply.

Note: Finding the Median

To find the median in Median-of-3 (resp. Tukey ninther) you should pick three (resp. nine) elements spaced in your sub-array by floor((N-1)/2) (resp. floor((N-1)/8)) starting from the first element, where N is the number of elements in the sub-array. Note that the 3rd (resp. 9th) selected element may not be the last element.

Input / Output

Your program should read the input from StdIn.java. It should process the input using the following command:

 %java -cp .:stdlib.jar:algs4.jar Quick3wayBM  
The file contains a list of numbers in the format (). The first number is the number of elements in the file.
 
In each recursive sorting call of the array you have to output the following as a tuple following the exact format shown below. Your program should simply print the output to the command line. In the case you used the insertion sort just output:
 
 (Insertion Sort, , ) 
 
Otherwise, you should output:
 
 (, , , 
 
, , , , )
 
where will be either "Median of 3" or "Tukey Ninther", depending on the case.
 
As an example of the former scenario, your program should output:
 
 (Insertion Sort, 1, 4)  
 
As two examples of the latter scenario, your program should output:
 
 (Median of 3, 1, 10, 4, 15, 16, 20, 25) (Tukey Ninther, 6, 20, 4, 18, 17, 50, 70)  
 
This output should take place before you move the equal values from the two ends of the array to the middle.
 
Step-by-step output
 
In addition to the above output, you will augment your Quick3wayBM.java code and submit another file that provides a trace of the sorting steps, called Quick3wayBM_V.java. It should process the input just as above, with the command:
 
 %java -cp .:stdlib.jar:algs4.jar Quick3wayBM_V  
 
Print to standard output the elements, separated by spaces, in their current order, with one line per recursive sorting call. The first line should be the original order of the elements, and the last line should be the sorted order of the elements. At each step, output the elements after moving the equal elements in the two ends of the array to the middle.
  Before lo hi During  V lo hi After =v lo hi