Need some help explaining an R Based question

Just need some help to start on this

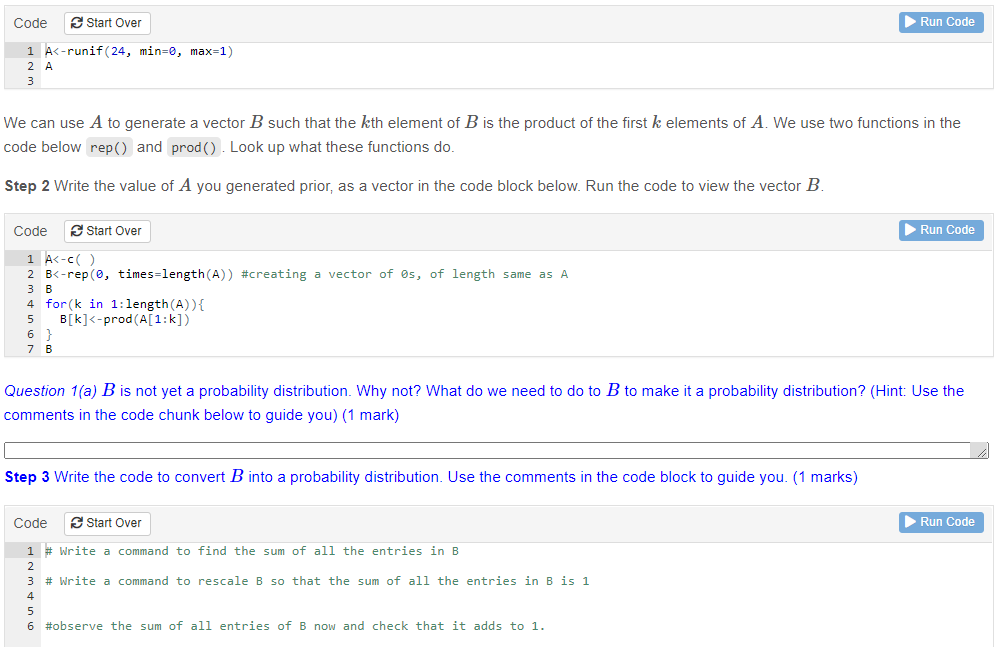
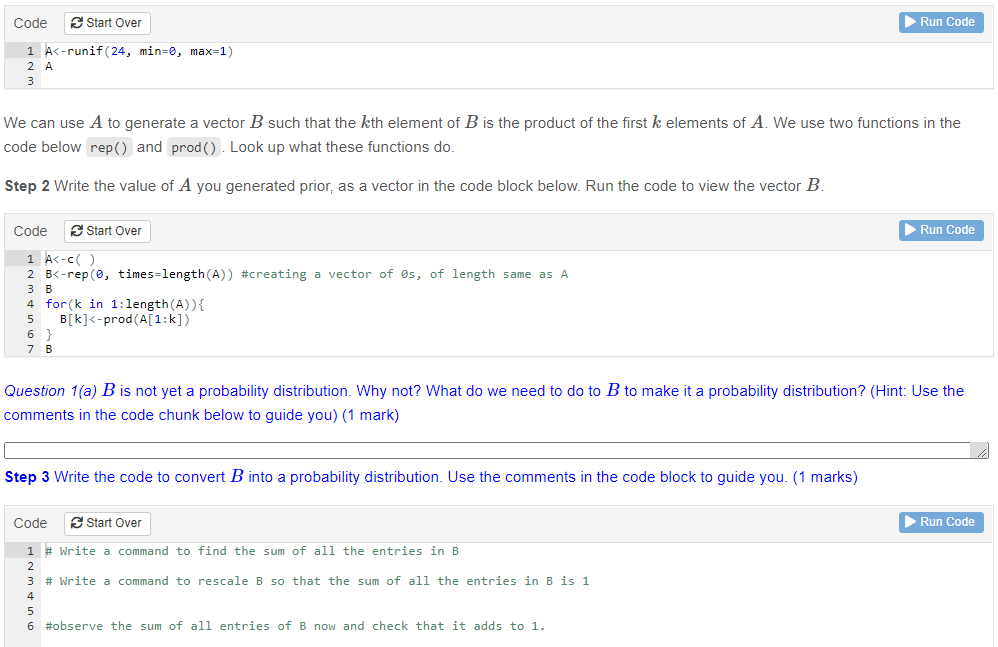
Let us consider a scenario where an attacker has a maximum of 24 attempts to guess a key. In this case, the index ofthe trial that an attacker must make to successfully guess the key can be considered a random variable X, that takes values from 1 to 24. The key is distributed in such a way that the probability of a succesle guess for the attacker in each trial is different. The vector of probabilities of success for each that is called the probability distribution PI of the random variable X. P3:{X = 1} represents the probability of success in the rst trail, P${X = 2) represents the probability of success in the second trial and so on_. Let us now generate the probability distribution Pa: for the random variable X such that Pa: obeys the rule Pa: [1] 1:} Pic[2] >. . . i.e. the highest chance of success for the attacker is in the rst trial and at every subsequent trial the probability of success drops. We do this using a pseudo random number generator in R and the following steps. step 1: The R command runiff) in the code block below generates 24 random numbers between I) and 1, drawn from a uniform distribution. Notice that every time you run the code block you will get a different vector A. lCode | 3 Start Over | I. 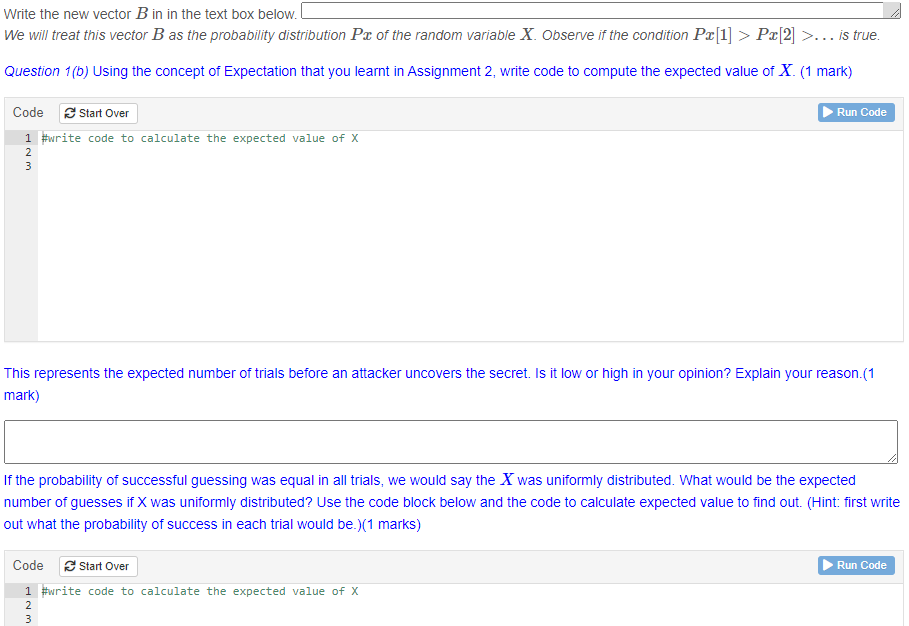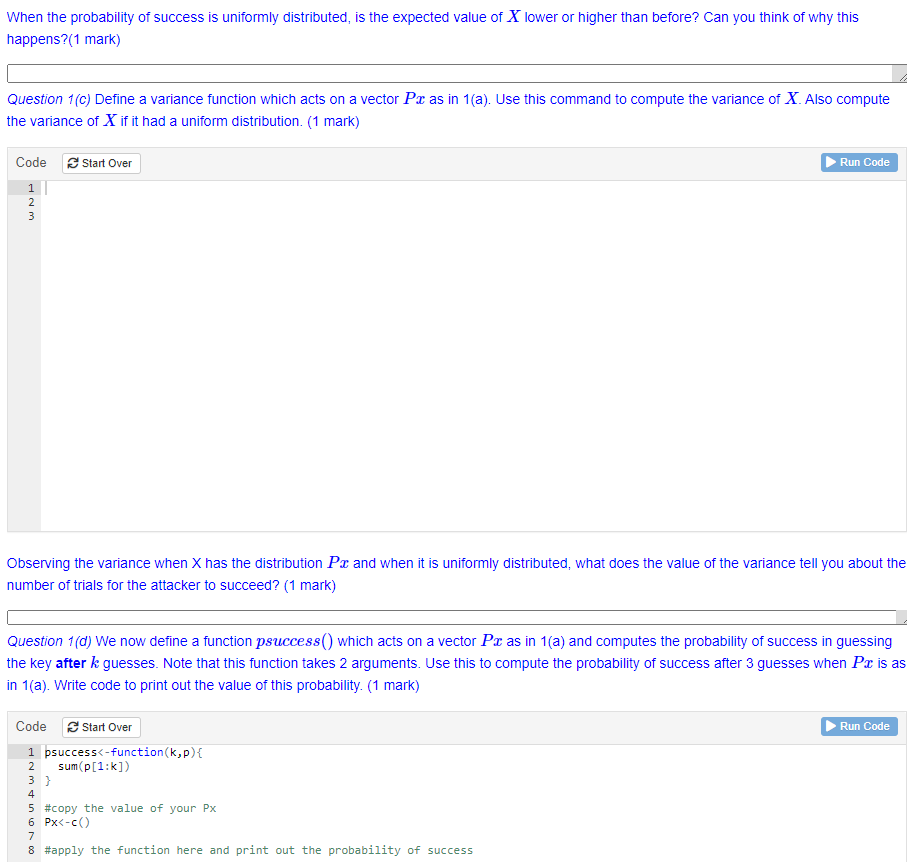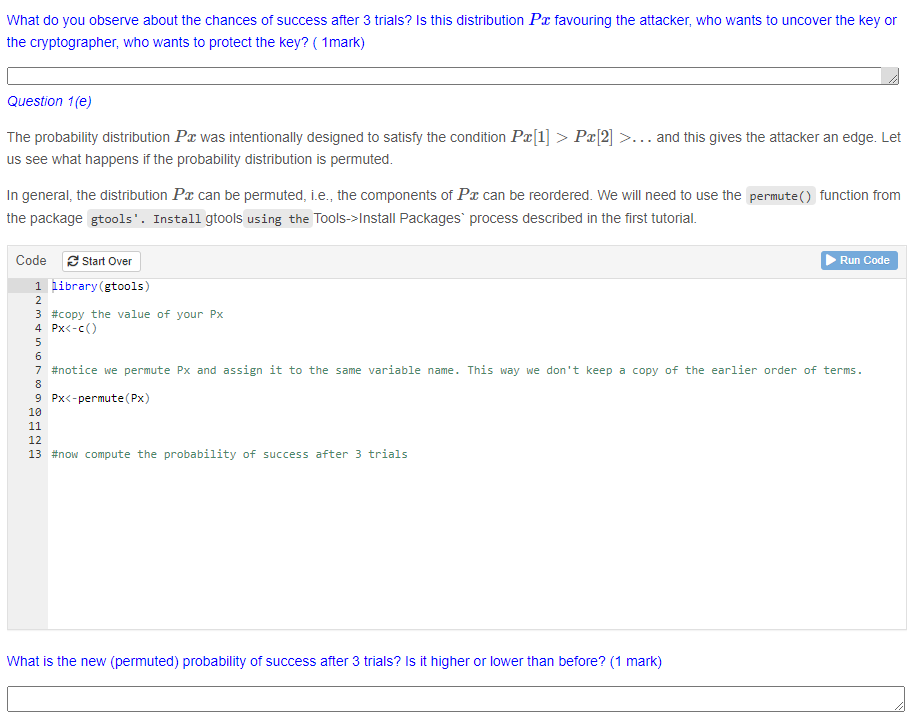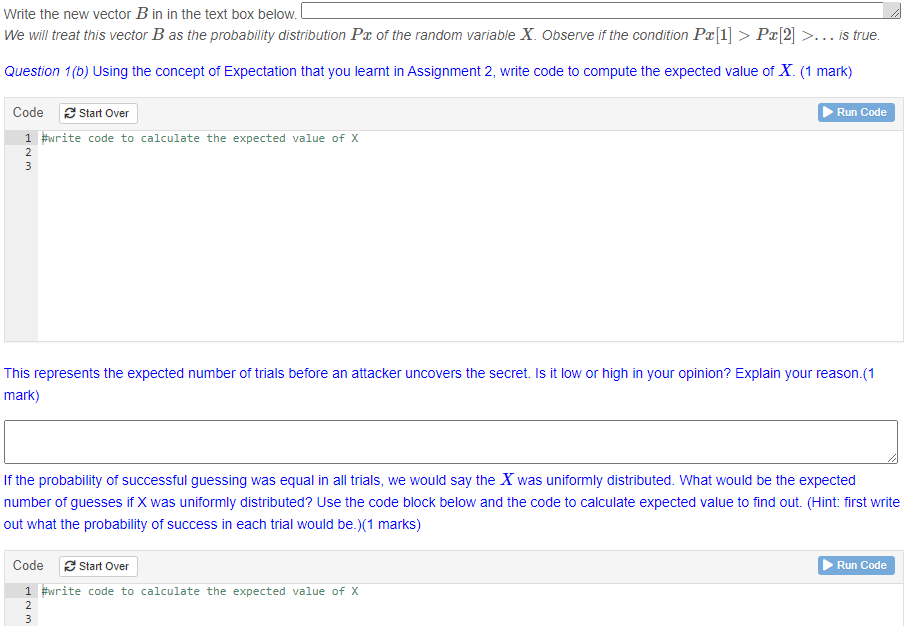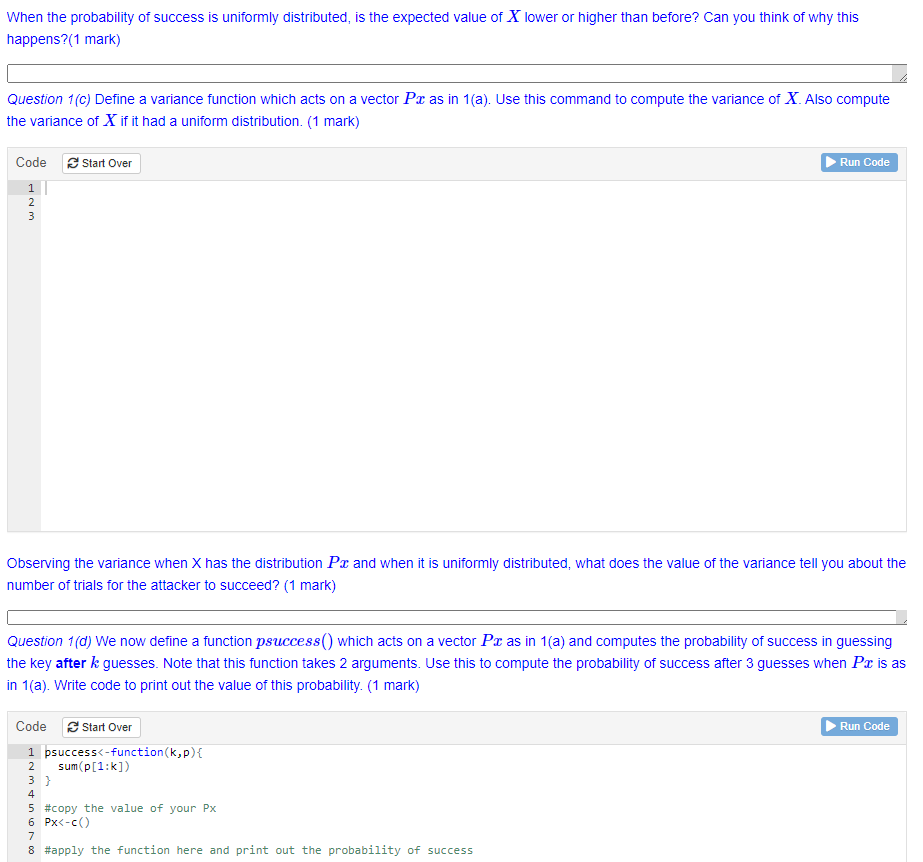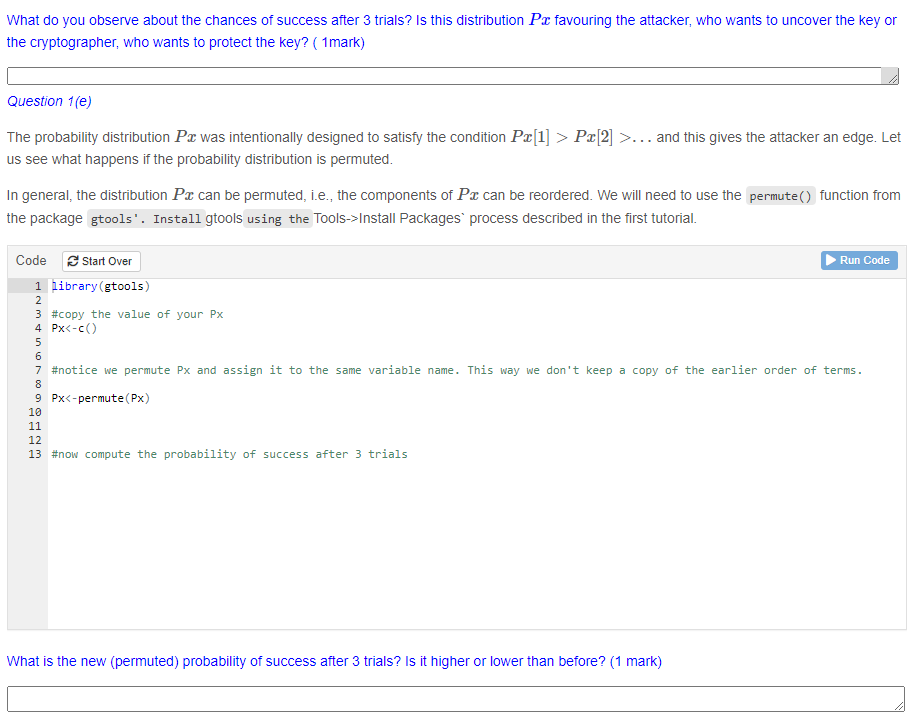Run Code 1 Px[2] >... is true. Question 1(b) Using the concept of Expectation that you learnt in Assignment 2, write code to compute the expected value of X. (1 mark) Code Start Over Run Code 1 #write code to calculate the expected value of X This represents the expected number of trials before an attacker uncovers the secret. Is it low or high in your opinion? Explain your reason.(1 mark) If the probability of successful guessing was equal in all trials, we would say the X was uniformly distributed. What would be the expected number of guesses if X was uniformly distributed? Use the code block below and the code to calculate expected value to find out. (Hint: first write out what the probability of success in each trial would be.)(1 marks) Code Start Over Run Code #write code to calculate the expected value of XWhen the probability of success is uniformly distributed, is the expected value of X lower or higher than before? Can you think of why this happens?(1 mark) Question 1(c) Define a variance function which acts on a vector Px as in 1(a). Use this command to compute the variance of X. Also compute the variance of X if it had a uniform distribution. (1 mark) Code Start Over Run Code 1 Observing the variance when X has the distribution Pa and when it is uniformly distributed, what does the value of the variance tell you about the number of trials for the attacker to succeed? (1 mark) Question 1(d) We now define a function psuccess() which acts on a vector Pr as in 1(a) and computes the probability of success in guessing the key after / guesses. Note that this function takes 2 arguments. Use this to compute the probability of success after 3 guesses when Px is as in 1(a). Write code to print out the value of this probability. (1 mark) Code Start Over Run Code psuccess Px 2] >. . . and this gives the attacker an edge. Let us see what happens if the probability distribution is permuted. In general, the distribution Pax can be permuted, i.e., the components of Px can be reordered. We will need to use the permute() function from the package gtools' . Install gtools using the Tools->Install Packages' process described in the first tutorial. Code Start Over Run Code 1 library (gtools) #copy the value of your Px 4 PX