Need summary for this . Make sure someone who understands it and summarize it in 2 pages with some summary of the data also

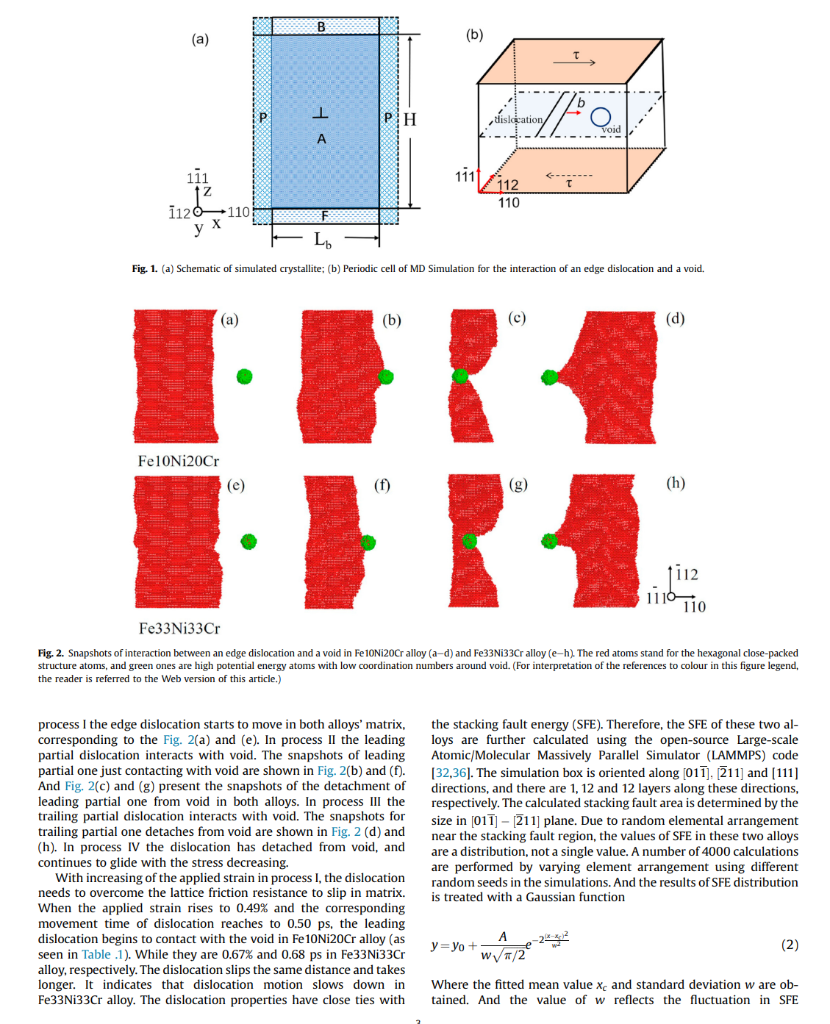
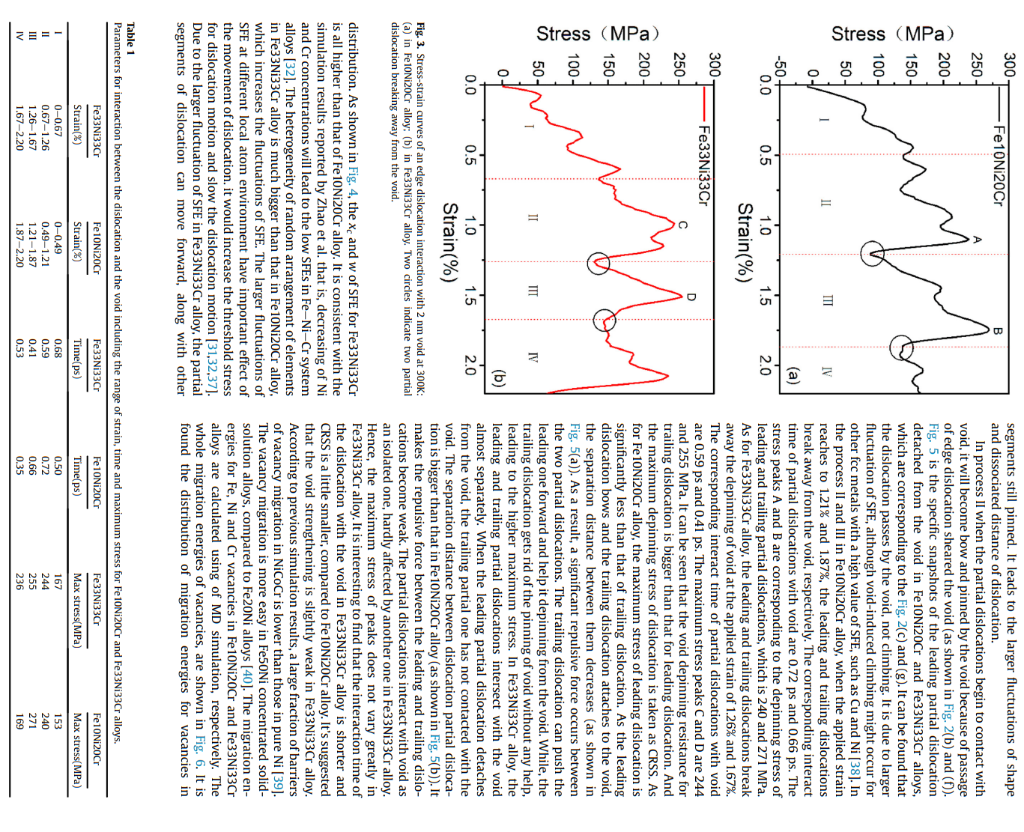
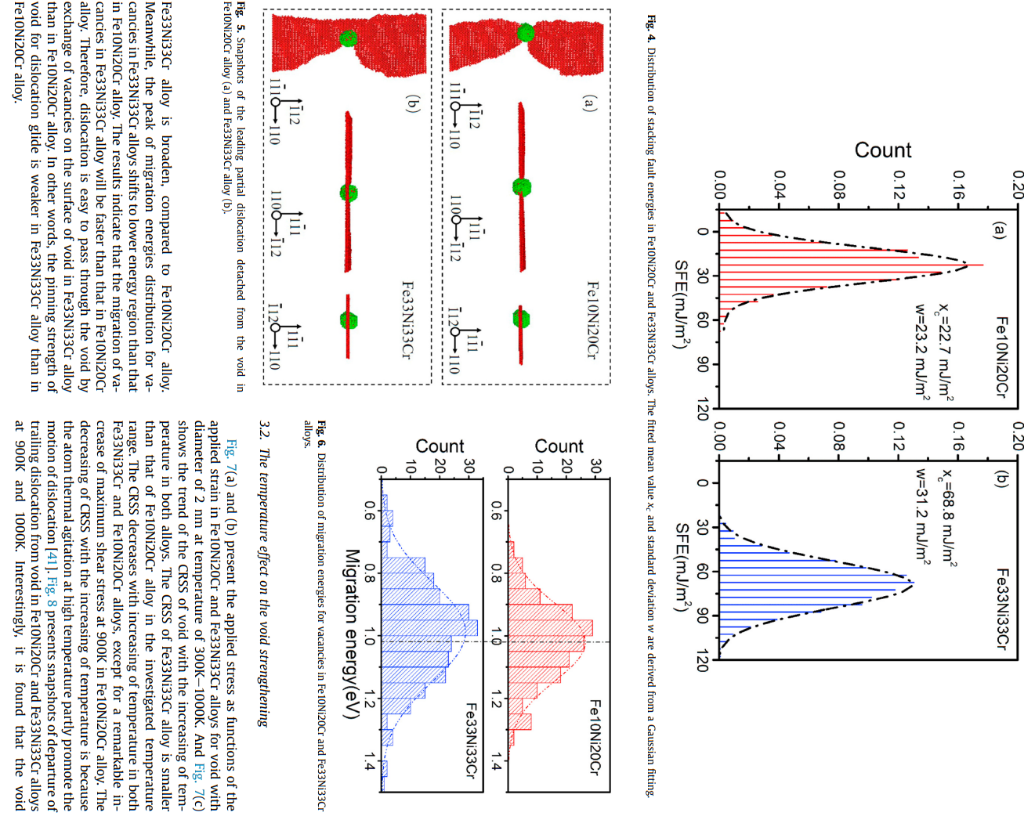
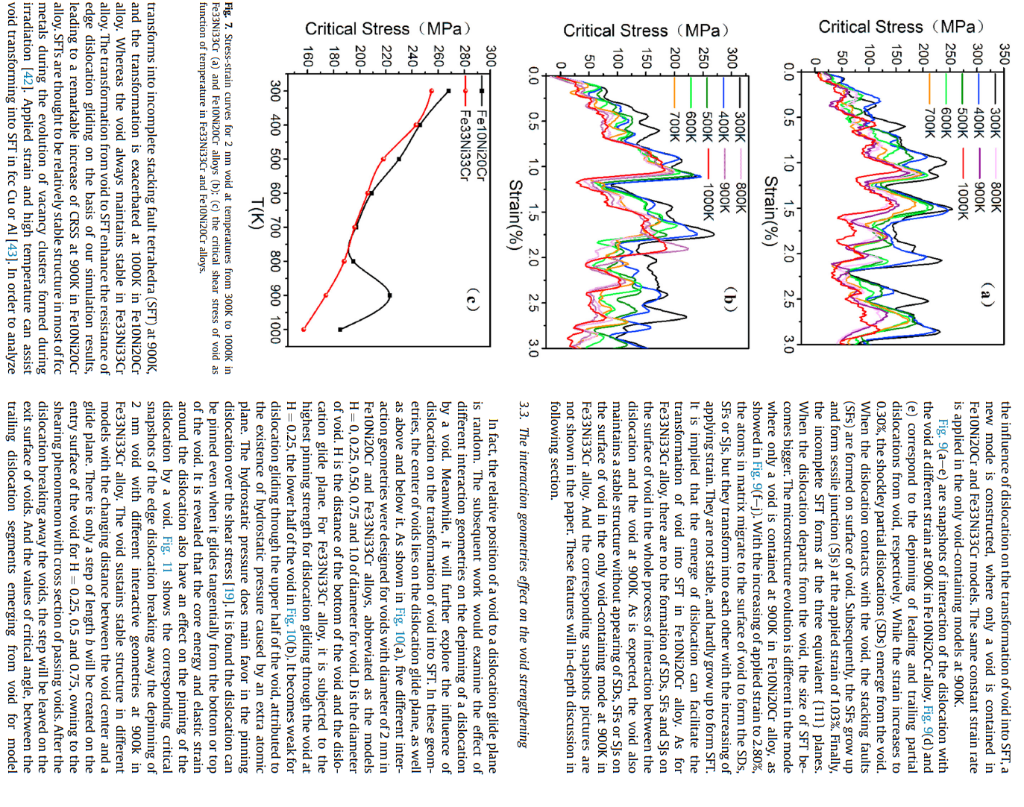
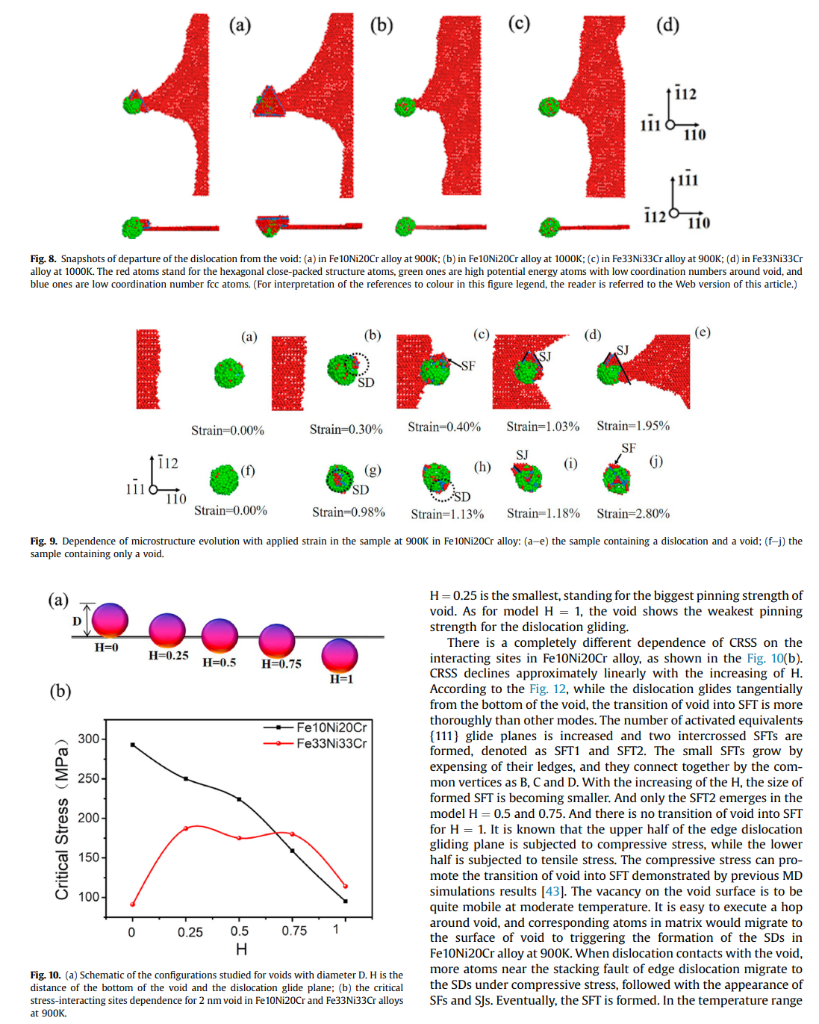
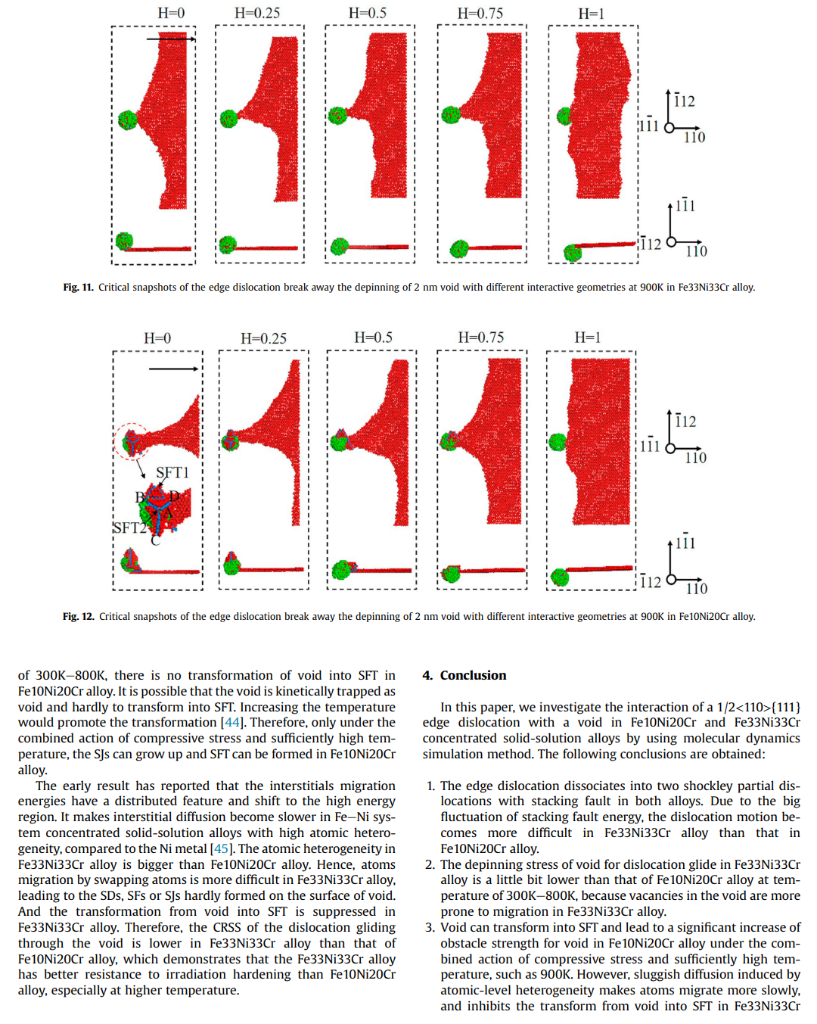
Article history: The interactions of a 1/2{111} edge dislocation with a void in Fe10Ni20Cr and Fe33Ni33Cr Received 3 August 2020 concentrated solid-solution alloys are investigated by using molecular dynamics simulation method. The Received in revised form edge dislocation dissociates into two shockley partial dislocations with stacking fault in both alloys. 28 September 2020 Compared to the Fe10Ni20Cr alloy, the dislocation motion becomes difficult in Fe33Ni33Cr alloy due to Accepted 11 October 2020 Available online 15 October 2020 the big fluctuation of stacking fault energy. The obstacle strength for a void with diameter of 2 nm in Fe33Ni33Cr alloy is slightly weaker than that in Fe10Ni20Cr alloy at temperature range from 300K to Keywords: 800K. It is attributed to easy vacancies migration in Fe33Ni33Cr alloy. Interestingly, a significant increase Void of obstacle strength for void at 900K is noted only in Fe10Ni20Cr alloy because of the transformation Dislocation from void to stacking fault tetrahedra (SFT). It is found that the compress strain upon the edge dislocation Concentrated solid-solution alloys glide plane promotes the transformation from void to SFT at 900K in Fe10Ni20Cr alloy. While in Molecular dynamics Fe33Ni33Cr alloy, sluggish diffusion induced by atomic-level heterogeneity suppresses the transition from void to SFT. Consequently, Fe33Ni33Cr concentrated solid-solution alloy exhibits better irradiation hardening resistance than Fe10Ni20Cr alloy, especially at high temperature. (c) 2020 Elsevier B.V. All rights reserved. 1. Introduction Simulation is an effective method to study the evolution mechanism of material microstructure and mechanical properties [15-18]. The molecular dynamics (MD) simulation is widely used to study the atomic-scale mechanism of void hardening in traditional irradiation resistance, making them promising candidate materials in fcc materials [19-21]. The interaction of an edge dislocation with advanced nuclear reactors [1-4]. CSAs are suitable to service in the voids in Cu is investigated by MD simulation at 300K. It's reported harsh service environment, such as high temperature, high irradia- that the edge dislocation dissociates into two shockley partial distion dose and severe corrosion environment. Voids are one of main locations. With the increasing of void radius, the depinning stress of typical radiation defects in alloys and metals with face-centered cubic the trailing partial dislocation from the void increases logarithmi(fcc) structure, including austenitic stainless steels, copper (Cu), nickel cally. While the piecewise logarithmic behaviors is found for the (Ni) metals [5-8], as well as fcc CSAs [9-11]. Meanwhile, they have leading partial dislocation and the depinning stress of void with also been demonstrated to hinder the dislocation glide, and thus radius exceeding 1 nm becomes big [19]. Temperature and strain contribute to the irradiation hardening [12-14]. The mechanism of rate dependences of the critical resolved shear stress (CRSS) for interaction between a dislocation and a void has not been widely small voids are different in iron (Fe) and Cu because the partial investigated in previous studies of fcc CSAs. Therefore, it is necessary dislocations break from a void individually in Cu [21]. Modeling to study the interaction between a dislocation and a void in order to parameters have effect on the dynamics of interaction between an better understand the irradiation hardening contributed by void and edge dislocation and a void in Cu [22]. It is shown that the constant design new type CSAs with good irradiation resistance. applied strain rate loading mode is better than the constant applied strain stress in the dislocation-void interaction cases. The interaction mechanisms between the gliding dissociated edge dislocation * Corresponding author. and voids with diameter of 1 and 2nm in Ni are different. As for the leading and trailing partial dislocations detach from void with freely during MD calculation. Periodic boundary conditions are diameters of 2nm simultaneously [23]. The MD simulation results applied along the x - and y-directions in the box. The atoms in the indicate that the attraction between a dislocation and a void slows upper region B and lower region F are immobile. These rigid regions down the dislocation motion, leading to void strengthening in fcc are regularly replicated in the x and y directions. The shear strain aluminium (AI) [24]. While, the substitution of Mg atoms would deformation is applied by the incremental displacement of the increase the peierls stress and the CRSS for dislocation glide in region B in the x-direction, and the region F is fixed. The correAl5Mg alloy. Meanwhile, replacing of the Mg solute atoms sponding resolved shear stress are induced by the applied deforchanges the type of dislocation-void interaction from simultaneous mation, calculated as =Fx/AxyFx is the total force in x-direction passing of partial dislocations into the separate passing of partial originated from all atoms of the middle region A to the upper region dislocations [25]. The stacking fault energy (SFE) has an effect on B, and Axy is the xy cross-section area of the box. The size of the the interaction morphologies between a screw dislocation and middle region of the MD box is 116a,66a and 31a. And calculated spherical voids in fcc metals at 100K [26]. Previous researches have lattice constant a of Fe10Ni20Cr and Fe33Ni33Cr is about 3.52A and shown that intrinsic characteristics of different traditional mate- 3.56A, respectively. As shown in Fig. 1 b, an infinitely long and dislocation and a void. the y-direction, which has burgers vector b=1/2[110] paralleled to Until now, studies on the mechanism of void strengthening the x axis. And the dislocation is located in the center of the MD mainly focus on the fcc traditional metals. however, it remains box. unclear in fcc CSAs. The chemically disordered structures and lat- Void with its equator lying on the glide plane of dislocation is tice distortion in CSAs have been proved to lead to excellent me- introduced into the middle region of the MD box. The void with chanical properties [27,28]and irradiation resistance [2,29,30]. The diameter of 2nm is placed about 7nm away from the dislocation atomic-level heterogeneity will result in the distributions of SFE line to avoid a strong interaction with a dislocation before it glides. values at different local atomic environments in concentrated solid- According to the distance between the center of the void and the solution Ni-Fe alloys. And these variations induce the obvious dislocation, the coordinates of the center of the void can be fluctuations in dislocation segments along the dislocation line [31]. determined. All the atoms in the region within 1nm of the center of And the fluctuations in SFEs are conducive to increase the onset the void are excavated to form a void with radius of 1nm. Due to stress required for dislocation motion in Ni-Fe concentrated solid- the applied periodic boundary conditions along the x - and y-disolution alloys, as well as suppressing the formation and growth of rections in the box, the spaces of center to center between voids is defect cluster [32]. In addition, it indicates that the interaction about 41nm in the x-direction and 23nm in the y-direction. The between a vacancy and an edge dislocation is weak in Ni-Fe corresponding number density is about 9.21022m3. It is found concentrated solid-solution alloys, compared to that in pure Ni, that the number density of voids detected in austenitic stainless which is attributed to the highly heterogeneous strain energy and steel is between 1022m3 and 1023m3 under neutron irradiation at stress field around the different edge dislocation segments [33]. It is 400C to dose of less than 0.5dpa [34]. A framework of microreasonable to believe that the heterogeneity will also have effect on canonical NVE ensemble is applied in the simulation, where the the interaction of a dislocation with a void. As a promising material number of atoms (N), the volume (V) and total energy (E) of the in advance nuclear reactors, it is worthwhile to make a detailed system are conserved [35]. A comprehensive method is applied to study on the influence of heterogeneity on mechanism of void identify the stacking fault and dislocation core atoms, which constrengthening in fcc CSAs, in order to tailor their mechanical and tains potential energy analysis, common neighbor analysis, central irradiation properties. symmetry analysis and counting specific number of fcc neighbors. The purpose of this paper is to study the interaction of a 1/ The crystal is relaxed to minimize the potential energy. Strain is 2{111} edge dislocation with a void in Fe10Ni20Cr and applied at a constant rate =5107s1 to systems and the temFe33Ni33Cr concentrated solid-solution alloys with fcc structure by perature is increased from 300K to 1000K. The integration of using MD simulation method. Fe10Ni20Cr model alloy is selected Newton's equations in the MD code is performed using a constant because most austenitic stainless steels used in nuclear reactors are time step equal to 5fs at each temperature. mainly composed of 70%Fe,10%Ni and 20%Cr [34]. While Fe33Ni33Cr alloy, as a concentrated solid-solution alloys, is used to compared with the Fe10Ni20Cr alloy to investigate the influence of 3. Results and discussions bigger heterogeneity of random arrangement elements on the irradiation hardening induced by void. The impact of different 3.1. The interaction between an edge dislocation and a void at 300K temperatures and interactive geometries on void strengthening are also further explored. The mechanisms of interaction of an edge The snapshots of interaction between an edge dislocation and a dislocation with a void in these two alloys are discussed. void in Fe10Ni20Cr and Fe33Ni33Cr alloys can be seen in the Fig. 2 . The pure edge dislocations in Fe10Ni20Cr and Fe33Ni33Cr alloys both dissociate into two shockley partial dislocation with stacking 2. Method fault between them according to Eq. (1) [19]. In the present study, the models developed by Osetsky and 2a[110]6a[211]+6a[121] Bacon are used for studying the interaction of an edge dislocation and a void in the Fe10Ni20Cr and Fe33Ni33Cr alloys [21]. The The separated distance of leading and trailing partial dislocaapplied ternary Fe-Ni-Cr potential is based on the embedded tions in Fe10Ni20Cr alloy is approximate 8.5nm. The dislocation atom method (EAM) and developed by Bonny et al. [17]. The fcc shape and the distance between partial dislocations slightly fluccrystal simulation box is shown in Fig. 1, with the principal axes x,y tuate in Fe10Ni20Cr alloy, while more fluctuations in Fe33Ni33Cr and z oriented along the [110], [112] and [1111] directions. The atoms alloy. Fig. 3 shows stress-strain behaviors of an edge dislocation in regions P will interact with those from the inner region A. The interaction with 2nm void at 300K in Fe10Ni20Cr and Fe33Ni33Cr dimensions of inner region A are Lb,L and H along x,y, and z-di- alloys, respectively. It can be divided into four processes for interrections, respectively. The atoms in the inner region A can move action of the edge dislocation with the void in the two alloys. In Fig. 1. (a) Schematic of simulated crystallite; (b) Periodic cell of MD Simulation for the interaction of an edge dislocation and a void. (a) (c) (d) Fe10Ni20Cr (e) ) (g) Fe33Ni33Cr Fig. 2. Snapshots of interaction between an edge dislocation and a void in Fe10Ni20Cr alloy (a-d) and Fe33Ni33Cr alloy (e-h). The red atoms stand for the hexagonal close-packed structure atoms, and green ones are high potential energy atoms with low coordination numbers around void. (For interpretation of the references to colour in this figure legend, the reader is referred to the Web version of this article.) process I the edge dislocation starts to move in both alloys' matrix, the stacking fault energy (SFE). Therefore, the SFE of these two alcorresponding to the Fig. 2(a) and (e). In process II the leading loys are further calculated using the open-source Large-scale partial dislocation interacts with void. The snapshots of leading Atomic/Molecular Massively Parallel Simulator (LAMMPS) code And Fig. 2(c) and (g) present the snapshots of the detachment of directions, and there are 1,12 and 12 layers along these directions, leading partial one from void in both alloys. In process III the respectively. The calculated stacking fault area is determined by the trailing partial dislocation interacts with void. The snapshots for size in [011][211] plane. Due to random elemental arrangement trailing partial one detaches from void are shown in Fig. 2 (d) and near the stacking fault region, the values of SFE in these two alloys (h). In process IV the dislocation has detached from void, and are a distribution, not a single value. A number of 4000 calculations continues to glide with the stress decreasing. are performed by varying element arrangement using different With increasing of the applied strain in process I, the dislocation random seeds in the simulations. And the results of SFE distribution needs to overcome the lattice friction resistance to slip in matrix. is treated with a Gaussian function When the applied strain rises to 0.49% and the corresponding movement time of dislocation reaches to 0.50ps, the leading dislocation begins to contact with the void in Fe 10Ni20Cr alloy (as seen in Table .1). While they are 0.67% and 0.68ps in Fe33 Ni33Cr y=y0+w/2Ae2w2(xx)2 alloy, respectively. The dislocation slips the same distance and takes longer. It indicates that dislocation motion slows down in where the fitted mean value xc and standard deviation w are obFe33Ni33Cr alloy. The dislocation properties have close ties with tained. And the value of w reflects the fluctuation in SFE segments still pinned. It leads to the larger fluctuations of shape and dissociated distance of dislocation. In process II when the partial dislocations begin to contact with void, it will become bow and pinned by the void because of passage of edge dislocation sheared the void (as shown in Fig. 2(b) and (f)). Fig. 5 is the specific snapshots of the leading partial dislocation detached from the void in Fe10Ni20Cr and Fe33Ni33Cr alloys, which are corresponding to the Fig. 2(c) and (g). It can be found that the dislocation passes by the void, not climbing. It is due to larger fluctuation of SFE, although void-induced climbing might occur for other fcc metals with a high value of SFE, such as Cu and Ni [38]. In the process II and III in Fe10Ni20Cr alloy, when the applied strain reaches to 1.21% and 1.87%, the leading and trailing dislocations break away from the void, respectively. The corresponding interact time of partial dislocations with void are 0.72ps and 0.66ps. The stress peaks A and B are corresponding to the depinning stress of leading and trailing partial dislocations, which is 240 and 271MPa. As for Fe33Ni33Cr alloy, the leading and trailing dislocations break away the depinning of void at the applied strain of 1.26% and 1.67%. The corresponding interact time of partial dislocations with void are 0.59ps and 0.41ps. The maximum stress peaks C and D are 244 and 255MPa. It can be seen that the void depinning resistance for trailing dislocation is bigger than that for leading dislocation. And the maximum depinning stress of dislocation is taken as CRSS. As for Fe10Ni20Cr alloy, the maximum stress of leading dislocation is significantly less than that of trailing dislocation. As the leading dislocation bows and the trailing dislocation attaches to the void, the separation distance between them decreases (as shown in Fig. 5(a)). As a result, a significant repulsive force occurs between the two partial dislocations. The trailing dislocation can push the leading one forward and help it depinning from the void. While, the trailing dislocation gets rid of the pinning of void without any help. leading to the higher maximum stress. In Fe33 Ni33Cr alloy, the leading and trailing partial dislocations intersect with the void almost separately. When the leading partial dislocation detaches from the void, the trailing partial one has not contacted with the void. The separation distance between dislocation partial dislocation is bigger than that in Fe10Ni20Cr alloy (as shown in Fig. 5(b)). It Fig. 3. Stress-strain curves of an edge dislocation interaction with 2nm void at 300K : makes the repulsive force between the leading and trailing dislo(a) in Fe10Ni20Cr alloy: (b) in Fe33Ni33Cr alloy. Two circles indicate two partial cations become weak. The partial dislocations interact with void as dislocation breaking away from the void. an isolated one, hardly affected by another one in Fe33 Ni33Cr alloy. Hence, the maximum stress of peaks does not vary greatly in distribution. As shown in Fig. 4, the xc and w of SFE for Fe33Ni33Cr Fe33Ni33Cr alloy. It is interesting to find that the interaction time of is all higher than that of Fe10Ni20Cr alloy. It is consistent with the the dislocation with the in simulation results reported by Zhao et al. that is, decreasing of Ni CRSS is a little smaller, compared to Fe10Ni20Cr alloy. It's suggested and Cr concentrations will lead to the low SFEs in FeNiCr system that the void strengthening is slightly weak in Fe33Ni33Cr alloy. alloys [32]. The heterogeneity of random arrangement of elements According to previous simulation results, a large fraction of barriers in Fe33Ni33Cr alloy is much bigger than that in Fe10Ni20Cr alloy, of vacancy migration in NiCoCr is lower than those in pure Ni [39]. which increases the fluctuations of SFE. The larger fluctuations of The vacancy migration is more easy in Fe50Ni concentrated solidSFE at different local atom environment have important effect of solution alloys, compared to Fe20Ni alloys [40]. The migration enthe movement of dislocation. it would increase the threshold stress ergies for Fe, Ni and Cr vacancies in Fe10Ni20Cr and Fe33Ni33Cr for dislocation motion and slow the dislocation motion [31,32,37]. alloys are calculated using of MD simulation, respectively. The Due to the larger fluctuation of SFE in Fe33Ni33Cr alloy, the partial whole migration energies of vacancies, are shown in Fig. 6. It is segments of dislocation can move forward, along with other found the distribution of migration energies for vacancies in Fig. 6. Distribution of migration energies for vacancies in Fe10Ni20Cr and Fe33Ni33Cr alloys. 3.2. The temperature effect on the void strengthening Fig. 5. Snapshots of the leading partial dislocation detached from the void in Fe10Ni20Cr alloy (a) and Fe33Ni33Cr alloy (b). Fig. 7(a) and (b) present the applied stress as functions of the applied strain in Fe10Ni20Cr and Fe33Ni33Cr alloys for void with diameter of 2nm at temperature of 300K1000K. And Fig. 7(c) shows the trend of the CRSS of void with the increasing of tem- Fe33Ni33Cr alloy is broaden, compared to Fe10Ni20Cr alloy. perature in both alloys. The CRSS of Fe33Ni33Cr alloy is smaller Meanwhile, the peak of migration energies distribution for va- than that of 10Ni20Cr alloy in the investigated temperature cancies in Fe33Ni33Cr alloys shifts to lower energy region than that range. The CRSS decreases with increasing of temperature in both in Fe10Ni20Cr alloy. The results indicate that the migration of va- Fe33Ni33Cr and Fe10Ni20Cr alloys, except for a remarkable incancies in Fe33Ni33Cr alloy will be faster than that in Fe10Ni20Cr crease of maximum shear stress at 900K in Fe10Ni20Cr alloy. The alloy. Therefore, dislocation is easy to pass through the void by decreasing of CRSS with the increasing of temperature is because exchange of vacancies on the surface of void in Fe33Ni33Cr alloy the atom thermal agitation at high temperature partly promote the than in Fe10Ni20Cr alloy. In other words, the pinning strength of motion of dislocation [41]. Fig. 8 presents snapshots of departure of void for dislocation glide is weaker in Fe33Ni33Cr alloy than in trailing dislocation from void in Fe10Ni20Cr and Fe33Ni33Cr alloys Fe10Ni20Cr alloy. at 900K and 1000K. Interestingly, it is found that the void (a (b (c Fig. 8. Snapshots of departure of the dislocation from the void: (a) in Fe10Ni20Cr alloy at 900K; (b) in Fe10Ni20Cr alloy at 1000K; (c) in Fe33Ni33Cr alloy at 900K; (d) in Fe33Ni33Cr alloy at 1000K. The red atoms stand for the hexagonal close-packed structure atoms, green ones are high potential energy atoms with low coordination numbers around void, and blue ones are low coordination number fcc atoms. (For interpretation of the references to colour in this figure legend, the reader is referred to the Web version of this article.) Fig. 9. Dependence of microstructure evolution with applied strain in the sample at 900K in Fe10Ni20Cr alloy: (a-e) the sample containing a dislocation and a void; (f-j) the sample containing only a void. H=0.25 is the smallest, standing for the biggest pinning strength of void. As for model H=1, the void shows the weakest pinning strength for the dislocation gliding. There is a completely different dependence of CRSS on the interacting sites in Fe10Ni20Cr alloy, as shown in the Fig. 10(b). CRSS declines approximately linearly with the increasing of H. (D) According to the Fig. 12, while the dislocation glides tangentially from the bottom of the void, the transition of void into SFT is more thoroughly than other modes. The number of activated equivalents \{111\} glide planes is increased and two intercrossed SFTs are formed, denoted as SFT1 and SFT2. The small SFTs grow by expensing of their ledges, and they connect together by the common vertices as B,C and D. With the increasing of the H, the size of formed SFT is becoming smaller. And only the SFT2 emerges in the model H=0.5 and 0.75 . And there is no transition of void into SFT for H=1. It is known that the upper half of the edge dislocation gliding plane is subjected to compressive stress, while the lower half is subjected to tensile stress. The compressive stress can promote the transition of void into SFT demonstrated by previous MD simulations results [43]. The vacancy on the void surface is to be quite mobile at moderate temperature. It is easy to execute a hop around void, and corresponding atoms in matrix would migrate to the surface of void to triggering the formation of the SDs in Fe10Ni20Cr alloy at 900K. When dislocation contacts with the void, more atoms near the stacking fault of edge dislocation migrate to Fig. 10. (a) Schematic of the configurations studied for voids with diameter D. H is the the SDs under compressive stress, followed with the appearance of distance of the bottom of the void and the dislocation glide plane; (b) the critical the stress-interacting sites dependence for 2nm void in Fe 10Ni20Cr and Fe33Ni33Cr alloys SFs and SJs. Eventually, the SFT is formed. In the temperature range at 900K. Fig. 11. Critical snapshots of the edge dislocation break away the depinning of 2nm void with different interactive geometries at 900n in Fe33Ni33Cr alloy. Fig. 12. Critical snapshots of the edge dislocation break away the depinning of 2nm void with different interactive geometries at 900K in Fe10Ni20Cr alloy. of 300K800K, there is no transformation of void into SFT in 4. Conclusion Fe 10Ni20Cr alloy. It is possible that the void is kinetically trapped as void and hardly to transform into SFT. Increasing the temperature In this paper, we investigate the interaction of a 1/2 I11\} would promote the transformation [44]. Therefore, only under the edge dislocation with a void in Fe10Ni20Cr and Fe33Ni33Cr combined action of compressive stress and sufficiently high tem- concentrated solid-solution alloys by using molecular dynamics perature, the SJs can grow up and SFT can be formed in Fe10Ni20Cr simulation method. The following conclusions are obtained: alloy. The early result has reported that the interstitials migration 1. The edge dislocation dissociates into two shockley partial disenergies have a distributed feature and shift to the high energy locations with stacking fault in both alloys. Due to big region. It makes interstitial diffusion become slower in Fe-Ni sys- fluctuation of stacking fault energy, the dislocation motion betem concentrated solid-solution alloys with high atomic hetero- comes more difficult in Fe33Ni33Cr alloy than that in geneity, compared to the Ni metal [45]. The atomic heterogeneity in Fe10Ni20Cr alloy. Fe33Ni33Cr alloy is bigger than Fe10Ni20Cr alloy. Hence, atoms 2. The depinning stress of void for dislocation glide in Fe33Ni33Cr migration by swapping atoms is more difficult in Fe33Ni33Cr alloy, alloy is a little bit lower than that of Fe10Ni20Cr alloy at temleading to the SDs, SFs or SJs hardly formed on the surface of void. perature of 300K800K, because vacancies in the void are more And the transformation from void into SFT is suppressed in prone to migration in Fe33Ni33Cr alloy. Fe33Ni33Cr alloy. Therefore, the CRSS of the dislocation gliding 3. Void can transform into SFT and lead to a significant increase of through the void is lower in Fe33Ni33Cr alloy than that of obstacle strength for void in Fe10Ni20Cr alloy under the comFe10Ni20Cr alloy, which demonstrates that the Fe33Ni33 Cr alloy bined action of compressive stress and sufficiently high temhas better resistance to irradiation hardening than Fe10Ni20Cr perature, such as 900K. However, sluggish diffusion induced by alloy, especially at higher temperature. atomic-level heterogeneity makes atoms migrate more slowly, and inhibits the transform from void into SFT in Fe33Ni33Cr Article history: The interactions of a 1/2{111} edge dislocation with a void in Fe10Ni20Cr and Fe33Ni33Cr Received 3 August 2020 concentrated solid-solution alloys are investigated by using molecular dynamics simulation method. The Received in revised form edge dislocation dissociates into two shockley partial dislocations with stacking fault in both alloys. 28 September 2020 Compared to the Fe10Ni20Cr alloy, the dislocation motion becomes difficult in Fe33Ni33Cr alloy due to Accepted 11 October 2020 Available online 15 October 2020 the big fluctuation of stacking fault energy. The obstacle strength for a void with diameter of 2 nm in Fe33Ni33Cr alloy is slightly weaker than that in Fe10Ni20Cr alloy at temperature range from 300K to Keywords: 800K. It is attributed to easy vacancies migration in Fe33Ni33Cr alloy. Interestingly, a significant increase Void of obstacle strength for void at 900K is noted only in Fe10Ni20Cr alloy because of the transformation Dislocation from void to stacking fault tetrahedra (SFT). It is found that the compress strain upon the edge dislocation Concentrated solid-solution alloys glide plane promotes the transformation from void to SFT at 900K in Fe10Ni20Cr alloy. While in Molecular dynamics Fe33Ni33Cr alloy, sluggish diffusion induced by atomic-level heterogeneity suppresses the transition from void to SFT. Consequently, Fe33Ni33Cr concentrated solid-solution alloy exhibits better irradiation hardening resistance than Fe10Ni20Cr alloy, especially at high temperature. (c) 2020 Elsevier B.V. All rights reserved. 1. Introduction Simulation is an effective method to study the evolution mechanism of material microstructure and mechanical properties [15-18]. The molecular dynamics (MD) simulation is widely used to study the atomic-scale mechanism of void hardening in traditional irradiation resistance, making them promising candidate materials in fcc materials [19-21]. The interaction of an edge dislocation with advanced nuclear reactors [1-4]. CSAs are suitable to service in the voids in Cu is investigated by MD simulation at 300K. It's reported harsh service environment, such as high temperature, high irradia- that the edge dislocation dissociates into two shockley partial distion dose and severe corrosion environment. Voids are one of main locations. With the increasing of void radius, the depinning stress of typical radiation defects in alloys and metals with face-centered cubic the trailing partial dislocation from the void increases logarithmi(fcc) structure, including austenitic stainless steels, copper (Cu), nickel cally. While the piecewise logarithmic behaviors is found for the (Ni) metals [5-8], as well as fcc CSAs [9-11]. Meanwhile, they have leading partial dislocation and the depinning stress of void with also been demonstrated to hinder the dislocation glide, and thus radius exceeding 1 nm becomes big [19]. Temperature and strain contribute to the irradiation hardening [12-14]. The mechanism of rate dependences of the critical resolved shear stress (CRSS) for interaction between a dislocation and a void has not been widely small voids are different in iron (Fe) and Cu because the partial investigated in previous studies of fcc CSAs. Therefore, it is necessary dislocations break from a void individually in Cu [21]. Modeling to study the interaction between a dislocation and a void in order to parameters have effect on the dynamics of interaction between an better understand the irradiation hardening contributed by void and edge dislocation and a void in Cu [22]. It is shown that the constant design new type CSAs with good irradiation resistance. applied strain rate loading mode is better than the constant applied strain stress in the dislocation-void interaction cases. The interaction mechanisms between the gliding dissociated edge dislocation * Corresponding author. and voids with diameter of 1 and 2nm in Ni are different. As for the leading and trailing partial dislocations detach from void with freely during MD calculation. Periodic boundary conditions are diameters of 2nm simultaneously [23]. The MD simulation results applied along the x - and y-directions in the box. The atoms in the indicate that the attraction between a dislocation and a void slows upper region B and lower region F are immobile. These rigid regions down the dislocation motion, leading to void strengthening in fcc are regularly replicated in the x and y directions. The shear strain aluminium (AI) [24]. While, the substitution of Mg atoms would deformation is applied by the incremental displacement of the increase the peierls stress and the CRSS for dislocation glide in region B in the x-direction, and the region F is fixed. The correAl5Mg alloy. Meanwhile, replacing of the Mg solute atoms sponding resolved shear stress are induced by the applied deforchanges the type of dislocation-void interaction from simultaneous mation, calculated as =Fx/AxyFx is the total force in x-direction passing of partial dislocations into the separate passing of partial originated from all atoms of the middle region A to the upper region dislocations [25]. The stacking fault energy (SFE) has an effect on B, and Axy is the xy cross-section area of the box. The size of the the interaction morphologies between a screw dislocation and middle region of the MD box is 116a,66a and 31a. And calculated spherical voids in fcc metals at 100K [26]. Previous researches have lattice constant a of Fe10Ni20Cr and Fe33Ni33Cr is about 3.52A and shown that intrinsic characteristics of different traditional mate- 3.56A, respectively. As shown in Fig. 1 b, an infinitely long and dislocation and a void. the y-direction, which has burgers vector b=1/2[110] paralleled to Until now, studies on the mechanism of void strengthening the x axis. And the dislocation is located in the center of the MD mainly focus on the fcc traditional metals. however, it remains box. unclear in fcc CSAs. The chemically disordered structures and lat- Void with its equator lying on the glide plane of dislocation is tice distortion in CSAs have been proved to lead to excellent me- introduced into the middle region of the MD box. The void with chanical properties [27,28]and irradiation resistance [2,29,30]. The diameter of 2nm is placed about 7nm away from the dislocation atomic-level heterogeneity will result in the distributions of SFE line to avoid a strong interaction with a dislocation before it glides. values at different local atomic environments in concentrated solid- According to the distance between the center of the void and the solution Ni-Fe alloys. And these variations induce the obvious dislocation, the coordinates of the center of the void can be fluctuations in dislocation segments along the dislocation line [31]. determined. All the atoms in the region within 1nm of the center of And the fluctuations in SFEs are conducive to increase the onset the void are excavated to form a void with radius of 1nm. Due to stress required for dislocation motion in Ni-Fe concentrated solid- the applied periodic boundary conditions along the x - and y-disolution alloys, as well as suppressing the formation and growth of rections in the box, the spaces of center to center between voids is defect cluster [32]. In addition, it indicates that the interaction about 41nm in the x-direction and 23nm in the y-direction. The between a vacancy and an edge dislocation is weak in Ni-Fe corresponding number density is about 9.21022m3. It is found concentrated solid-solution alloys, compared to that in pure Ni, that the number density of voids detected in austenitic stainless which is attributed to the highly heterogeneous strain energy and steel is between 1022m3 and 1023m3 under neutron irradiation at stress field around the different edge dislocation segments [33]. It is 400C to dose of less than 0.5dpa [34]. A framework of microreasonable to believe that the heterogeneity will also have effect on canonical NVE ensemble is applied in the simulation, where the the interaction of a dislocation with a void. As a promising material number of atoms (N), the volume (V) and total energy (E) of the in advance nuclear reactors, it is worthwhile to make a detailed system are conserved [35]. A comprehensive method is applied to study on the influence of heterogeneity on mechanism of void identify the stacking fault and dislocation core atoms, which constrengthening in fcc CSAs, in order to tailor their mechanical and tains potential energy analysis, common neighbor analysis, central irradiation properties. symmetry analysis and counting specific number of fcc neighbors. The purpose of this paper is to study the interaction of a 1/ The crystal is relaxed to minimize the potential energy. Strain is 2{111} edge dislocation with a void in Fe10Ni20Cr and applied at a constant rate =5107s1 to systems and the temFe33Ni33Cr concentrated solid-solution alloys with fcc structure by perature is increased from 300K to 1000K. The integration of using MD simulation method. Fe10Ni20Cr model alloy is selected Newton's equations in the MD code is performed using a constant because most austenitic stainless steels used in nuclear reactors are time step equal to 5fs at each temperature. mainly composed of 70%Fe,10%Ni and 20%Cr [34]. While Fe33Ni33Cr alloy, as a concentrated solid-solution alloys, is used to compared with the Fe10Ni20Cr alloy to investigate the influence of 3. Results and discussions bigger heterogeneity of random arrangement elements on the irradiation hardening induced by void. The impact of different 3.1. The interaction between an edge dislocation and a void at 300K temperatures and interactive geometries on void strengthening are also further explored. The mechanisms of interaction of an edge The snapshots of interaction between an edge dislocation and a dislocation with a void in these two alloys are discussed. void in Fe10Ni20Cr and Fe33Ni33Cr alloys can be seen in the Fig. 2 . The pure edge dislocations in Fe10Ni20Cr and Fe33Ni33Cr alloys both dissociate into two shockley partial dislocation with stacking 2. Method fault between them according to Eq. (1) [19]. In the present study, the models developed by Osetsky and 2a[110]6a[211]+6a[121] Bacon are used for studying the interaction of an edge dislocation and a void in the Fe10Ni20Cr and Fe33Ni33Cr alloys [21]. The The separated distance of leading and trailing partial dislocaapplied ternary Fe-Ni-Cr potential is based on the embedded tions in Fe10Ni20Cr alloy is approximate 8.5nm. The dislocation atom method (EAM) and developed by Bonny et al. [17]. The fcc shape and the distance between partial dislocations slightly fluccrystal simulation box is shown in Fig. 1, with the principal axes x,y tuate in Fe10Ni20Cr alloy, while more fluctuations in Fe33Ni33Cr and z oriented along the [110], [112] and [1111] directions. The atoms alloy. Fig. 3 shows stress-strain behaviors of an edge dislocation in regions P will interact with those from the inner region A. The interaction with 2nm void at 300K in Fe10Ni20Cr and Fe33Ni33Cr dimensions of inner region A are Lb,L and H along x,y, and z-di- alloys, respectively. It can be divided into four processes for interrections, respectively. The atoms in the inner region A can move action of the edge dislocation with the void in the two alloys. In Fig. 1. (a) Schematic of simulated crystallite; (b) Periodic cell of MD Simulation for the interaction of an edge dislocation and a void. (a) (c) (d) Fe10Ni20Cr (e) ) (g) Fe33Ni33Cr Fig. 2. Snapshots of interaction between an edge dislocation and a void in Fe10Ni20Cr alloy (a-d) and Fe33Ni33Cr alloy (e-h). The red atoms stand for the hexagonal close-packed structure atoms, and green ones are high potential energy atoms with low coordination numbers around void. (For interpretation of the references to colour in this figure legend, the reader is referred to the Web version of this article.) process I the edge dislocation starts to move in both alloys' matrix, the stacking fault energy (SFE). Therefore, the SFE of these two alcorresponding to the Fig. 2(a) and (e). In process II the leading loys are further calculated using the open-source Large-scale partial dislocation interacts with void. The snapshots of leading Atomic/Molecular Massively Parallel Simulator (LAMMPS) code And Fig. 2(c) and (g) present the snapshots of the detachment of directions, and there are 1,12 and 12 layers along these directions, leading partial one from void in both alloys. In process III the respectively. The calculated stacking fault area is determined by the trailing partial dislocation interacts with void. The snapshots for size in [011][211] plane. Due to random elemental arrangement trailing partial one detaches from void are shown in Fig. 2 (d) and near the stacking fault region, the values of SFE in these two alloys (h). In process IV the dislocation has detached from void, and are a distribution, not a single value. A number of 4000 calculations continues to glide with the stress decreasing. are performed by varying element arrangement using different With increasing of the applied strain in process I, the dislocation random seeds in the simulations. And the results of SFE distribution needs to overcome the lattice friction resistance to slip in matrix. is treated with a Gaussian function When the applied strain rises to 0.49% and the corresponding movement time of dislocation reaches to 0.50ps, the leading dislocation begins to contact with the void in Fe 10Ni20Cr alloy (as seen in Table .1). While they are 0.67% and 0.68ps in Fe33 Ni33Cr y=y0+w/2Ae2w2(xx)2 alloy, respectively. The dislocation slips the same distance and takes longer. It indicates that dislocation motion slows down in where the fitted mean value xc and standard deviation w are obFe33Ni33Cr alloy. The dislocation properties have close ties with tained. And the value of w reflects the fluctuation in SFE segments still pinned. It leads to the larger fluctuations of shape and dissociated distance of dislocation. In process II when the partial dislocations begin to contact with void, it will become bow and pinned by the void because of passage of edge dislocation sheared the void (as shown in Fig. 2(b) and (f)). Fig. 5 is the specific snapshots of the leading partial dislocation detached from the void in Fe10Ni20Cr and Fe33Ni33Cr alloys, which are corresponding to the Fig. 2(c) and (g). It can be found that the dislocation passes by the void, not climbing. It is due to larger fluctuation of SFE, although void-induced climbing might occur for other fcc metals with a high value of SFE, such as Cu and Ni [38]. In the process II and III in Fe10Ni20Cr alloy, when the applied strain reaches to 1.21% and 1.87%, the leading and trailing dislocations break away from the void, respectively. The corresponding interact time of partial dislocations with void are 0.72ps and 0.66ps. The stress peaks A and B are corresponding to the depinning stress of leading and trailing partial dislocations, which is 240 and 271MPa. As for Fe33Ni33Cr alloy, the leading and trailing dislocations break away the depinning of void at the applied strain of 1.26% and 1.67%. The corresponding interact time of partial dislocations with void are 0.59ps and 0.41ps. The maximum stress peaks C and D are 244 and 255MPa. It can be seen that the void depinning resistance for trailing dislocation is bigger than that for leading dislocation. And the maximum depinning stress of dislocation is taken as CRSS. As for Fe10Ni20Cr alloy, the maximum stress of leading dislocation is significantly less than that of trailing dislocation. As the leading dislocation bows and the trailing dislocation attaches to the void, the separation distance between them decreases (as shown in Fig. 5(a)). As a result, a significant repulsive force occurs between the two partial dislocations. The trailing dislocation can push the leading one forward and help it depinning from the void. While, the trailing dislocation gets rid of the pinning of void without any help. leading to the higher maximum stress. In Fe33 Ni33Cr alloy, the leading and trailing partial dislocations intersect with the void almost separately. When the leading partial dislocation detaches from the void, the trailing partial one has not contacted with the void. The separation distance between dislocation partial dislocation is bigger than that in Fe10Ni20Cr alloy (as shown in Fig. 5(b)). It Fig. 3. Stress-strain curves of an edge dislocation interaction with 2nm void at 300K : makes the repulsive force between the leading and trailing dislo(a) in Fe10Ni20Cr alloy: (b) in Fe33Ni33Cr alloy. Two circles indicate two partial cations become weak. The partial dislocations interact with void as dislocation breaking away from the void. an isolated one, hardly affected by another one in Fe33 Ni33Cr alloy. Hence, the maximum stress of peaks does not vary greatly in distribution. As shown in Fig. 4, the xc and w of SFE for Fe33Ni33Cr Fe33Ni33Cr alloy. It is interesting to find that the interaction time of is all higher than that of Fe10Ni20Cr alloy. It is consistent with the the dislocation with the in simulation results reported by Zhao et al. that is, decreasing of Ni CRSS is a little smaller, compared to Fe10Ni20Cr alloy. It's suggested and Cr concentrations will lead to the low SFEs in FeNiCr system that the void strengthening is slightly weak in Fe33Ni33Cr alloy. alloys [32]. The heterogeneity of random arrangement of elements According to previous simulation results, a large fraction of barriers in Fe33Ni33Cr alloy is much bigger than that in Fe10Ni20Cr alloy, of vacancy migration in NiCoCr is lower than those in pure Ni [39]. which increases the fluctuations of SFE. The larger fluctuations of The vacancy migration is more easy in Fe50Ni concentrated solidSFE at different local atom environment have important effect of solution alloys, compared to Fe20Ni alloys [40]. The migration enthe movement of dislocation. it would increase the threshold stress ergies for Fe, Ni and Cr vacancies in Fe10Ni20Cr and Fe33Ni33Cr for dislocation motion and slow the dislocation motion [31,32,37]. alloys are calculated using of MD simulation, respectively. The Due to the larger fluctuation of SFE in Fe33Ni33Cr alloy, the partial whole migration energies of vacancies, are shown in Fig. 6. It is segments of dislocation can move forward, along with other found the distribution of migration energies for vacancies in Fig. 6. Distribution of migration energies for vacancies in Fe10Ni20Cr and Fe33Ni33Cr alloys. 3.2. The temperature effect on the void strengthening Fig. 5. Snapshots of the leading partial dislocation detached from the void in Fe10Ni20Cr alloy (a) and Fe33Ni33Cr alloy (b). Fig. 7(a) and (b) present the applied stress as functions of the applied strain in Fe10Ni20Cr and Fe33Ni33Cr alloys for void with diameter of 2nm at temperature of 300K1000K. And Fig. 7(c) shows the trend of the CRSS of void with the increasing of tem- Fe33Ni33Cr alloy is broaden, compared to Fe10Ni20Cr alloy. perature in both alloys. The CRSS of Fe33Ni33Cr alloy is smaller Meanwhile, the peak of migration energies distribution for va- than that of 10Ni20Cr alloy in the investigated temperature cancies in Fe33Ni33Cr alloys shifts to lower energy region than that range. The CRSS decreases with increasing of temperature in both in Fe10Ni20Cr alloy. The results indicate that the migration of va- Fe33Ni33Cr and Fe10Ni20Cr alloys, except for a remarkable incancies in Fe33Ni33Cr alloy will be faster than that in Fe10Ni20Cr crease of maximum shear stress at 900K in Fe10Ni20Cr alloy. The alloy. Therefore, dislocation is easy to pass through the void by decreasing of CRSS with the increasing of temperature is because exchange of vacancies on the surface of void in Fe33Ni33Cr alloy the atom thermal agitation at high temperature partly promote the than in Fe10Ni20Cr alloy. In other words, the pinning strength of motion of dislocation [41]. Fig. 8 presents snapshots of departure of void for dislocation glide is weaker in Fe33Ni33Cr alloy than in trailing dislocation from void in Fe10Ni20Cr and Fe33Ni33Cr alloys Fe10Ni20Cr alloy. at 900K and 1000K. Interestingly, it is found that the void (a (b (c Fig. 8. Snapshots of departure of the dislocation from the void: (a) in Fe10Ni20Cr alloy at 900K; (b) in Fe10Ni20Cr alloy at 1000K; (c) in Fe33Ni33Cr alloy at 900K; (d) in Fe33Ni33Cr alloy at 1000K. The red atoms stand for the hexagonal close-packed structure atoms, green ones are high potential energy atoms with low coordination numbers around void, and blue ones are low coordination number fcc atoms. (For interpretation of the references to colour in this figure legend, the reader is referred to the Web version of this article.) Fig. 9. Dependence of microstructure evolution with applied strain in the sample at 900K in Fe10Ni20Cr alloy: (a-e) the sample containing a dislocation and a void; (f-j) the sample containing only a void. H=0.25 is the smallest, standing for the biggest pinning strength of void. As for model H=1, the void shows the weakest pinning strength for the dislocation gliding. There is a completely different dependence of CRSS on the interacting sites in Fe10Ni20Cr alloy, as shown in the Fig. 10(b). CRSS declines approximately linearly with the increasing of H. (D) According to the Fig. 12, while the dislocation glides tangentially from the bottom of the void, the transition of void into SFT is more thoroughly than other modes. The number of activated equivalents \{111\} glide planes is increased and two intercrossed SFTs are formed, denoted as SFT1 and SFT2. The small SFTs grow by expensing of their ledges, and they connect together by the common vertices as B,C and D. With the increasing of the H, the size of formed SFT is becoming smaller. And only the SFT2 emerges in the model H=0.5 and 0.75 . And there is no transition of void into SFT for H=1. It is known that the upper half of the edge dislocation gliding plane is subjected to compressive stress, while the lower half is subjected to tensile stress. The compressive stress can promote the transition of void into SFT demonstrated by previous MD simulations results [43]. The vacancy on the void surface is to be quite mobile at moderate temperature. It is easy to execute a hop around void, and corresponding atoms in matrix would migrate to the surface of void to triggering the formation of the SDs in Fe10Ni20Cr alloy at 900K. When dislocation contacts with the void, more atoms near the stacking fault of edge dislocation migrate to Fig. 10. (a) Schematic of the configurations studied for voids with diameter D. H is the the SDs under compressive stress, followed with the appearance of distance of the bottom of the void and the dislocation glide plane; (b) the critical the stress-interacting sites dependence for 2nm void in Fe 10Ni20Cr and Fe33Ni33Cr alloys SFs and SJs. Eventually, the SFT is formed. In the temperature range at 900K. Fig. 11. Critical snapshots of the edge dislocation break away the depinning of 2nm void with different interactive geometries at 900n in Fe33Ni33Cr alloy. Fig. 12. Critical snapshots of the edge dislocation break away the depinning of 2nm void with different interactive geometries at 900K in Fe10Ni20Cr alloy. of 300K800K, there is no transformation of void into SFT in 4. Conclusion Fe 10Ni20Cr alloy. It is possible that the void is kinetically trapped as void and hardly to transform into SFT. Increasing the temperature In this paper, we investigate the interaction of a 1/2 I11\} would promote the transformation [44]. Therefore, only under the edge dislocation with a void in Fe10Ni20Cr and Fe33Ni33Cr combined action of compressive stress and sufficiently high tem- concentrated solid-solution alloys by using molecular dynamics perature, the SJs can grow up and SFT can be formed in Fe10Ni20Cr simulation method. The following conclusions are obtained: alloy. The early result has reported that the interstitials migration 1. The edge dislocation dissociates into two shockley partial disenergies have a distributed feature and shift to the high energy locations with stacking fault in both alloys. Due to big region. It makes interstitial diffusion become slower in Fe-Ni sys- fluctuation of stacking fault energy, the dislocation motion betem concentrated solid-solution alloys with high atomic hetero- comes more difficult in Fe33Ni33Cr alloy than that in geneity, compared to the Ni metal [45]. The atomic heterogeneity in Fe10Ni20Cr alloy. Fe33Ni33Cr alloy is bigger than Fe10Ni20Cr alloy. Hence, atoms 2. The depinning stress of void for dislocation glide in Fe33Ni33Cr migration by swapping atoms is more difficult in Fe33Ni33Cr alloy, alloy is a little bit lower than that of Fe10Ni20Cr alloy at temleading to the SDs, SFs or SJs hardly formed on the surface of void. perature of 300K800K, because vacancies in the void are more And the transformation from void into SFT is suppressed in prone to migration in Fe33Ni33Cr alloy. Fe33Ni33Cr alloy. Therefore, the CRSS of the dislocation gliding 3. Void can transform into SFT and lead to a significant increase of through the void is lower in Fe33Ni33Cr alloy than that of obstacle strength for void in Fe10Ni20Cr alloy under the comFe10Ni20Cr alloy, which demonstrates that the Fe33Ni33 Cr alloy bined action of compressive stress and sufficiently high temhas better resistance to irradiation hardening than Fe10Ni20Cr perature, such as 900K. However, sluggish diffusion induced by alloy, especially at higher temperature. atomic-level heterogeneity makes atoms migrate more slowly, and inhibits the transform from void into SFT in Fe33Ni33Cr