need the answer for 34 And 34e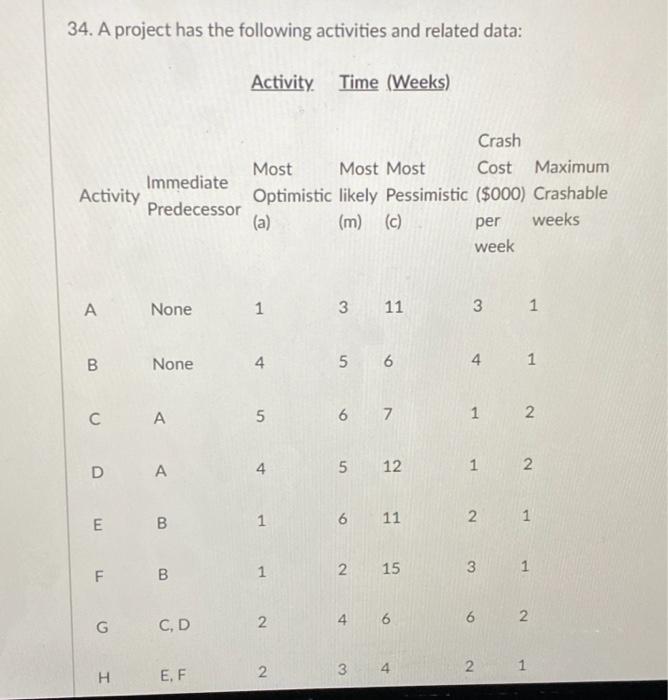

34. A project has the following activities and related data: Activity. Time (Weeks) Immediate Activity Predecessor Crash Most Most Most Cost Maximum Optimistic likely Pessimistic ($000) Crashable (a) (m) (C) per weeks week A None 1 3 11 3 1 00 None 4 5 6 4 1 5 6 7 1 2 D 4 5 12 1 2 1 E B 6 11 2 1 B 1 2 15 F 1 3 2 4 6 6 G CD 2 3 4 2 1 2 H EF G CD 2 4 6 6 N H EF 2 3 3 4 4 2 1 34a. (20 points) Compute the Expected Value E(t) and Variance V(t) for all activities. (5 points deducted for any error). Activity A B C D E F G H Et) weeks Vt) weeks 346. (15 points) There are three critical paths: ACG, ADG, and BEH, all with expected project completion time E(T)=14 weeks. Compute the variance of project completion time for each path (5 points deducted for any error) V(ACG) = V(ADG) - V(BEH) = 34c.(10 points) Assume that the project completion time T is normally distributed with mean E(T)=14 weeks, and variance V(T) approximated by the maximum of the variances of the three individual critical paths. Determine the time X in weeks for which there is a 40% probability that the project can be completed on or before X. Please show details for full credits, 34d. (40 points) List all alternatives and the respective costs for shortening the project by one week and identify the best alternative that has the minimum cost (5 points deducted for each missing or incorrect alternative). Hint: There are 8 alternatives. Alternative Cost The best alternative is 34e. (20 points) For activity i, let Xi be the Earliest Finishing time, and Yi be the number of weeks shortened. Formulate the linear program for minimizing the cost for shortening the project by one week (5 points deducted for any missing part of the formulation.) 34. A project has the following activities and related data: Activity. Time (Weeks) Immediate Activity Predecessor Crash Most Most Most Cost Maximum Optimistic likely Pessimistic ($000) Crashable (a) (m) (C) per weeks week A None 1 3 11 3 1 00 None 4 5 6 4 1 5 6 7 1 2 D 4 5 12 1 2 1 E B 6 11 2 1 B 1 2 15 F 1 3 2 4 6 6 G CD 2 3 4 2 1 2 H EF G CD 2 4 6 6 N H EF 2 3 3 4 4 2 1 34a. (20 points) Compute the Expected Value E(t) and Variance V(t) for all activities. (5 points deducted for any error). Activity A B C D E F G H Et) weeks Vt) weeks 346. (15 points) There are three critical paths: ACG, ADG, and BEH, all with expected project completion time E(T)=14 weeks. Compute the variance of project completion time for each path (5 points deducted for any error) V(ACG) = V(ADG) - V(BEH) = 34c.(10 points) Assume that the project completion time T is normally distributed with mean E(T)=14 weeks, and variance V(T) approximated by the maximum of the variances of the three individual critical paths. Determine the time X in weeks for which there is a 40% probability that the project can be completed on or before X. Please show details for full credits, 34d. (40 points) List all alternatives and the respective costs for shortening the project by one week and identify the best alternative that has the minimum cost (5 points deducted for each missing or incorrect alternative). Hint: There are 8 alternatives. Alternative Cost The best alternative is 34e. (20 points) For activity i, let Xi be the Earliest Finishing time, and Yi be the number of weeks shortened. Formulate the linear program for minimizing the cost for shortening the project by one week (5 points deducted for any missing part of the formulation.)