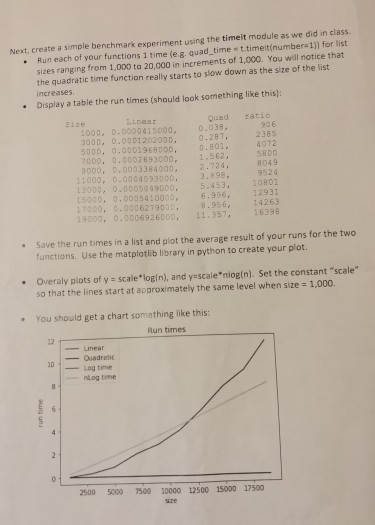
Next, create a simple benchmark experiment using the timeit module as we did in class. Run each of your functions 1 time (e.g. quad_timest timeit(number 1)) for list sizes ranging from 1,000 to 20,000 in increments of 1,000. You will notice that the quadratic time function really starts to slow down as the size of the list Increases Display a table the run times (should look something like this: ratio 906 Size Tinear 3000, 0.00000 15000 3000, 0.0001202000. 5000, 0.000196000, 7000, 0.0002693000, 5000, 0.00033840 , 11000, 0.0004093000. 3000, 0.0005009000, 30. 1.0005410000 170000.0006279000 19.000 0.0006926000, Quad 0.038. 0.287, 0.001 1.562, 2.124, 4072 5800 8349 9524 10801 12931 14263 16398 5.453, 6.996, 9.956, 11.357, Save the run times in a list and plot the average result of your runs for the two functions. Use the matplatlib library in python to create your plot. Overaly plots of y = scale*login), and yescaleniogin). Set the constant "scale" so that the lines start at approximately the same level when size = 1.000. You should get a chart something like this: Run times - Linear Quadratic nog time run time 2500 5000 7500 10000 12500 15000 17500 Topic: Algorithm Analysis 1. [40 points] Minimum in list algorithms - benchmark and plot Write two Python functions to find the minimum number in a list. The functions should take a random list of integers from 1 to 1000. The lists can be of size ranging from 1,000 to 20,000 integers, in increments of 2,000. The functions should return the minimum number in the list. The first function, f linear(), should do one pass through the list and be linear O(n). The second function, called f_quadratic(), should compare each number to every other number on the list using nested loops giving a complexity of O(n^2). [By the way this is not a good algorithm, but we are doing it to illustrate the Big-O concept) To save you some time here is one way to write this function: deff_quadratic(x): min = x[0] I = len(x) for i in range(l): for jin range(i+1,1): if x[i]