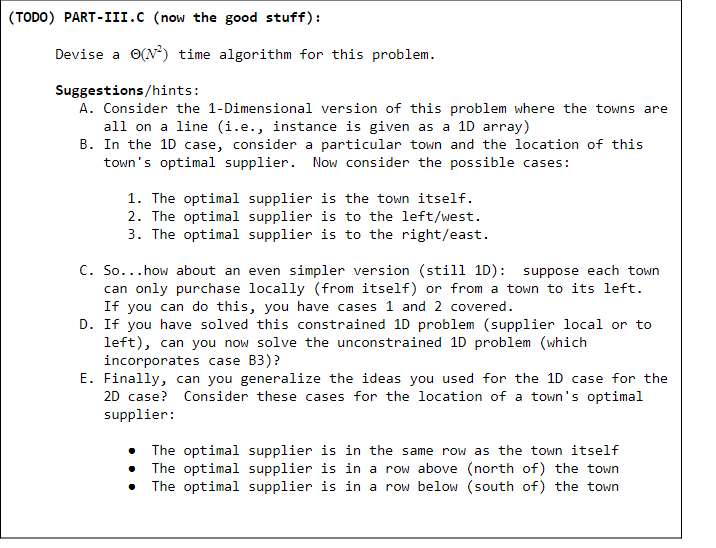
(Note: this is a "free-form" algorithm design problem -- don't assume, for example, that it must have something to do with divide-and conquer) N grid. You can imagine that each Everybody needs widgets! Our world is an N grid entry is a town. Every town has a widget vendor; the price of a widget in town ,1) is given as a positive number Wij. Every town also needs widgets and can purchase them from any town they like including from their local widget dealer. Transportation cost: to ship a widget from town ,j) to town (P.1) depends on the rectilinear distance between the towns and is given by: Tx (li pl+-91) where T is a given positive constant (transportation cost per unit distance). Thus, if town (1,3) decides to purchase widgets from town (P,9 the total cost per widget will be: wp.g+Tx (i-pl + lj-91) PROBLEM FORMULATION: We want to determine the cheapest way to buy widgets for every town and presumably the location of the vendor). For town (1.), let cu indicate the cheapest total cost: Cij = min (wp.g+T x (i-p[ + ] -91)) P.9{1.1) REMEMBER: Our task is compute/construct the entire cost-matrix -- i.e., the optimal total cost for every one of the N towns. (TODO) PART-III.A: Below is an example of a 3x3 widget price matrix. 1 2 1 4.0 2.5 2.0 5.0 5.0 4.0 3 6.0 4. 01 2.5 Assume for this example that the transportation cost per unit distance is T = 1.0. TASK: Construct the corresponding optimal cost matrix -- i.e., another 3 x 3 matrix giving for each town the following: 1. The cheapest total widget cost for the town. 2. The location (town coordinates) of the optimal widget vendor yielding the cheapest cost. We will call such a matrix an "optimal cost matrix. I'll get you started! Since town (1.3) has the cheapest widget price and transportation costs cannot be negative, the best choice for town (1,3) must be to "buy local. Thus, here is the optimal cost matrix with one of the entries already given: w 2.0 (1,3) (TODO) PART-III.B (more warm-up): Briefly describe a straightforward (N) time algorithm computing an optimal cost matrix from a given widget price matrix [] [] and transportation cost T. (TODO) PART-III.C (now the good stuff): Devise a (N2) time algorithm for this problem. Suggestions/hints: A. Consider the 1-Dimensional version of this problem where the towns are all on a line (i.e., instance is given as a 10 array) B. In the 1D case, consider a particular town and the location of this town's optimal supplier. Now consider the possible cases: 1. The optimal supplier is the town itself. 2. The optimal supplier is to the left/west. 3. The optimal supplier is to the right/east. C. So... how about an even simpler version (still 1D): suppose each town can only purchase locally (from itself) or from a town to its left. If you can do this, you have cases 1 and 2 covered. D. If you have solved this constrained 10 problem (supplier local or to left), can you now solve the unconstrained 10 problem (which incorporates case B3)? E. Finally, can you generalize the ideas you used for the 1D case for the 2D case? Consider these cases for the location of a town's optimal supplier: The optimal supplier is in the same row as the town itself The optimal supplier is in a row above (north of the town The optimal supplier is in a row below (south of the town (Note: this is a "free-form" algorithm design problem -- don't assume, for example, that it must have something to do with divide-and conquer) N grid. You can imagine that each Everybody needs widgets! Our world is an N grid entry is a town. Every town has a widget vendor; the price of a widget in town ,1) is given as a positive number Wij. Every town also needs widgets and can purchase them from any town they like including from their local widget dealer. Transportation cost: to ship a widget from town ,j) to town (P.1) depends on the rectilinear distance between the towns and is given by: Tx (li pl+-91) where T is a given positive constant (transportation cost per unit distance). Thus, if town (1,3) decides to purchase widgets from town (P,9 the total cost per widget will be: wp.g+Tx (i-pl + lj-91) PROBLEM FORMULATION: We want to determine the cheapest way to buy widgets for every town and presumably the location of the vendor). For town (1.), let cu indicate the cheapest total cost: Cij = min (wp.g+T x (i-p[ + ] -91)) P.9{1.1) REMEMBER: Our task is compute/construct the entire cost-matrix -- i.e., the optimal total cost for every one of the N towns. (TODO) PART-III.A: Below is an example of a 3x3 widget price matrix. 1 2 1 4.0 2.5 2.0 5.0 5.0 4.0 3 6.0 4. 01 2.5 Assume for this example that the transportation cost per unit distance is T = 1.0. TASK: Construct the corresponding optimal cost matrix -- i.e., another 3 x 3 matrix giving for each town the following: 1. The cheapest total widget cost for the town. 2. The location (town coordinates) of the optimal widget vendor yielding the cheapest cost. We will call such a matrix an "optimal cost matrix. I'll get you started! Since town (1.3) has the cheapest widget price and transportation costs cannot be negative, the best choice for town (1,3) must be to "buy local. Thus, here is the optimal cost matrix with one of the entries already given: w 2.0 (1,3) (TODO) PART-III.B (more warm-up): Briefly describe a straightforward (N) time algorithm computing an optimal cost matrix from a given widget price matrix [] [] and transportation cost T. (TODO) PART-III.C (now the good stuff): Devise a (N2) time algorithm for this problem. Suggestions/hints: A. Consider the 1-Dimensional version of this problem where the towns are all on a line (i.e., instance is given as a 10 array) B. In the 1D case, consider a particular town and the location of this town's optimal supplier. Now consider the possible cases: 1. The optimal supplier is the town itself. 2. The optimal supplier is to the left/west. 3. The optimal supplier is to the right/east. C. So... how about an even simpler version (still 1D): suppose each town can only purchase locally (from itself) or from a town to its left. If you can do this, you have cases 1 and 2 covered. D. If you have solved this constrained 10 problem (supplier local or to left), can you now solve the unconstrained 10 problem (which incorporates case B3)? E. Finally, can you generalize the ideas you used for the 1D case for the 2D case? Consider these cases for the location of a town's optimal supplier: The optimal supplier is in the same row as the town itself The optimal supplier is in a row above (north of the town The optimal supplier is in a row below (south of the town