NOTE - THIS IS A PRACTICE QUESTION ONLY - DO NOT REPORT - PLEASE REFER TO THE LINK BELOW
Please refer to this example before answering this Practice question -https://drive.google.com/file/d/1IWEsuGLkNmXh6w8FislwThJm1j4SfwxC/view?usp=sharing
Question: Complete the Correlation Coefficient and Regression question that examines the relationship between public school poverty rate and keystone math scores. - PLEASE DO NOT FORGET TO GRAPH ON PAGE 2 AND PAGE 4 (STEP 2) according to the example
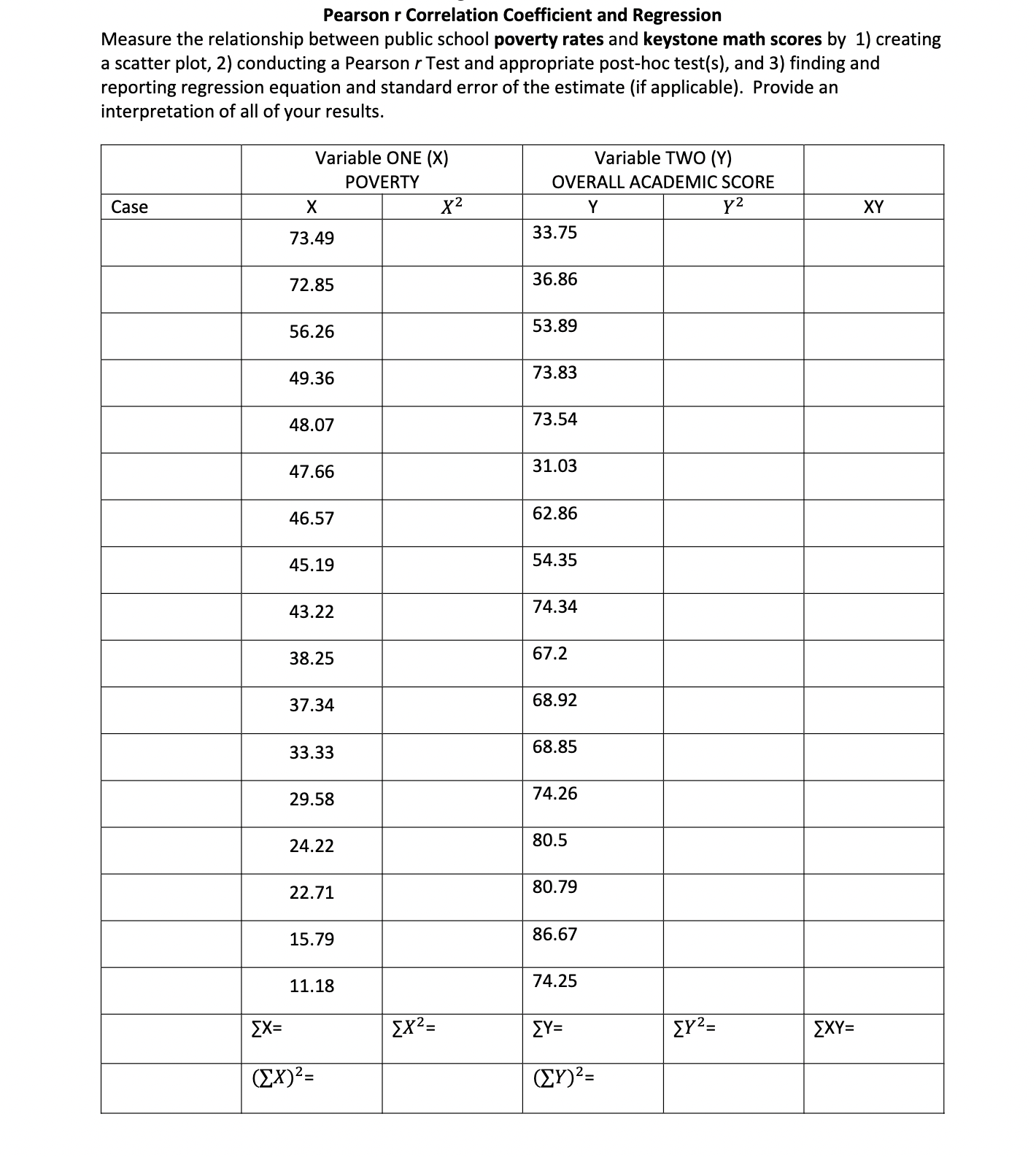
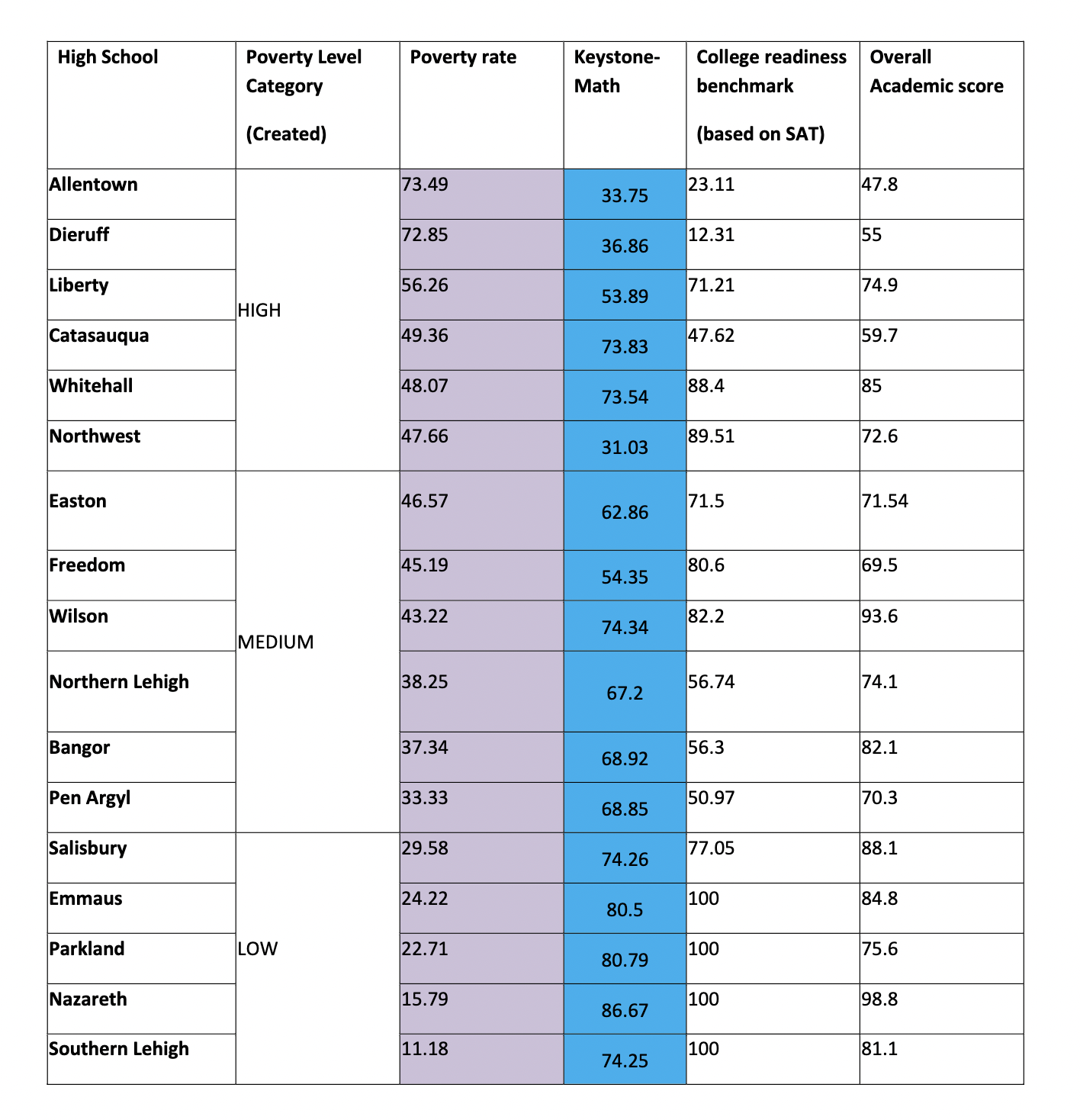
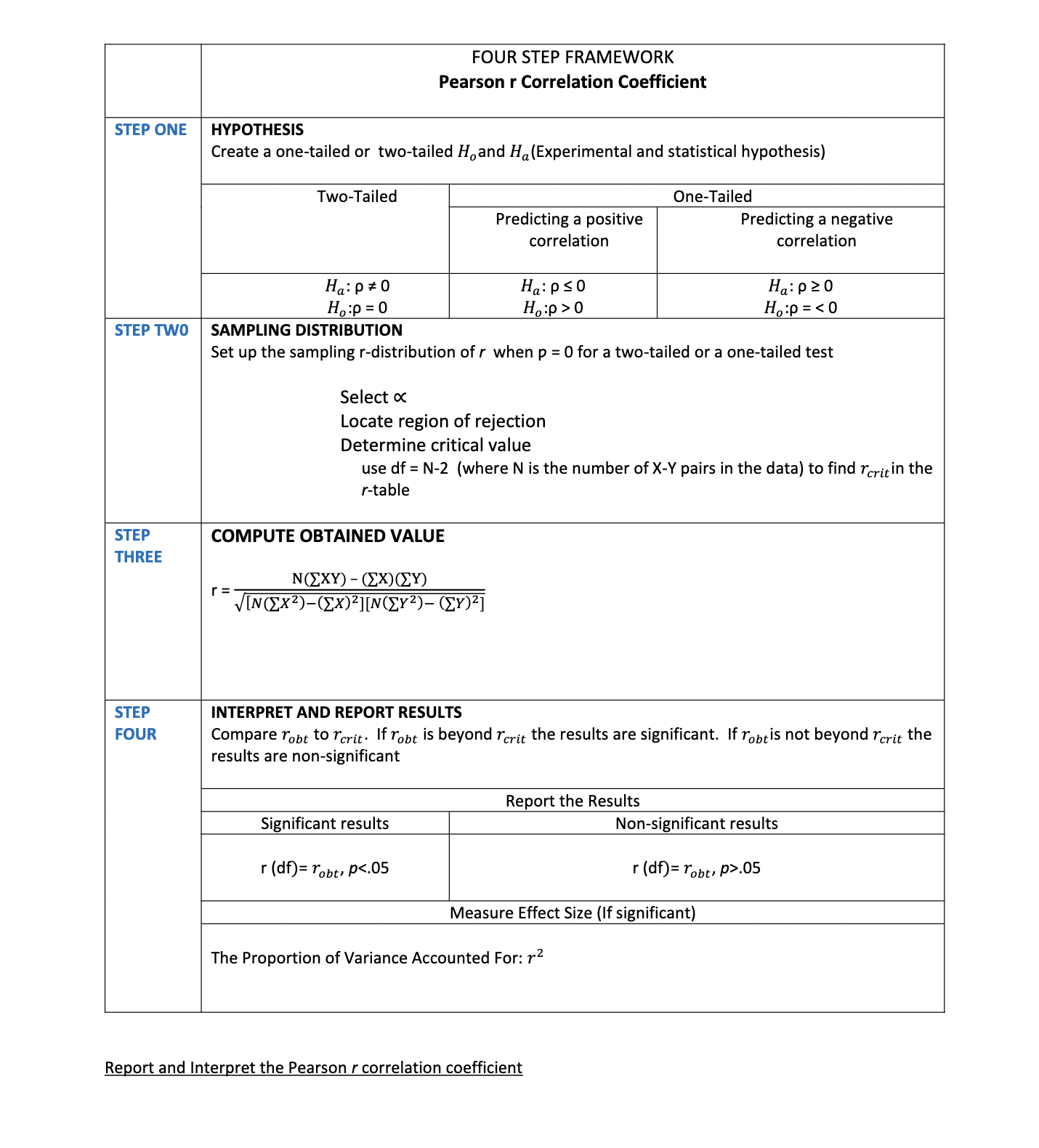
Pearson r Correlation Coefficient and Regression Measure the relationship between public school poverty rates and keystone math scores by 1) creating a scatter plot, 2) conducting a Pearson r Test and appropriate post-hoc test(s), and 3) finding and reporting regression equation and standard error of the estimate (if applicable). Provide an interpretation of all of your results. Variable ONE (X) Variable TWO (Y) POVERTY OVERALL ACADEMIC SCORE Case X X2 Y Y2 XY 73.49 33.75 72.85 36.86 56.26 53.89 49.36 73.83 48.07 73.54 47.66 31.03 46.57 62.86 45.19 54.35 43.22 74.34 38.25 67.2 37.34 68.92 33.33 68.85 29.58 74.26 24.22 80.5 22.71 80.79 15.79 86.67 11.18 74.25 [X= EX2= [Y= [Y2= [XY= (EX) 2= ([Y) 2=\fHigh School Poverty Level Poverty rate Keystone- College readiness Overall Category Math benchmark Academic score (Created) (based on SAT) Allentown 73.49 23.11 47.8 33.75 172.85 12.31 55 Dieruff 36.86 71.21 74.9 Liberty 56.26 53.89 HIGH 49.36 47.62 59. Catasauqua 73.83 Whitehall 48.07 188.4 85 73.54 Northwest 47.66 89.51 72.6 31.03 71.54 Easton 46.57 62.86 71.5 Freedom 145.19 80.6 69.5 54.35 93.6 Wilson 43.22 74.34 82.2 MEDIUM Northern Lehigh 38.25 74.1 67.2 56.74 37.34 156.3 82.1 Bangor 68.92 Pen Argyl 33.33 50.97 70.3 68.85 88.1 Salisbury 29.58 77.05 74.26 124.22 100 84.8 Emmaus 80.5 Parkland LOW 122.71 100 75.6 80.79 Nazareth 15.79 100 98.8 86.67 Southern Lehigh 11.18 100 81.1 74.25FOUR STEP FRAMEWORK Pearson r Correlation Coefficient STEP ONE HYPOTHESIS Create a one-tailed or two-tailed Ho and Ha (Experimental and statistical hypothesis) Two-Tailed One-Tailed Predicting a positive Predicting a negative correlation correlation Ha: P $ 0 Ha: PSO Ha: P 20 Ho:p = 0 Ho:p > 0 Ho:p = .05 Measure Effect Size (If significant) The Proportion of Variance Accounted For: r2 Report and Interpret the Pearson r correlation coefficientLinear Regression (Usually used when you are experimentally manipulating one variable) Compute "r\" and determine that it is significant. Proceed only if r is signicant. Determine your predictor (independent) variable (X) Determine your criterion (dependent) variable (Y) Compute the Linear Regression Equation: Y': bx + a (Enables us to find the value of a particular Y when we know b (the slope) and a (where Y intercepts)) Slope of the regression line (b) The Y intercept (or) b = NGXY) - (EXXEY) N(ZX2)-(ZX)2 Compute the Standard Error of the Estimate: (5Y1) (Determines the amount of error we expect to have when we use a relationship to predict Y scores) 5y! = (Syl (V1 - i\"2) Report and Interpret the Regression Eguation