Notes to help answer the question:

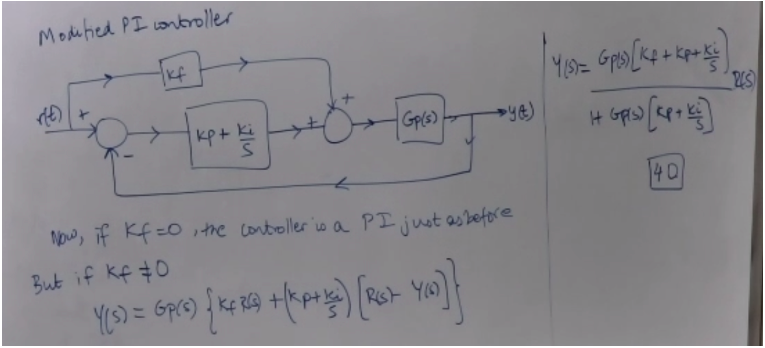
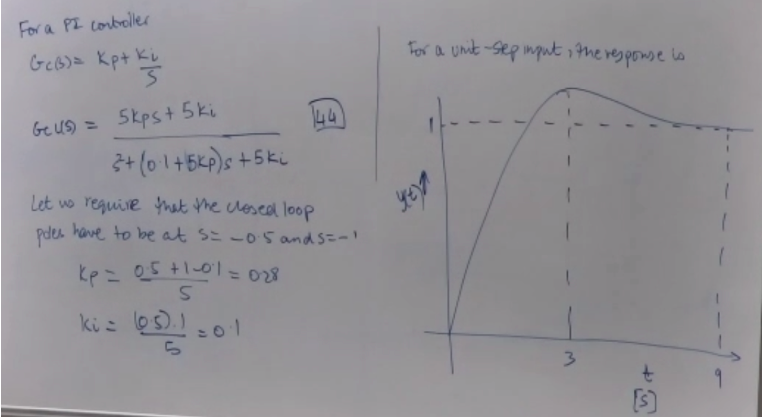
Consider a tank given by the differential equation = 0.5iv(t) - 0.50v(t), where y(t) is the level of liquid in the tank in inches, iv(t) is the position of the input valve, and ov(t) is the position of the output valve. Note that 0 siv(t) s 1 and 0 s ov(t) = 1. a) Design a modified Pl controller so that whenever ov(t) is equal to a constant, the steady-state error resulting from a constant reference input r(t) = L is equal to zero and the response is as fast as possible. Express your answer in terms of the controller gains Kp,Kp, K,. b) For the controller designed in (a), use Matlab to plot the response y(t) when y(0)=0, L= 10 in. and ov(t)=0.5 for t > 0 Please write clearly and label each part! The output response y) takes the form y(t) = rot ytred t70 35 set point Tracking a step response. In many problems, nt) is a step function That is given by to is a constant r(t) = ro for yo The objective of the controller is to ensure y(t)ro as to from some initial value y(0). Ytrit) >0 as t-> ro is the steadystate component of y(t) e(t)= r(t)- y(t) now, we know eft) = ro-[ro ty tr(t)) = -ytr@ for to The error signal is - times the transient signal of the output The PI controller "There are 3 major requirements for tracking a step reference. The real parts of the closed-loop poles must be less than zero. i.e. negative values. Let us suppose that +ki 137 2) To achieve steady-state eroor that is zero, it is necessary for Gp(s). Gc(s) to have a pole atsto 3) for the transants to be suitably fast, the closed-loop podes must be sufficiently for in the open left half place kp and ki are goin constants From the block diagram signal sent from Ge(s) to Gp(s) is CS) = G(S). E(S) C()= Kp Eco + k Els Inverse Laplace yields | (H) = Kp ett) + ki feleldo | 38 that is to allow the signeds to converge quickly Ge(s)= kpstki kpstki 139 KP Thus Gc (s) has a zero at sa-ki and a pole at szo This pole guarantees zero steady-state engor but does not provide any information or time frame when that will occur. We might want to consider modifying the controller to have the zero not entirely dependent on kp and ke Modified PI controller Y1912 Gpo[ky + Epose 25 VID) Gpls) -46) It Gis) (KP+ ki | ke + kg 40 Now, if Kf =0, the controller is a PI just as before But if kf&0 YC05 670) {rease the ) [ect yo) } Breaking this down into numerator and denominator conboller is nolonger completely and solely dependent I gains 29 polynomials YER = NAIS) [(kytke)s + ki] on the control DPIS) 5 + Np(s) Ckps+ki) This results in Gulls Npsy [lef+kp) stri) 141 Dpis) st Npro) kostki If kf=0, 14) will be the same as the PI controler, Here though, a zero location will be at (KftKP)s tkito .s= -ki Ketke Km is the motor constant, Olt) is the motor PI control of a DC moter. DE for a DC motor is aot) at tike dhe ed ect) = Km 'VCE 142 =, The objective is to control the velocity of the motor shaft &cts specifically & t) - Bult as tree id is the desired velocity I-1 Laplace Transform of 142 is kd=01 km = 5 sols + ko 3 = km VS I Kd is the viscous friction coefficient of the motor and the load I is the moment of inertia of the motor km and the load 143 stkol TF is Gp(8= YCS 11 stko shaft angle and it is the voltage input to the I field arenit of the motor. For a PI controller For a unit-step input, the response is G pt kus GcB)= xptki 44 Geus) = 5kpst 5ki 3+ (0.1+5KP)s +5ki Let us require that the closed loop pdes have to be at s= -0.5 and 5=-1 Kp = 0.5 +1 -01 = 028 5 ki= 10.5). 3 t further out in the OLHP than 5=-1;5=-0.5 The response of the conboller to the poles being at 5=-1 and 32-05 is relatively slow. To achieve a faster response, we can pick pole locations | Gus= 5(44tke)s + ski +6145kp)s +ski 145 However the overshoot seen in the response will increase We are going to choose ky so that the zero cancels out one of the poles The modified PI controller can be of assistance. = ( RS The modified PI controller. Inserting Gp(s) = 5 That results in Kp =078, ki = 08 and thus Kf = -0.38 into the equation above Stol ya dia Consider a tank given by the differential equation = 0.5iv(t) - 0.50v(t), where y(t) is the level of liquid in the tank in inches, iv(t) is the position of the input valve, and ov(t) is the position of the output valve. Note that 0 siv(t) s 1 and 0 s ov(t) = 1. a) Design a modified Pl controller so that whenever ov(t) is equal to a constant, the steady-state error resulting from a constant reference input r(t) = L is equal to zero and the response is as fast as possible. Express your answer in terms of the controller gains Kp,Kp, K,. b) For the controller designed in (a), use Matlab to plot the response y(t) when y(0)=0, L= 10 in. and ov(t)=0.5 for t > 0 Please write clearly and label each part! The output response y) takes the form y(t) = rot ytred t70 35 set point Tracking a step response. In many problems, nt) is a step function That is given by to is a constant r(t) = ro for yo The objective of the controller is to ensure y(t)ro as to from some initial value y(0). Ytrit) >0 as t-> ro is the steadystate component of y(t) e(t)= r(t)- y(t) now, we know eft) = ro-[ro ty tr(t)) = -ytr@ for to The error signal is - times the transient signal of the output The PI controller "There are 3 major requirements for tracking a step reference. The real parts of the closed-loop poles must be less than zero. i.e. negative values. Let us suppose that +ki 137 2) To achieve steady-state eroor that is zero, it is necessary for Gp(s). Gc(s) to have a pole atsto 3) for the transants to be suitably fast, the closed-loop podes must be sufficiently for in the open left half place kp and ki are goin constants From the block diagram signal sent from Ge(s) to Gp(s) is CS) = G(S). E(S) C()= Kp Eco + k Els Inverse Laplace yields | (H) = Kp ett) + ki feleldo | 38 that is to allow the signeds to converge quickly Ge(s)= kpstki kpstki 139 KP Thus Gc (s) has a zero at sa-ki and a pole at szo This pole guarantees zero steady-state engor but does not provide any information or time frame when that will occur. We might want to consider modifying the controller to have the zero not entirely dependent on kp and ke Modified PI controller Y1912 Gpo[ky + Epose 25 VID) Gpls) -46) It Gis) (KP+ ki | ke + kg 40 Now, if Kf =0, the controller is a PI just as before But if kf&0 YC05 670) {rease the ) [ect yo) } Breaking this down into numerator and denominator conboller is nolonger completely and solely dependent I gains 29 polynomials YER = NAIS) [(kytke)s + ki] on the control DPIS) 5 + Np(s) Ckps+ki) This results in Gulls Npsy [lef+kp) stri) 141 Dpis) st Npro) kostki If kf=0, 14) will be the same as the PI controler, Here though, a zero location will be at (KftKP)s tkito .s= -ki Ketke Km is the motor constant, Olt) is the motor PI control of a DC moter. DE for a DC motor is aot) at tike dhe ed ect) = Km 'VCE 142 =, The objective is to control the velocity of the motor shaft &cts specifically & t) - Bult as tree id is the desired velocity I-1 Laplace Transform of 142 is kd=01 km = 5 sols + ko 3 = km VS I Kd is the viscous friction coefficient of the motor and the load I is the moment of inertia of the motor km and the load 143 stkol TF is Gp(8= YCS 11 stko shaft angle and it is the voltage input to the I field arenit of the motor. For a PI controller For a unit-step input, the response is G pt kus GcB)= xptki 44 Geus) = 5kpst 5ki 3+ (0.1+5KP)s +5ki Let us require that the closed loop pdes have to be at s= -0.5 and 5=-1 Kp = 0.5 +1 -01 = 028 5 ki= 10.5). 3 t further out in the OLHP than 5=-1;5=-0.5 The response of the conboller to the poles being at 5=-1 and 32-05 is relatively slow. To achieve a faster response, we can pick pole locations | Gus= 5(44tke)s + ski +6145kp)s +ski 145 However the overshoot seen in the response will increase We are going to choose ky so that the zero cancels out one of the poles The modified PI controller can be of assistance. = ( RS The modified PI controller. Inserting Gp(s) = 5 That results in Kp =078, ki = 08 and thus Kf = -0.38 into the equation above Stol ya dia