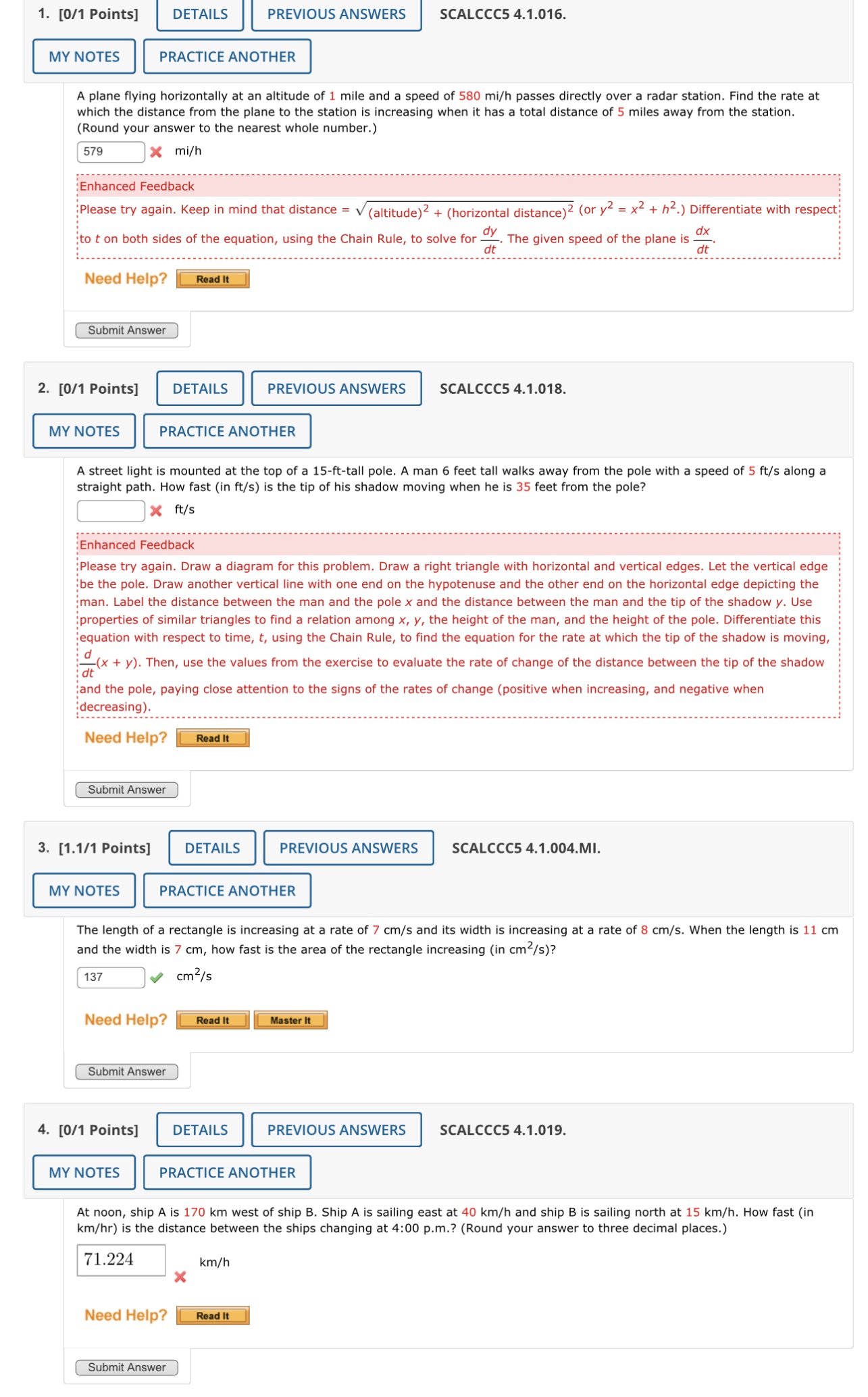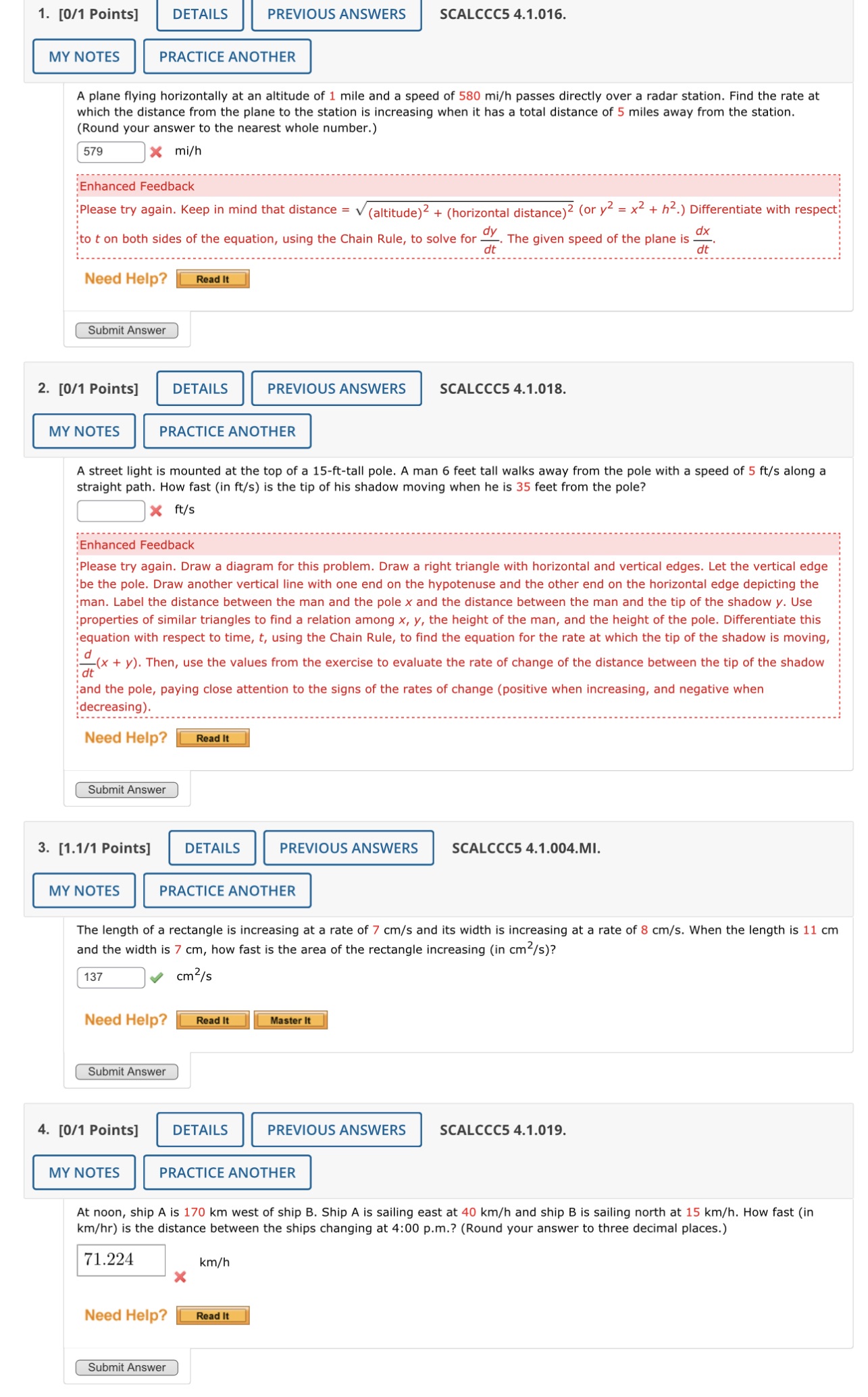
Number 1 , 2 , and 4 in the photo below. Calculus 1 , please solve the problem and show your work.
1. [0/1 Points] DETAILS PREVIOUS ANSWERS SCALCCC5 4.1.016. MY NOTES PRACTICE ANOTHER A plane flying horizontally at an altitude of 1 mile and a speed of 580 mi/h passes directly over a radar station. Find the rate at which the distance from the plane to the station is increasing when it has a total distance of 5 miles away from the station. (Round your answer to the nearest whole number.) 579 X mi/h :Enhanced Feedback Please try again. Keep in mind that distance = v (altitude) 2 + (horizontal distance)2 (or y = x2 + h2.) Differentiate with respect :to t on both sides of the equation, using the Chain Rule, to solve for . The given speed of the plane is _ dt dt Need Help? Read It Submit Answer 2. [0/1 Points] DETAILS PREVIOUS ANSWERS SCALCCC5 4.1.018. MY NOTES PRACTICE ANOTHER A street light is mounted at the top of a 15-ft-tall pole. A man 6 feet tall walks away from the pole with a speed of 5 ft/s along a straight path. How fast (in ft/s) is the tip of his shadow moving when he is 35 feet from the pole? * ft /s Enhanced Feedback Please try again. Draw a diagram for this problem. Draw a right triangle with horizontal and vertical edges. Let the vertical edge be the pole. Draw another vertical line with one end on the hypotenuse and the other end on the horizontal edge depicting the man. Label the distance between the man and the pole x and the distance between the man and the tip of the shadow y. Use properties of similar triangles to find a relation among x, y, the height of the man, and the height of the pole. Differentiate this equation with respect to time, t, using the Chain Rule, to find the equation for the rate at which the tip of the shadow is moving, dt - (x + y). Then, use the values from the exercise to evaluate the rate of change of the distance between the tip of the shadow and the pole, paying close attention to the signs of the rates of change (positive when increasing, and negative when decreasing). Need Help? Read It Submit Answer 3. [1.1/1 Points] DETAILS PREVIOUS ANSWERS SCALCCC5 4.1.004.MI. MY NOTES PRACTICE ANOTHER The length of a rectangle is increasing at a rate of 7 cm/s and its width is increasing at a rate of 8 cm/s. When the length is 11 cm and the width is 7 cm, how fast is the area of the rectangle increasing (in cm/s)? 137 cm 2/s Need Help? Read It Master It Submit Answer 4. [0/1 Points] DETAILS PREVIOUS ANSWERS SCALCCC5 4.1.019. MY NOTES PRACTICE ANOTHER At noon, ship A is 170 km west of ship B. Ship A is sailing east at 40 km/h and ship B is sailing north at 15 km/h. How fast (in km/hr) is the distance between the ships changing at 4:00 p.m.? (Round your answer to three decimal places.) 71.224 km/h X Need Help? Read It Submit