NUMERICAL METHODS

The following is a plot of the function f(x) = sin(x³) + x² :

My code and output is:

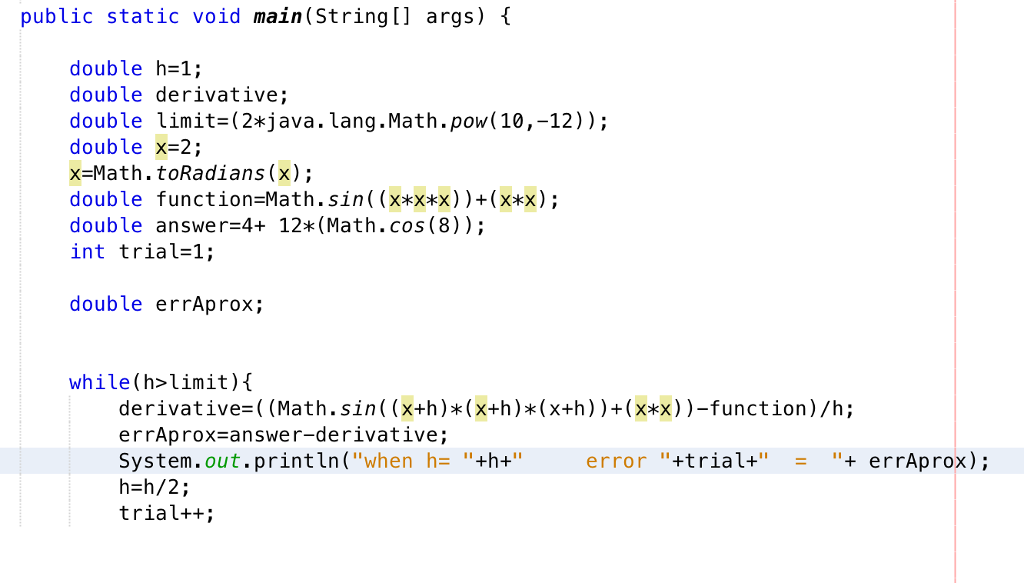
OUTPUT:

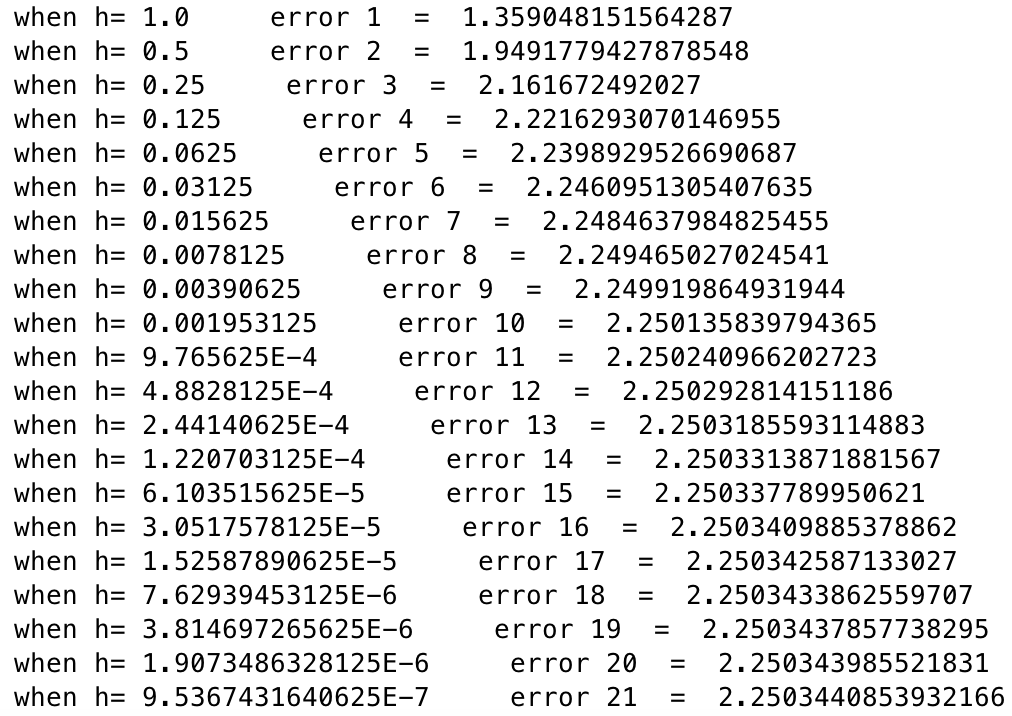
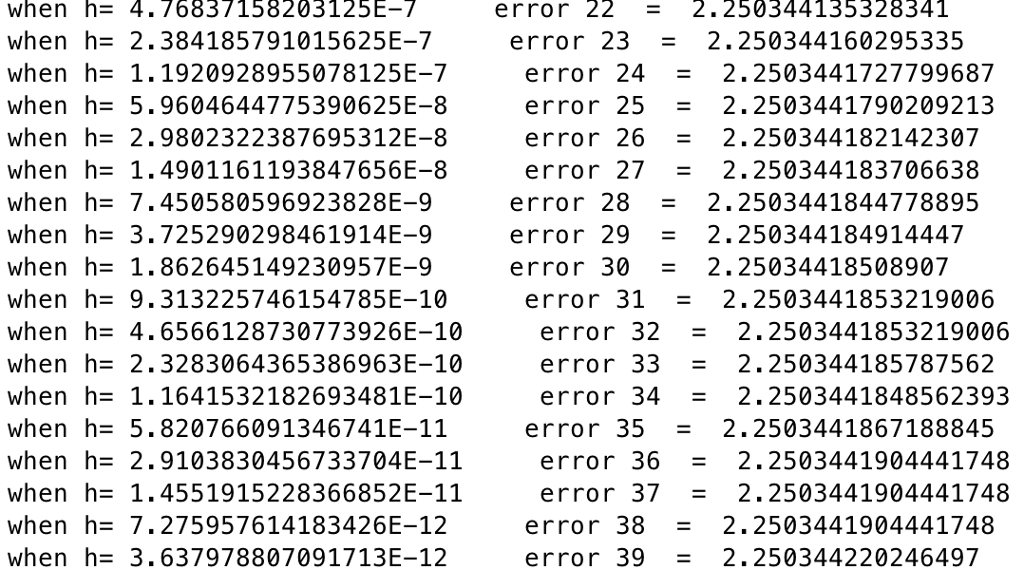
Question: Am I doing it right? Can you help me write the conclusion

In order to illustrate the effects of the two major error sources, rounding and truncation, attempt to determine an approximation to the derivative of f(x) at x = 2.0 radians using the difference approximation given below. (The true answer is 4 + 12 cos(8) or about 2.2539995942966376896) Use the formula f' (x) (f (xth) - f (x)) / h with h-1,0.5,0.25, 1.8189894035459e-12 i.c., keep halving h until it is less than 2.0c-12.) Print out the values of h, your approximation tof(x), and the error in the approximation for each value of h used. This error will include the effects of both truncation and rounding Write down (in your output file or in another file submitted with your program) any conclusions that you can make from these experiments