Objective : Railroad Permutation Stack Problem with 1 Stack

The purpose of this assignment is to gain experience with the applications of stack ADT.

Project Description Consider the following railway switching system:

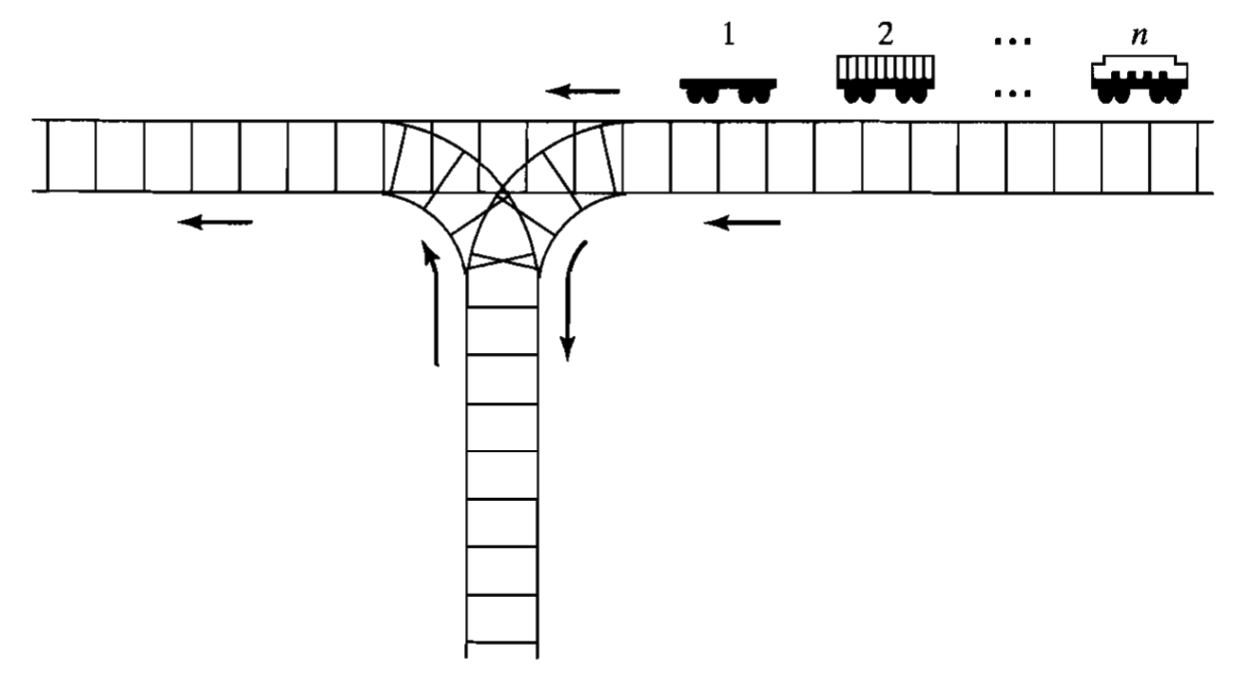
Railroad cars numbered 1,2, ..., n on the right track are to be permuted and moved along on the left track. A car may be moved directly onto the left track, or it may be shunted onto the siding to be removed at a later time and placed on the let track. The siding thus operates as a stack, a push operation moving a car from the right track onto the siding and a pop opera!on moving the "top" car from the siding onto the le" track. For example, when n = 3, push 1, push 2, move 3, pop 2, pop 1 arranges them in the order 3, 2,1.

Are any permutations not possible? Yes, for example, 312 is an impossible permutation.

Assume that the train arriving from the direction A has N

You can assume that single coaches can be disconnected from the train before they enter the sta!on and that they can move un!l they are on the track in the same direction. You can also suppose that at any !me there can be located as many coaches as necessary in the sta!on. But once a coach has entered the sta!on it cannot return to the track on the right and also once it has le" the sta!on in the direc!on on the le" it cannot return back to the sta!on.

Input

The input file consists of blocks of lines, each of which is a test case. Each block except the last describes one train and possibly more requirements for its reorganization. In the first line of the block, there is the integer N, which is the number of coaches in the train. In each of the next lines of the block there is a permutation of 1, 2, ..., N . For example, if N is 5, the permutation could be 5, 3, 2, 1, 4. Your program will take this permutations as input and determine whether you can marshal the coaches from the right track an incoming order 1, 2, 3, 4, 5 to the le" track with an outgoing order 5, 3, 2, 1, 4 using the sta!on, which can be treated as a stack.

The last line of the block contains just 0. If a block starts with a zero, the program will terminate.

Output

The output file contains the lines corresponding to the lines with permutations in the input file. A line of the output file contains Yes if it is possible to marshal the coaches in the order required on the corresponding line of the input file. Otherwise, it contains No. In addi!on, there is one empty line after the lines corresponding to one block of the input file. There is no line in the output file corresponding to the last null block of the input file.

Sample Input:

5 start of the first block

12345

54123

43521

0 end of the first block 6 start of the second block

654321

342516

0 end of the second block 0

end of input

Sample Output:

Yes

No

Yes

Yes

Yes

Note:

2. You should apply stack ADT in the program. You can use the Standard Template Library (STL) stack instead of Stack class defined in the lectures.

Here is an example of how to use the STL stack push/pop/top and empty func!ons which will be used in this project.

#include  #include  using namespace std; 

int main ()

{ stack mystack; // Notice the element type in the stack should be specified in the ang 

le bracket. for (int i=0; i 
 cout  
 { cout  
 mystack.pop(); } 
 
cout  
return 0; }
 
 
 
Challenge (Bonus 5 points)
 
In general, what permutation of the sequence 1, 2, ... , n can be obtained when a stack is used in this manner?
 
 
 
note* it would be great if the code would be in C++, using stacks and vectors only. An iterative method would be more appreciated rather than a recursive method.
 
Thank You.