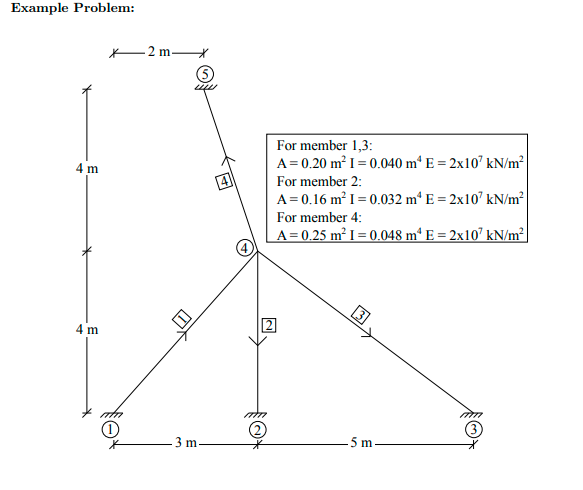
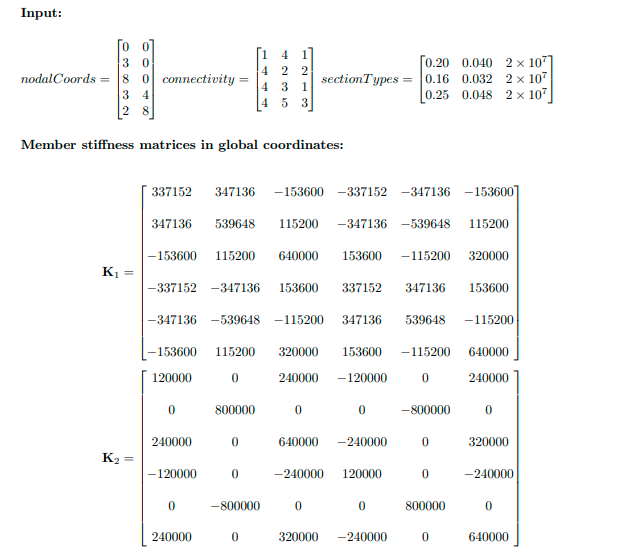
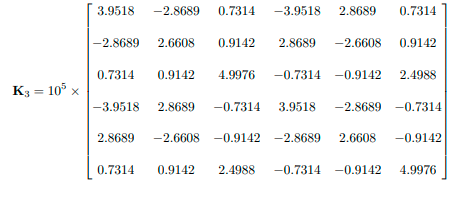
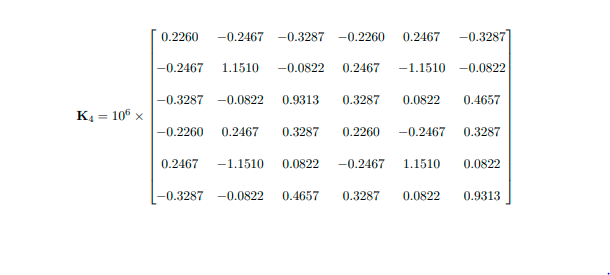
Objective: To develop functions calculating stiffness matrices in local and global coordinates, and trans- formation matrix for a given frame member. An example is given below. You are free whether to follow the given approach or develop your own approach as long as you achieve the objective. Develop three MATLAB functions. The first function member_stiffness_matrix shall calculate the stiffness matrix of a given member in local coordinates. The function may be in the form: k_local = member_stiffness matrir-local(nodeInfo.sectionInfo) where nodeInfo is a matrix having a size (2 x 2), the first row of which consists of the X coordinate (first column) and the Y coordinate (second column) of the beginning node and the second row of which consists of the X coordinate (first column) and the Y coordinate (second column) of the end node, sectionInfo is a vector having a size (1 x 3) consisting of the cross-sectional area (first column), the moment of inertia (second column) and the modulus of elasticity (third column). The second function transformation matrix shall calculate the transformation matrix for a given mem- ber. The function may be in the form: T = transformation matriz (nodeInfo) where nodeInfo is a vector having a size (2 x 2), the first row of which consists of the X coordinate (first column) and the Y coordinate (second column) of the beginning node and the second row of which consists of the X coordinate (first column) and the Y coordinate (second column) of the end node. The third function member-stiffness-matrir-global shall transform a given member stiffness matrix from local coordinates to global coordinates. The function may be in the form: k_global = member stiffness_matriz_global (memberID, nodalCoords,connectivity.section Types) a where memberID is the ID number of the member for which the stiffness matrix will be calculated, nodalCoords is a matrix having a size (Number of Nodes x 2), each row of which consist of the X coordinate (first column) and the Y coordinate second column) of the node with ID number equal to the row number, connectivity is a matrix having a size (Number of Members x 3), each row of which consist of the ID number of beginning node (first column), the ID number of end node (second column) and the ID number of section type (third column) of the member with ID number equal to the row number, section Types is a matrix having a size (Number of Section Types x 3), each row of which consist of the cross-sectional area (first column), the moment of inertia (second column) and the modulus of elasticity of the section type with ID number equal to the row mimber. The function member stiffness_matriz_global will first call the functions member stiffness matric_local to calculate the stiffness matrix of the given given member in local coordinates and transform_local2global to calculate the transformation matrix for the given member, and then transform the member stiff- ness matrix returned by the function member stiffness_matric_local from local coordinates to global coordinates. Example Problem: X -2 m 3 4 m For member 1,3: A=0.20 mI=0.040 m E = 2x10 kN/m For member 2: A=0,16 mI=0.032 mE = 2x10 kN/m For member 4: A = 0.25 m I = 0.048 m E = 2x10 kN/m 4 m 3 m -5 m Input: 3 0 nodalCoords = 8 o connectivity 3 4 28 [i 4 1 4 2 2 4 3 1 4 5 [0.20 0.040 2 x 107] section Types = 0.16 0.032 2 x 107 (0.25 0.048 2 x 107 Member stiffness matrices in global coordinates: 337152 347136 -153600 -337152 -347136 -153600] 347136 539648 115200 -347136 -539648 115200 -153600 115200 640000 153600 -115200 320000 K1 = -337152 -347136 153600 337152 347136 153600 -347136 -539648 -115200 347136 539648 -115200 115200 320000 153600 -115200 -153600 120000 640000 240000 0 240000 - 120000 0 0 800000 0 0 -800000 0 240000 0 640000 - 240000 0 320000 K2= - 120000 0 - 240000 120000 0 - 240000 0 -800000 0 0 800000 0 240000 0 320000 - 240000 0 640000 3.9518 -2.8689 0.7314 -3.9518 2.8689 0.7314 -2.8689 2.6608 0.9142 2.8689 -2.6608 0.9142 0.7314 0.9142 4.9976 -0.7314 -0.9142 2.4988 K3 = 10% -3.9518 2.8689 -0.7314 3.9518 -2.8689 -0.7314 2.8689 -2.6608 -0.9142 -2.8689 2.6608 -0.9142 0.7314 0.9142 2.4988 -0.7314 -0.91424.9976 0.2260 -0.2467 -0.3287 -0.2260 0.2467 -0.3287 -0.2467 1.1510 -0.0822 0.2467 -1.1510 -0.0822 -0.3287 -0.0822 0.9313 0.3287 0.0822 0.4657 K4 = 106 x -0.2260 0.2467 0.3287 0.2260 -0.2467 0.3287 0.2467 -1.1510 0.0822 -0.2467 1.1510 0.0822 -0.3287 -0.0822 0.4657 0.3287 0.0822 0.9313