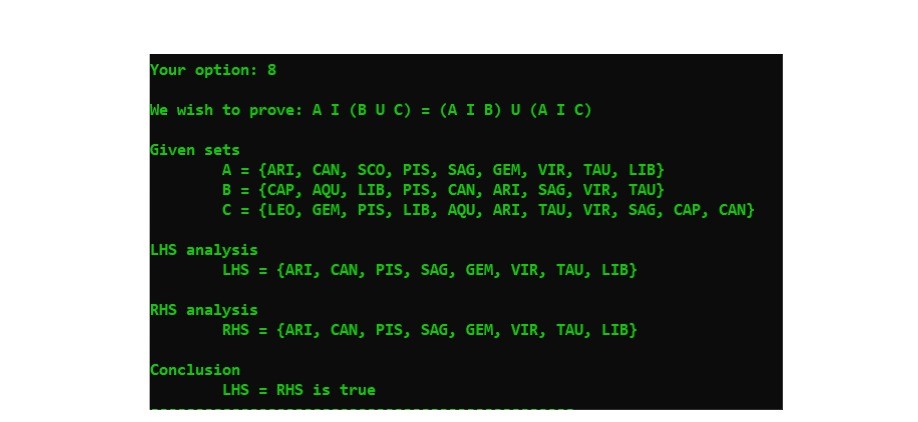
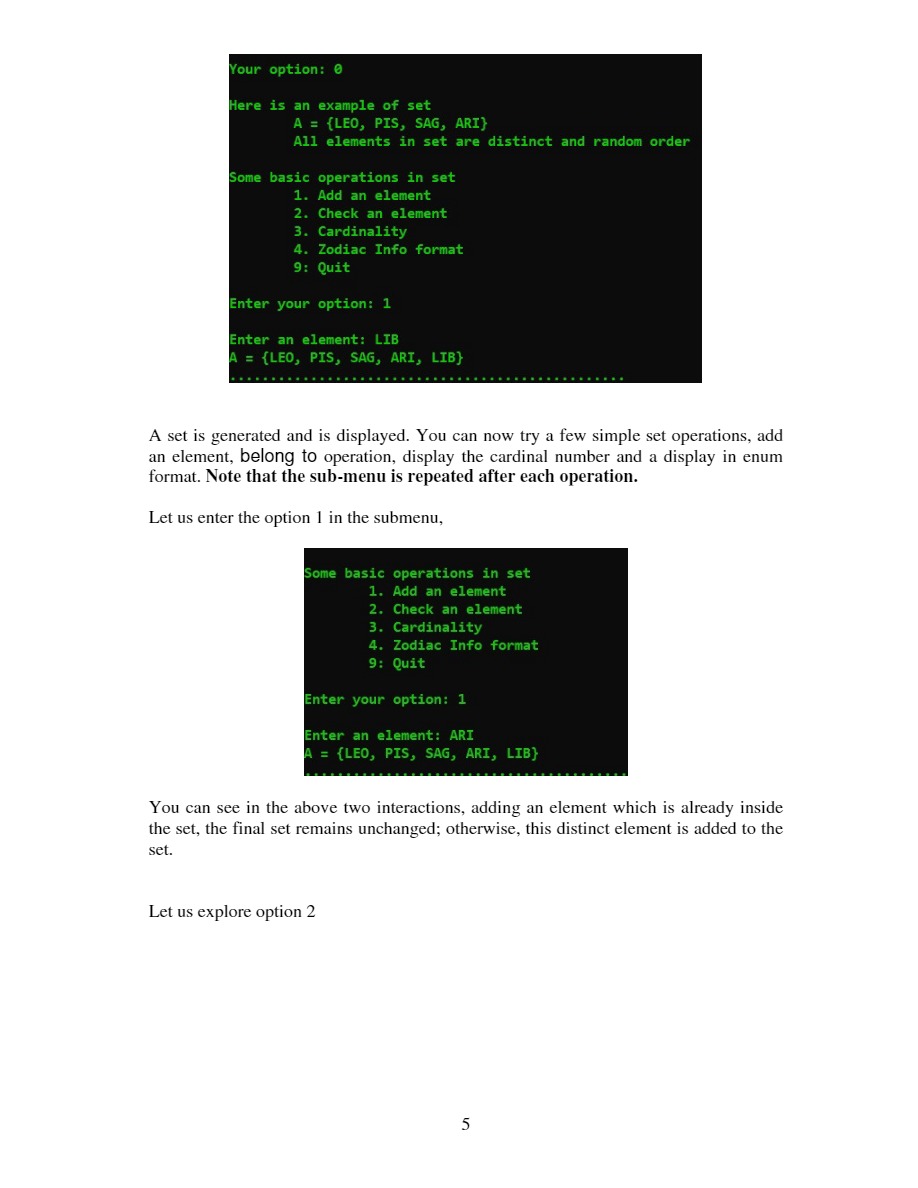
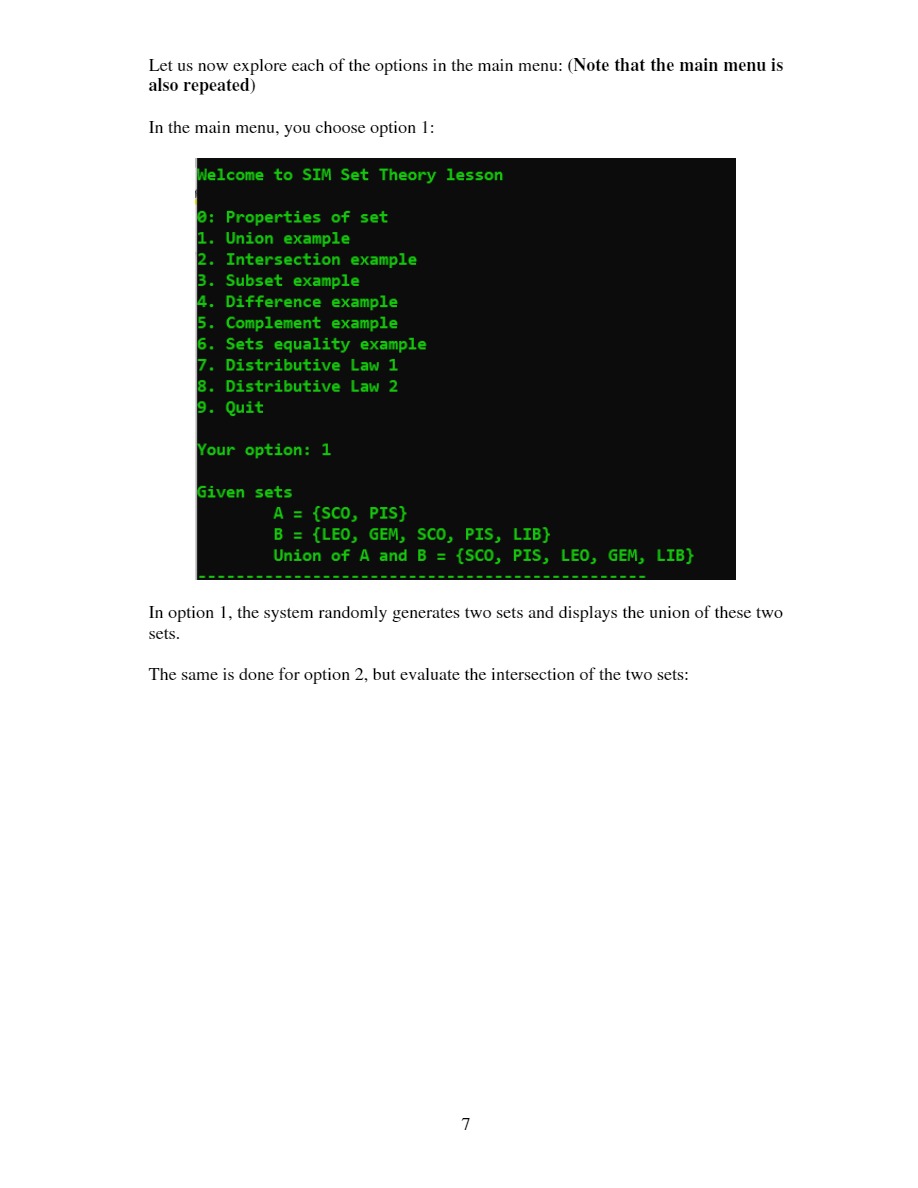
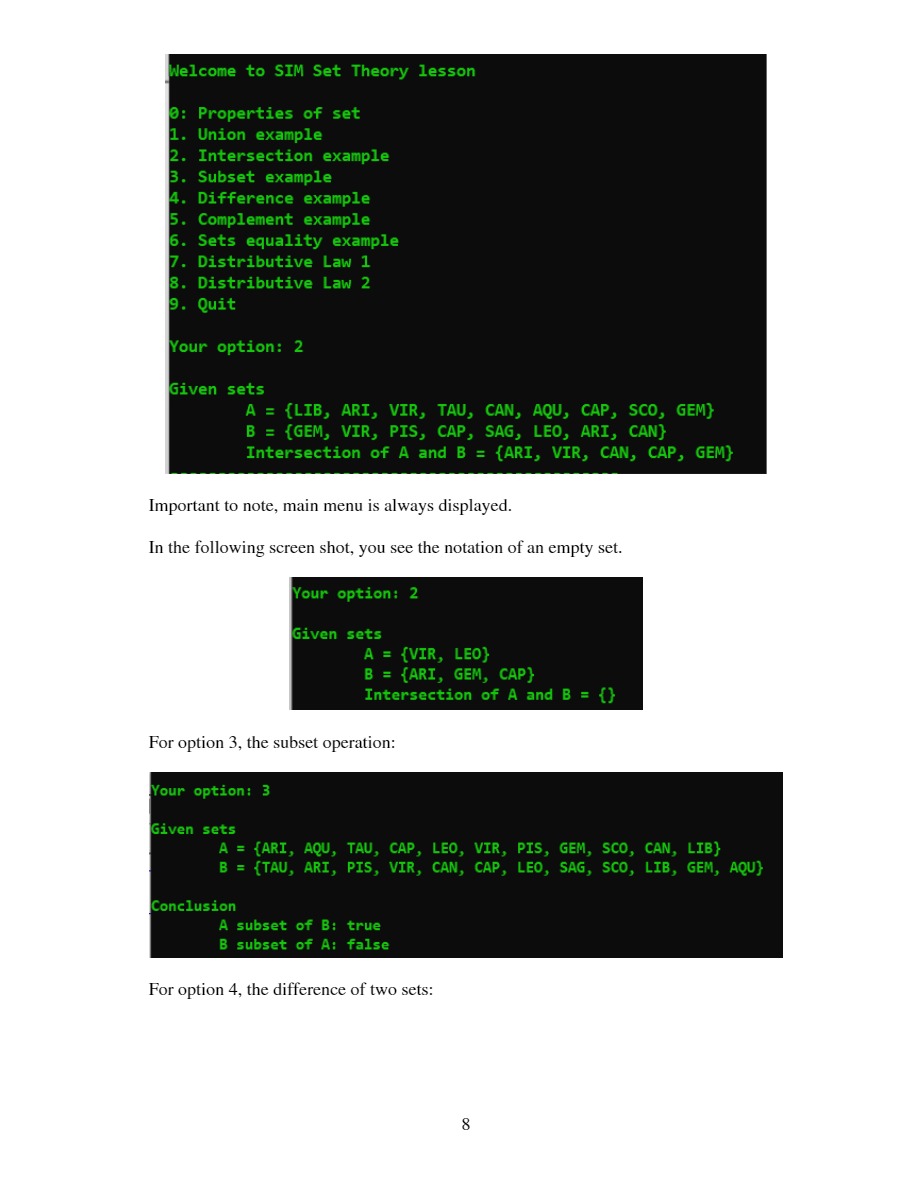
Objectives: Practice java programming with classes and objects, constructors, copy constructors, enum type, array, ArrayList (generic version), overloaded methods, passing by reference etc. Task (6 marks) In mathematics, a set is a collection of distinct elements and elements in a set are not in order. Here are some examples of sets: Option 7 and 8 are two distributive laws: Distributive Law states that, the sum and product remain the same value even when the order of the elements is altered. First Law: AU (BNC) = (AUB) n (AUC) Second Law: An (BUC) (ANB) U (ANC) We use symbol "I" for intersection in display: Let us explain the 1st law We first compute the expression on the left-hand side. To do this, you need to compute (BNC) and then A U (BNC). To compute the expression on the right-hand side, you need to compute (A U B), (AUC) and then (AUB) N (AUC). Your option: 7 We wish to prove: A U (B I C) = (A U B) I (A U C Given sets A = {CAN, ARI, SAG, AQU, GEM, TAU} B = {SAG, LIB, PIS, ARI, AQU, SCO, VIR, CAP, TAU, CAN} C = {SCO, LIB, LEO, SAG, AQU, VIR} LHS analysis LHS = {CAN, ARI, SAG, AQU, GEM, TAU, LIB, SCO, VIR} RHS analysis RHS = {CAN, ARI, SAG, AQU, GEM, TAU, LIB, SCO, VIR} Conclusion LHS = RHS is true Same analysis can be done for 2nd law: 10 Your option: 8 We wish to prove: A I (B U C) = (A I B) U (A I C) Given sets A = {ARI, CAN, SCO, PIS, SAG, GEM, VIR, TAU, LIB} B = {CAP, AQU, LIB, PIS, CAN, ARI, SAG, VIR, TAU} C = {LEO, GEM, PIS, LIB, AQU, ARI, TAU, VIR, SAG, CAP, CAN} LHS analysis LHS = {ARI, CAN, PIS, SAG, GEM, VIR, TAU, LIB} RHS analysis RHS = {ARI, CAN, PIS, SAG, GEM, VIR, TAU, LIB} Conclusion LHS = RHS is true (a) A set of integers, e.g. integerSet = {3, 1, 4, 2} (b) A set of fruits, e.g. fruitSet = {apple, orange, papaya} (c) A set of characters, e.g. charSet = {'A', 'm', '&'} We always enclose elements of sets inside a pair of { }. Here are some other properties on sets: (1) A set can be empty, i.e. no element. We call it empty set. In mathematics, we have a special symbol to denote empty set. Convenient to our design later, we will use { } to denote an empty set. (2) When checking an element is inside a set. We call it "belong to". (3) If a set contains in another set, we call it subset. For example, {1, 2, 3} is a subset of {2, 3, 4, 6, 1}. Therefore, empty set is a subset of every set. (4) The cardinal number of a set is the number of elements in a set. (5) The union of two sets A and B are all the elements belong to A and B, minus the duplications. For example, if A = {1, 2, 3} and B = {2, 3, 4, 5}, the union is {1, 2, 3,4,5). (6) The intersection of two sets A and B are the common elements of A and B. Using the example quoted in (5), the intersection is {2, 3}. (7) The equality of two sets A and B are all the elements of A are in B and all the elements of B are in A. Or alternatively, A is the subset of B and vice versa. (8) The difference of two sets A and B, for example A - B, is those elements in B should not be in A. For example, if A-{1, 2, 3) and B (2, 3, 4, 5), A-B={1} and B - A = {4, 5}. We have all the required properties for our task. In this assignment, our universal set is the 12 enumeration constants of zodiac signs together with their range of dates. They are II Aries Mar 21 - Apr 19 Taurus Apr 20 - May 20 Gemini May 21 - Jun 20 Cancer Jun 21 - Jul 22 Libra Sep 23 - Oct 22 m Scorpio Oct 23 - Nov 21 Sagittarius Nov 22 - Dec 21 50 Capricorn Dec 22 - Jan 19 Leo Jul 23-Aug 22 M M Aquarius Jan 20 - Feb 18 m Virgo Aug 23 - Sep 22 H Pisces Feb 19 - Mar 20 2 Data validation is not necessary in this design, when "I" want to add in a sign, you can assume that this is a valid sign in the enumeration constants; i.e. we have restricted ourselves in a subset of the above 12 signs. The best way to test your design is to develop an educational system to teach some basic set theory. All the sets used in your design should be randomly generated by the system i.e. the sizes (also known as cardinal number, from 0 to 12 elements) and the elements. Let us explore the following UML diagram for the whole task: < > ZodiacInfo Aries Taurus Gemini GEM A Cancel A CAN Leo LEO Virgo AVIR A Libra Scorpio Sagittarius Capricom Aquarius Pisces > Zodiac Type AARI TAU 800 ASAC ACAP AQU APIS Set -ArrayList s ++Set(Set otherSet) +boolean isEmpty() +int cardinality +boolean belongTo(ZodiacType element) void addElement(Zodiac Type element) +boolean subset(Set otherSet) +void union(Set otherSet) void intersection(8at otherSat) +vold difference(Set other Set +Set complement boolean equality(8et otherSet) + String toStringo +String getZodiacInfoFormat() YourName A1 -static Scanner input -static void displayZodiacTypeInfo -static ZodiacType getAnElement -static Set nataSat static void displayMenu -static void unionExample) -static void intersectionExample) -static void subsetExample -static void differenceExample)) -static void complementExample) static void equalityExample -static void distributiveLaw 10 -static void distributive Law 20 + static void displaySubmenu +static void anExample)) +static void main(Stinall aris) Let us look at each of the classes Enumeration class Zodiac Info This is a simple enum class consisting of the 12 zodiac constants (b) Enumeration class ZodiacType This is the universal set that a subset is constructed. Each enum constant has three descriptions: a constant from enum Zodiac Info, starting date, ending date. Refer to page 4 for information required for this universal set. (b) Class Set We use an array list to represent a set, which is an instance variable defined inside the class. The normal set operations: belong to, contains, union, intersection, complement, difference, subset, equality is some of the set's operations. The toString method returns a String of enum type enclosed between braces, for example {LIB, ARI} and the getZodiacInfoFormat method returns its equivalent in enum info, for example {Libra, Aries} according to the above example. 3 You should use the default constructor to construct an empty set. Do some deep copying in the copy constructor; you may need this constructor to perform some of the subtasks. (c) Main class We now ready to present the whole system. You are required to design an educational system to teach basic set theory. We propose the following interactions for your system: When you execute your program, the system will display the info for the universal set (a call to display Zodiac Info method, display once only) and followed by a menu (the display of menu is repeated after an operation) Universal set info Zodiac Type Zodiac Info ARI Aries From Date March 21 TAU Taurus April 20 GEM Gemini May 21 CAN Cancel June 21 LEO Leo July 23 VIR Virgo August 23 LIB Libra September 23 SCO Scorpio October 23 SAG Sagittarius November 22 CAP Capricorn December 22 AQU Aquarius January 20 PIS Pisces February 19 To Date April 19 May 20 June 20 July 22 August 22 September 22 October 22 November 21 December 21 January 19 February 18 March 20 Welcome to SIM Set Theory lesson 8: Properties of set 1. Union example 2. Intersection example 3. Subset example 4. Difference example 5. Complement example 6. Sets equality example 7. Distributive Law 1 8. Distributive Law 2 9. Quit Your option: 0 When you enter option 0, you will see the following interactions: 4 Your option: 0 Here is an example of set A = {LEO, PIS, SAG, ARI} All elements in set are distinct and random order Some basic operations in set 1. Add an element 2. Check an element 3. Cardinality 4. Zodiac Info format 9: Quit Enter your option: 1 Enter an element: LIB A = {LEO, PIS, SAG, ARI, LIB} A set is generated and is displayed. You can now try a few simple set operations, add an element, belong to operation, display the cardinal number and a display in enum format. Note that the sub-menu is repeated after each operation. Let us enter the option 1 in the submenu, Some basic operations in set 1. Add an element 2. Check an element 3. Cardinality 4. Zodiac Info format 9: Quit Enter your option: 1 Enter an element: ARI A = {LEO, PIS, SAG, ARI, LIB} You can see in the above two interactions, adding an element which is already inside the set, the final set remains unchanged; otherwise, this distinct element is added to the set. Let us explore option 2 5 Some basic operations in set 1. Add an element 2. Check an element 3. Cardinality 4. Zodiac Info format 9: Quit Enter your option: 2 Enter an element: PIS Element PIS is in set For option 3, the system just simply displays the cardinal number: Some basic operations in set 1. Add an element 2. Check an element 3. Cardinality 4. Zodiac Info format 9: Quit Enter your option: 3 No of elements in set is 5 For option = 4: Some basic operations in set 1. Add an element 2. Check an element 3. Cardinality 4. Zodiac Info format 9: Quit Enter your option: 4 Notation in enum format A = {Leo, Pisces, Sagittarius, Aries, Libra} The system invokes another format (enum format) of display method. You can continue to stay in the submenu or enter 9 to go back to the main menu. Let us choose 9 to go back to the main screen to test other operations. 6 Let us now explore each of the options in the main menu: (Note that the main menu is also repeated) In the main menu, you choose option 1: Welcome to SIM Set Theory lesson 0: Properties of set 1. Union example 2. Intersection example 3. Subset example 4. Difference example 5. Complement example 6. Sets equality example 7. Distributive Law 1 8. Distributive Law 2 9. Quit Your option: 1 Given sets A = {SCO, PIS} B = {LEO, GEM, SCO, PIS, LIB} Union of A and B = {SCO, PIS, LEO, GEM, LIB} In option 1, the system randomly generates two sets and displays the union of these two sets. The same is done for option 2, but evaluate the intersection of the two sets: 7 Welcome to SIM Set Theory lesson 0: Properties of set 1. Union example 2. Intersection example 3. Subset example 4. Difference example 5. Complement example 6. Sets equality example 7. Distributive Law 1 8. Distributive Law 2 9. Quit Your option: 2 Given sets A = {LIB, ARI, VIR, TAU, CAN, AQU, CAP, SCO, GEM} B = {GEM, VIR, PIS, CAP, SAG, LEO, ARI, CAN} Intersection of A and B = {ARI, VIR, CAN, CAP, GEM} Important to note, main menu is always displayed. In the following screen shot, you see the notation of an empty set. Your option: 2 Given sets A = {VIR, LEO} B = {ARI, GEM, CAP} Intersection of A and B = {} For option 3, the subset operation: Your option: 3 Given sets A = {ARI, AQU, TAU, CAP, LEO, VIR, PIS, GEM, SCO, CAN, LIB} B = {TAU, ARI, PIS, VIR, CAN, CAP, LEO, SAG, SCO, LIB, GEM, AQU} Conclusion A subset of B: true B subset of A: false For option 4, the difference of two sets: 8 Your option: 4 Given sets A = {AQU, SAG, SCO, VIR, CAN, LEO} B = {PIS, SAG, SCO, LEO, LIB, CAP} A B={AQU, VIR, CAN} Now, option 5, the complement of a set is done with the universal set. Our universal set is the set of zodiac signs. The following shows some of the interactions and displays: Your option: 5 Given set A = {PIS, CAP, LIB, ARI, LEO, TAU, CAN} A' = {GEM, VIR, SCO, SAG, AQU} Option 6 is the set equality. The following shows some of the possible interactions and display: Your option: 6 Given sets Analysis A = {ARI, GEM, CAN, LEO, TAU} B = {ARI, CAN, LEO, GEM, TAU} A subset of B: true B subset of A: true Conclusion A equals to B: true Your option: 6 Given sets Analysis A = {LEO, VIR, PIS, CAN, TAU, SAG} B = {CAP, PIS, SAG, VIR, TAU, GEM, SCO, ARI, LEO, AQU, CAN} A subset of B: true B subset of A: false Conclusion A equals to B: false 9