Often in engineering you need to find the roots (zeroes) of polynomial functions. You should know how to do this for linear and quadratic functions, but there is no generalized analytic method for higher order polynomials. In general, the roots are computed numerically. A typical root finding algorithm is the Newton-Raphson (Newton) method.

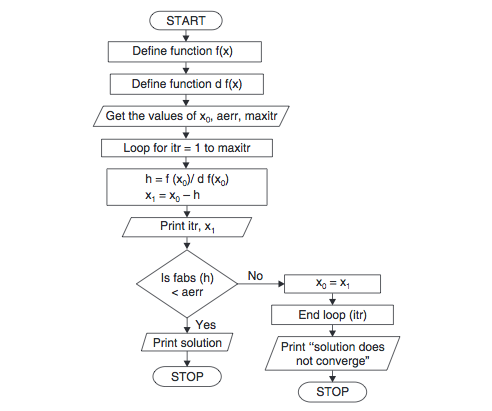
A flow chart is shown in Figure 1.

Figure 1- Flow Chart Newton-Raphson Root Finding Method

As an overview, for a given polynomial function, compute its first derivative analytically. To start the root finding process, specify a tolerance () and an initial guess (x0).

An improved estimate for the actual root can be computed as:

x1=x0+x=x0-f(x0)f'(x0)

Where f(x) is the polynomial and f'(x) is its 1st derivative. Continue to compute improved estimates for the root until the condition:

xn-xn-1

is satisfied at nth iteration of the loop.

For this exercise, you need to implement the Newton method to find the roots of the polynomial:

fx=x4+2x3-31x2-32x+60

This polynomial has all real, distinct roots (how many?) located in the range [-10, 10]. In addition to main(), you must write 3 functions to call the Newton method, compute the polynomial and its first derivative:

f'x=4x3+6x2-62x-32

Include and use the following constant variable in your program for your tolerance value.

const double TOLERANCE = .001;

Function prototypes should look like:

• double newtonRoot(double); // root finder

• double f(double); // f(x)

• double fprime(double); // f(x)

To find all the roots you will need to enter multiple guesses. In main(), allow the user to input as many initial guesses (x0) as the user wishes. For each guess call your newtonRoot() function to determine a root of the equation. Output the value of the root from main(). Each guess should be in the range of -10 to 10. Allow the user to exit the program when the user has finished guessing. Keep guessing until you find all the roots The program should run very quick!

Sample Program Run 1:

Enter Guess: -7

Root: -6

Enter Another Guess: y? y

Enter Guess: -8

Root -6

Enter Another Guess y? n

Near the top of main(), include the statements: cout.precision(4); and cout.setf(ios::fixed); to set the number of decimal places for the output.

You will also need to include the library header files: #include and #include . In c++, the absolute value is computed using the fabs()function call which is in .

START Define function f(x) Define function d f(x) Get the values of xo, aerr, maxitr Loop for itr-1 to maxitr haf(x)/ d f(%) Print itr, x s fabs (h)No XoX1 End loop (itr) Print "solution does