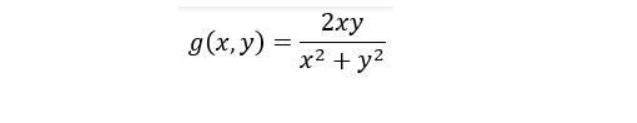
q) Present the numerical value of the double integral ff G(x, y)dydr. r) Explain how we know that the level curve g(x, y) = 0 exists. s) Explain how the existence of the above level curve influences the accuracy of approximating g(x, y) by its second-degree Taylor polynomial. t) Comment on the use of polynomial approximations of two-variable functions as a method of approximating integration of two-variable functions. g(x, y) = = 2xy x + y