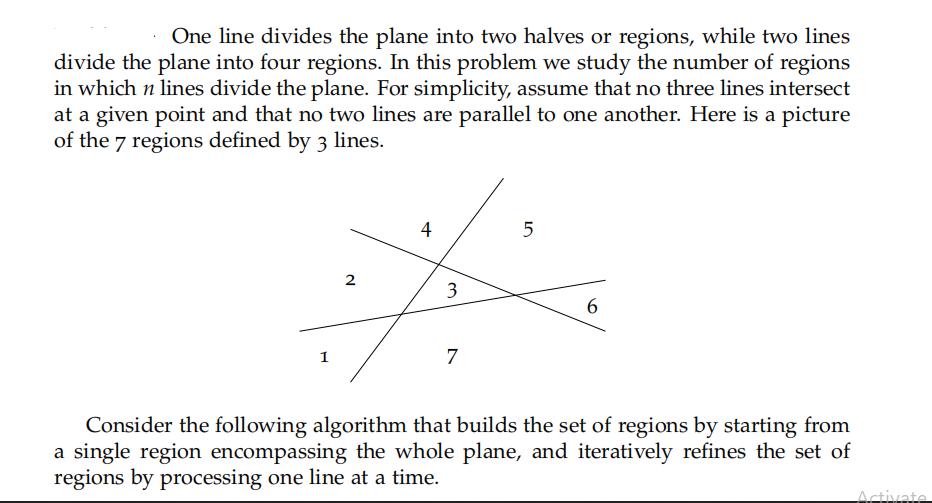
One line divides the plane into two halves or regions, while two lines divide the plane into four regions. In this problem we study the number of regions in which n lines divide the plane. For simplicity, assume that no three lines intersect at a given point and that no two lines are parallel to one another. Here is a picture of the 7 regions defined by 3 lines. 5 4 2 3 1 7 6 Consider the following algorithm that builds the set of regions by starting from a single region encompassing the whole plane, and iteratively refines the set of regions by processing one line at a time. Activate 1: function BUILD ARRANGEMENT (lines) [new region spanning whole plane] lines do for region regions do if line intersects region then Append region to old 2: 3: regions for line 4: old[] 5: new [] 6: 7: 8: 9: 10: 11: 12: 13: 14: 15: 16: return regions left, right split region through line Append left to new Append right to new for xold do Remove x from regions for x = new do Append x to regions a) Prove that at the beginning of the ith iteration of the for loop in Line 3 the line cuts through exactly i regions from the previous iteration. b) Prove that at the end of the ith iteration of the for loop in Line 3 2+1+2 regions. Remember to use the fact that no three lines intersect in the same point! we have