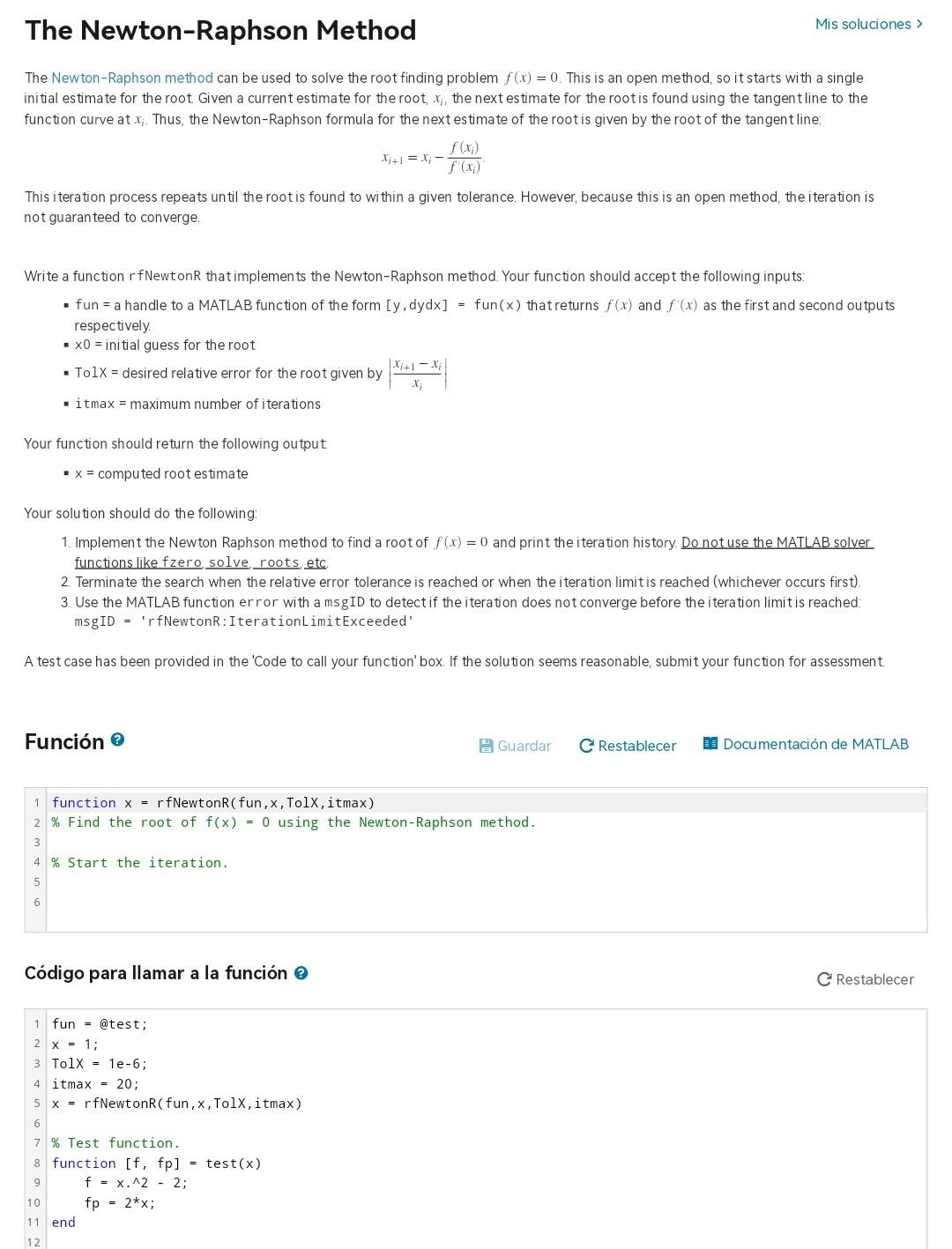
Only Matlab please

The Newton-Raphson method can be used to solve the root finding problem f(x)=0. This is an open method, so it starts with a single initial estimate for the root. Given a current estimate for the root, xi, the next estimate for the root is found using the tangent line to the function curve at xi. Thus, the Newton-Raphson formula for the next estimate of the root is given by the root of the tangent line: xi+1=xif(xi)f(xi). This iteration process repeats until the root is found to within a given tolerance. However, because this is an open method, the iteration is not guaranteed to converge. Write a function r fNewtonR that implemen ts the Newton-Raphson method. Your function should accept the following inputs: - fun = a handle to a MATLAB function of the form [y,dydx]=fun(x) that returns f(x) and f(x) as the first and second outputs respectively. - x0= initial guess for the root - Tol = desired relative error for the root given by xixi+1xi - itmax = maximum number of iterations Your function should return the following output - x= computed root estimate Your solution should do the following: 1. Implement the Newton Raphson method to find a root of f(x)=0 and print the iteration history. Do not use the MATLAB solver functions like fzero, solve roots, etc. 2. Terminate the search when the relative error tolerance is reached or when the iteration limit is reached (whichever occurs first). 3. Use the MATLAB function error with a msgID to detect if the iteration does not converge before the iteration limit is reached: msgID= 'rfNewtonR:IterationLimitExceeded' A test case has been provided in the 'Code to call your function' box. If the solution seems reasonable, submit your function for assessment. Funcin 0 function x=rf fewtonR(fun, x, TolX, itmax) \% Find the root of f(x)=0 using the Newton-Raphson method. C Restablecer